-
车内低频噪声的预测与控制是当前车内降噪研究的一个热点[1-6].然而,现有车内低频噪声的预测及控制方法,多通过结构、声腔的耦合模型计算出车内声压,针对超出目标值的峰值声压,进行板块声压贡献分析、声压灵敏度分析等,综合计算分析结果提出改进措施,以降低车内噪声[7-9].这些方法往往需要进行大量计算,并且锁定薄弱局部结构有一定难度,要获得满意的降噪效果,一般需要多次重复同类型的分析计算工作,耗费很多时间和人力,在工程应用中逐渐表现出弱势,故有必要开展车内低频噪声的快速控制方法研究.
前期提出一种基于声压幅度判定参数的车身低噪声设计方法[10-11],是在详细分析任意形状封闭腔内声压计算公式的基础上得到,然而研究并未对影响腔内声压的关键因素进一步展开探讨.并且也未见基于腔内声压计算公式深入分析模态参数、尺寸参数等对腔内声压影响规律的文献[12-15],而这些是进行结构内部声压快速有效控制的重要前提.
鉴于此,拟首先找到腔内声压可直接用公式计算的研究对象及其腔内声压的计算公式,然后基于该腔内声压的计算公式,分析公式中的可变输入量,找出影响腔内声压的主要模态参数、尺寸参数,采用仅改变某一参数而保持其余参数为初始值的方法,逐个分析这些参数对腔内声压的影响规律,以期找出影响腔内声压的关键参数及其影响规律并进行试验验证;最后将找出的关键参数及其影响规律用于某型轿车的车内低频噪声控制中,分析其在车内低频噪声控制中的应用效果.
HTML
-
综合前期研究结果及查阅大量资料发现,若要直接用公式计算某耦合系统的腔内声压,则要求该耦合系统的结构和声腔的固有频率和固有振型均可直接用公式计算.然而,符合这样要求的耦合系统非常有限,图 1为含一个弹性面的简单长方体结构声腔耦合系统,是其中具有代表性的一个,因此选定该耦合系统为研究对象.
图 1所示耦合系统的物理参数如下:声腔的边长分别是lax=1.0 m,lay=0.6 m,laz=0.5 m;弹性钢板的边长分别是lsx=1.0 m,lsy=0.6 m,钢板厚度hs=1.2 mm.激励力Fs=10 N;激励力作用点xf=0.3 m,yf=0.2 m;声腔内响应点xr=0.7 m,yr=0.4 m,zr=0.4 m(更多激励点和响应点的计算结果表明,所得规律一致,故仅展示此结果).
该耦合系统的腔内声压计算公式[14]为
式中:ρ0为常温下空气密度;c0为常温下空气中的声速;Fs为激励力;ρs为结构密度;Va为声腔体积;n为声腔的模态阶次;p为结构的模态阶次;an为声腔振型形状系数;Fnp为频率重叠系数;Cnp为振型耦合系数;ω为激励力的圆频率;ωn为声腔固有频率;ωp为结构固有频率;ηa为粘性介质的损失因子;ηs为结构损失因子;φn为声腔振型;φp为结构振型.将结构和声腔的各阶固有频率、各阶固有振型的具体数值带入上述公式后,再将其余参数带入即可计算出腔内声压.
观察公式(1),(2),(3)发现,可变输入量可分成如下两类:求和符号前的结构板厚、声腔深度、耦合面积等3个尺寸参数;求和符号内的结构和声腔的固有频率、固有振型等4个模态参数,此7个参数即是腔内声压的主要影响参数.为了清楚掌握这7个参数对腔内声压的影响规律,逐一计算仅改变某一参数,而其余参数取初始值时的腔内声压,通过分析腔内声压的变化情况,讨论各个参数对腔内声压的影响规律.
-
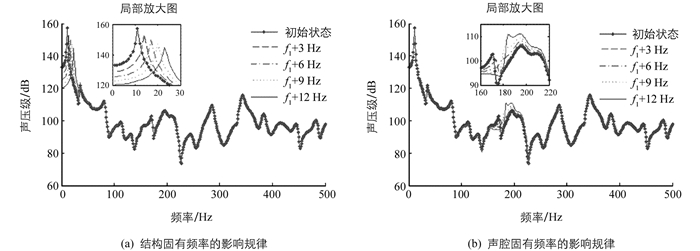
分别计算了结构第一阶固有频率和声腔第一阶非零固有频率从初始值开始逐步增加至12 Hz时,耦合系统的腔内声压,结果如图 2.
从图 2中曲线发现:
1) 结构固有频率逐步增加时,对应的峰值声压向高频移动,声压大小逐步降低,如图 2(a)所示.
2) 声腔固有频率逐步增加时,对应的峰值声压向高频移动,并逐渐与附近的峰值声压融合为一个较宽的峰值,融合后的峰值声压呈升高趋势,如图 2(b)所示.
3) 上述两种情况下,除对应的峰值声压会移频外,其余声压均几乎没有变化.
计算更多阶结构和声腔的固有频率逐步改变后的腔内声压,结果表明腔内声压的变化规律类似,即峰值声压移频,其余声压几乎不变,所以不再展开讨论.
综上所述,改变固有频率,仅仅起到峰值声压的移频作用,而不能实现消除峰值声压的目的,故通常不建议从频率角度研究腔内声压的控制措施.
-
图 1所示耦合系统的结构和声腔的固有振型,有如下计算公式[14]:
式中:n1、n2、n3是非负整数,代表各阶声腔振型在各条边上的节线数,即各阶声腔振型中相对变形为零的点连接而成的线的条数;p1、p2是正整数,代表各阶结构振型在各条边上的节线数,即各阶结构振型中相对变形为零的点连接而成的线的条数.将公式(4),(5)带入公式(1),(3)化简消去x、y后,可变输入量变为节线数.因此,讨论结构、声腔的固有振型对腔内声压的影响规律,改变为讨论结构、声腔固有振型的节线数对腔内声压的影响规律.
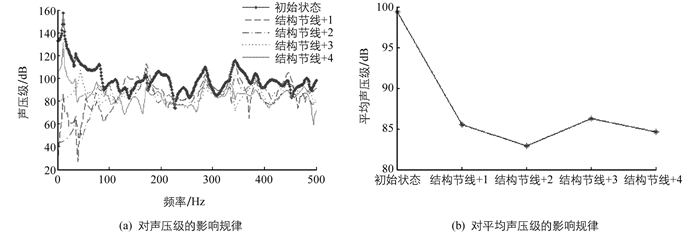
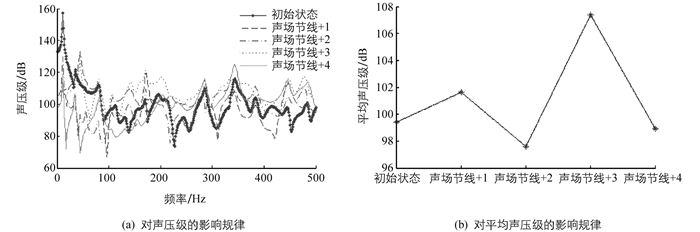
分别计算了仅结构和仅声腔的各阶振型的节线数从初始值开始逐步增加1~4条时(相当于实物添加“+”加强筋或加强梁,节线数+1代表增加一个“+”加强筋或加强梁),耦合系统的腔内声压级和平均声压级,结果绘于图 3和图 4中.
1) 观察图 3中曲线发现:结构振型的节线数逐步增加时,声压级变化明显,平均声压级呈降低趋势.当增加1条节线时,声压级和平均声压级均显著降低;增加2条时,声压级和平均声压级不再进一步明显降低,而100 Hz内峰值声压的个数减少;增加3条时,声压级和平均声压级略有回升,而100 Hz内声压升高,高于100 Hz的降低;增加4条时,声压级和平均声压级略有降低,而100 Hz内声压进一步升高,高于100 Hz的进一步降低.因此,增加结构振型的节线数会降低腔内声压,但并不是节线数增加得越多越好,增加1条节线便能有效降低腔内声压,并且增加1条节线,即增加1个“+”加强筋或加强梁,亦便于在物理结构中实现.
2) 观察图 4中曲线发现:声腔振型的节线数逐步增加时,声压级变化也明显,平均声压级时升时降.当增加1条节线时,声压级和平均声压级有升高;增加2条时,声压级和平均声压级降低,而100 Hz内声压降低,高于100 Hz的声压与初始状态在同一水平;增加3条时,声压级和平均声压级升高,且高于初始状态;增加4条时,声压级和平均声压级回降,与初始状态在同一水平,而100 Hz内声压低于初始状态,高于100 Hz的声压高于初始状态.所以,增加声腔振型的节线数难以降低腔内声压,且在实际结构中也很难实现(虽然在物理声腔中布置吸声材料可获得近似零声压区域,但吸声材料对低频声几乎没有作用),故一般不建议从声腔振型的节线数角度研究腔内声压的控制措施.
-
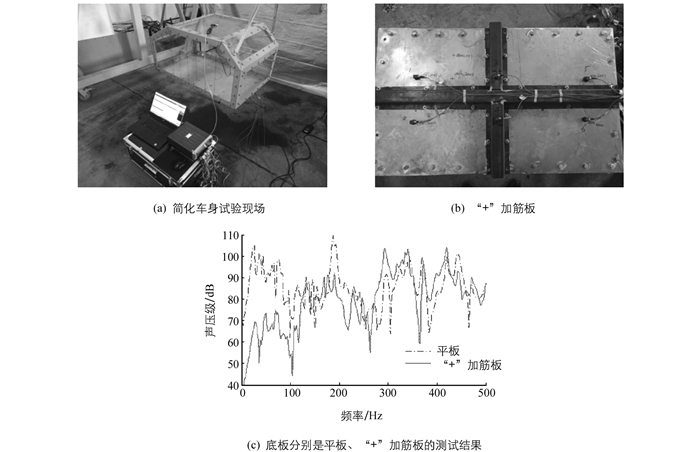
搭建一简化车身的试验平台,如图 5(a)所示,用于验证“结构振型增加1条节线便能有效降低声压”这一结论.试验样车的骨架采用角钢;封闭声腔的各个面,除底面外,均采用板厚10 mm的有机玻璃;底面是可拆卸的弹性钢板,分别制作了平板、“+”加筋板各一张,作为可更换底板,如图 5(b).
测试了底板分别安装平板、“+”加筋板两种情况下,样车内部的声压,试验结果绘于图 5(c),其中激励采用力锤,响应点采用传声器测量.观察图 5(c)中曲线发现:
1) 平板添加“+”加强筋后,200 Hz以内的低频声压有明显降低,这与图 3(a)的结果一致,从而验证了“结构振型增加1条节线便能有效降低腔内声压”这一结论.
2) 虽然试验结果是底板的结构改变,从而振型和频率同时改变而形成的腔内声压,但是前文研究发现频率改变只能使峰值声压移频,而无法降低声压,且图 5(c)的结果与图 3(a)的结果一致性很好,更进一步说明振型的节线数对声压影响更明显,所以可仅从结构振型的节线数角度提出腔内声压的控制措施.
2.1. 固有频率
2.2. 固有振型
2.3. 试验验证
-
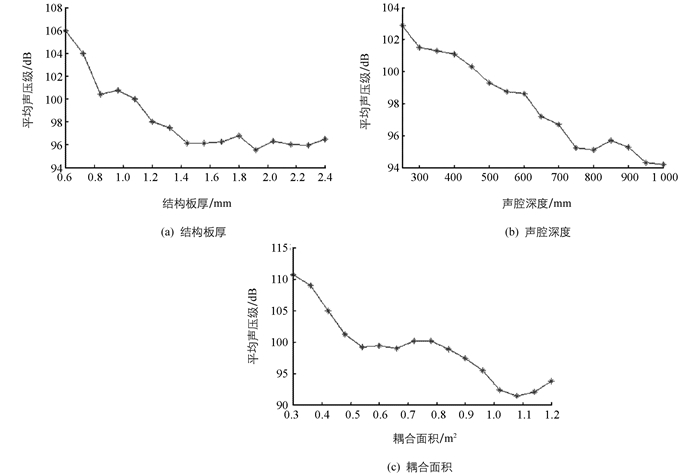
分别计算了结构板厚、声腔深度、耦合面积从初始值的0.5倍逐步增加到2倍时,耦合系统的腔内平均声压级(因从诸工况的声压级曲线未发现明显规律,故计算平均声压级),结果绘于图 6中.观察图 6中曲线发现:
1) 随着结构板厚的增加,平均声压级呈降低趋势,如图 6(a)所示.若要降低腔内声压,可根据实际情况,增加结构板厚.
2) 随着声腔深度的增加,平均声压级呈降低趋势,如图 6(b)所示.虽然增加声腔深度,可降低腔内声压,但需考虑物理空间是否允许,且通常情况下实车上无足够大可调整空间,所以一般不建议采用该措施.
3) 随着耦合面积的增加,平均声压级整体呈现降低趋势,如图 6(c)所示.因同样需要考虑物理空间是否允许,故一般也不建议采用该措施.
-
依据前文研究结果,提出车内低频噪声快速控制的一条新思路:
1) 找出车身结构主要贡献模态;
2) 以“结构增加一个‘+’加强筋或加强梁、或增加结构板厚”为指导,对车身结构提出改进措施,而不再需要进行板块声压贡献分析、声压灵敏度分析等.以下将新思路应用于某型车的车内低频噪声控制中,分析研究结论的应用效果.
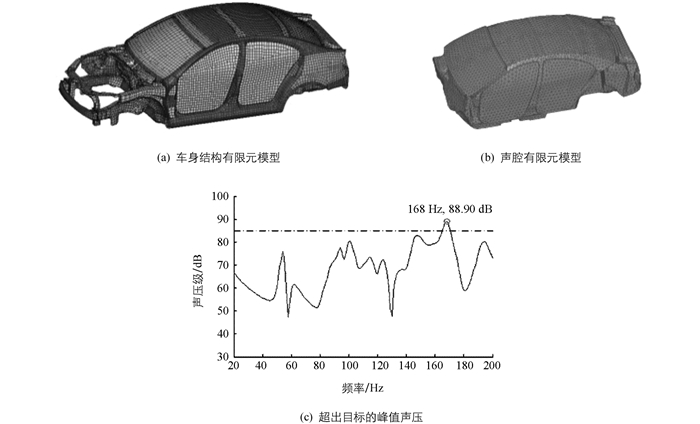
建立某三厢车的车身结构有限元模型、声腔有限元模型如图 7(a),(b)所示.篇幅所限,两个有限元模型的建模细节及实验验证请见文献[16].计算了原车在单位激励下的车内声压,图 7(c)中展示的是激励点为发动机右悬置、响应点为驾驶员右耳的结果.该型车在单位激励下的声压目标是在0~200 Hz范围内不超过85 dB,则原车在168 Hz上出现超出目标的峰值声压,如图 7(c)中标识.经过分析发现第十五阶、第十六阶车身结构模态是168 Hz对应峰值声压的主要贡献模态,它们在耦合面上的振型分量如图 8所示,可见这2阶模态的振型幅值较大区域主要分布在右侧和左侧车门区域.
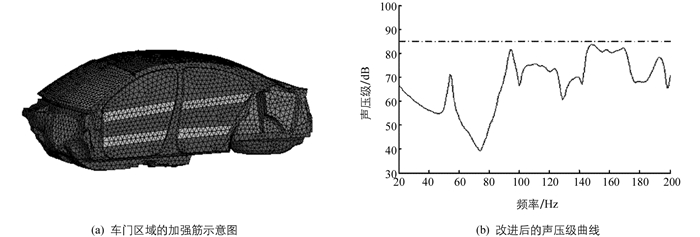
针对主要贡献模态,提出车身结构改进措施:在第十五阶、第十六阶车身结构模态的振型幅值较大区域“增加1个‘+’加强筋或加强梁”,但因车门上方是玻璃,故将“+”加强筋,调整为“二”加强筋,如图 9(a)所示.进一步计算结构调整后的车内声压,激励点和测点与图 7(c)一致的结果,如图 9(b)所示,可见原超出目标的峰值声压降低了约10dB,且所有声压全部在目标曲线以下,车内低频噪声得到快速、有效控制.可见前文研究结果应用效果较好,为车内低频噪声的快速控制提供了一条新思路.
-
基于长方体结构声腔耦合系统的腔内声压计算公式,分析模态参数、尺寸参数等与腔内声压的关系,找出了关键参数及其影响规律,并将它应用到某型车的车内低频噪声控制中,主要结论如下:
1) 封闭腔内声压的关键参数是结构振型的节线数、结构板厚;并且增加1条节线,即增加1个“+”加强筋或加强梁,或增加结构板厚,可有效降低腔内低频声压.
2) 因物理空间限制或降噪效果不明显,不建议从结构固有频率、声腔固有频率、声腔振型的节线数、声腔深度、耦合面积等参数角度提出改进措施.
3) 研究结果在某型轿车的车内低频噪声控制中的应用效果表明,与通过板件声压贡献分析、声压灵敏度分析等进行声压控制相比,依据本文研究结论能够更快速、有效地降低声压.








 DownLoad:
DownLoad: