Study on the Influence of Maturation Delay on Spread of Wolbachia in Mosquito Population

文献[12]建立了如下数学模型描述Wolbachia在蚊子种群中的传播：

其中：I(t)表示被Wolbachia感染的蚊子数量，U(t)表示未被Wolbachia感染的蚊子数量；β∈[0, 1]是垂直传播的可能性；q∈[0, 1]是CI影响的可能性；b＞0是出生率；d＞0是死亡率；D≥0是适合度损失. 模型(1)考虑了Wolbachia的垂直传播和CI两种影响，由文献[3]可知，对于某种特定的Wolbachia菌株，其垂直传播率和CI影响发生的可能性都近似接近1，也即，如果雌性蚊子感染了Wolbachia，其后代也会感染；正常雌性蚊子与感染雄性蚊子的后代会因为发生CI而死亡. 所以，我们假设β=1，q=1，并忽略掉适合度的影响(D=0).蚊子的一生有4个阶段(卵、幼虫、蛹、成虫)，从卵到成虫大约需要14~21 d，雌性蚊子的寿命约3个月，故蚊子的成熟时间不能被忽略，此因素可用成熟时滞描述. 而成熟时滞又受季节性影响，故考虑为周期时间依赖的时滞，记为τ(t). 根据文献[13]的方法，将τ(t)引入模型(1)中得到如下模型：

其中：δ为幼年蚊子的死亡率，e^-δτ(t)是幼年蚊子成熟的可能性. τ(t)是[0，+∞)上的非负、有界且连续可微的ω-周期函数，满足0≤τ(t)≤τ，常数τ=$\mathop {\sup }\limits_{t \ge 0}${τ(t)}，τ≥0；μ(t)和ν(t)是关于t∈[-τ，0]的正连续函数.

首先引入如下定义：令χ：=C([-τ，0]，$\mathbb{R}^{2}$)，且具有最大模. 如果函数x(·)∈C([-τ，∞]，$\mathbb{R}^{2}$)，则x_t∈χ可被定义为x_t(θ)=x(t+θ)，∀θ∈[-τ，0]. 对任意ϕ∈χ，定义f(t，ϕ)=(f₁(t，ϕ)，f₂(t，ϕ))，其中

因为τ(t)是ω-周期的，故有f(t+ω，ϕ)=f(t，ϕ). 所以，模型(2)是一个ω-周期泛函微分系统.

假设g(t)是一个连续的ω-周期函数，令

则对于系统(2)解的适定性有如下结果.

引理1  对任意ϕ=(ϕ₁，ϕ₂)∈χ₊：=C([-τ，0]，$\mathbb{R}_+^{2}$)，系统(2)在[0，∞)上有唯一的非负有界解S(t，ϕ)(S₀=ϕ).

证  在χ₊的每个紧子集上，f(t，ϕ)关于ϕ是连续且Lipschitz的. 所以，对任意ϕ∈χ₊，系统(2)在其最大存在区间上有唯一的具有初值S₀=ϕ的解S(t，ϕ).

定义b_c=(1-τ′(t))e^-δτ(t)b. 由系统(2)可知：

我们令

则有

易知

又令

并由

可得到

再令

对任意给定的ρ≥1，令

则[0，ρx^*]_χ是关于χ的有序区间.

容易证明：对任意ψ∈[0，ρx^*]_χ(ψ_i(0)=0~(ψ_i(0)=ρx_i^*)，i=1，2)和t∈$\mathbb{R}$，有f_i(t，ψ)≥0~(f_i(t，ψ)≤0). 进一步地，[0，ρx^*]_χ对于系统(2)是正不变的. 通过选择任意大的ρ即可得到解关于χ₊的正性和有界性. 证毕.

定理1  系统(2)有一个种群灭绝平衡态(0，0)，且是不稳定的.

证  (0，0)的存在性容易得到，此略去. 定义Y(t)=(I(t)，U(t))为系统(2)的任意解，且|Y(t)|=$\sqrt{I_{(t)}^{2}+U_{(t)}^{2}}$. 对于t∈[t₀-τ，t₀]，Y(t)=Φ(t). 定义Φ(t)的范数为||Φ||=sup{|Φ(t)|：t₀-τ≤t≤t₀}.

假设(0，0)是稳定的. 则对任意ε＞0，存在δ=δ(t₀，ε)＞0使得|Y(t)|＜ε对于任意的t≥t₀和Φ(t)(||Φ||≤δ)成立. 令Y(t)是系统(2)满足I₀=inf{I(t)：t₀-τ≤t≤t₀}＞0的解，则I₀≤δ. 下一步，我们将证明I(t)＞$\frac{I_{0}}{2}$对所有的t≥t₀成立.

假设对任意t≥t₀，I(t)＞$\frac{I_{0}}{2}$不成立. 则存在一个t₁＞t₀使得对于t∈[t₀-τ，t₁)有I(t)＞$\frac{I_{0}}{2}$和I(t₁)=$\frac{I_{0}}{2}$. 所以，I′(t₁)≤0. 由系统(2)的第一个方程知：

由于|Y(t)|＜ε，则有I(t₁)＜ε和U(t₁)＜ε. 所以，

我们取

则有

故对任意的t≥t₀，有I(t)＞$\frac{I_{0}}{2}$成立，矛盾. 所以(0，0)是不稳定的. 证毕.

因为τ(t)∈[0，τ]，所以，我们首先分析常数时滞的情况. 令τ(t)=r，系统(2)存在如下两个非平凡平衡态(I^*，U^*)：

下分析E₁和E₂稳定性，将系统(2)在(I^*，U^*)处线性化后可写为

其中x(t)=(I(t)，U(t))^T且

这里

且有

假设系统(2)具有形如x(t)=c e^λt(c≠0)的解，则可得到系统(3)的特征方程如下：

展开得

其中：a¹，a²分别为矩阵A的第一列和第二列；b¹，b²分别为矩阵B的第一列和第二列.

可以计算得到

则在E₁=(0，$\frac{\mathrm{e}^{-\delta r} b}{d}$)处，特征方程为

由特征根的符号易知E₁是不稳定的.

在E₂=($\frac{\mathrm{e}^{-\delta r} b}{d}$，0)处，特征方程为

易知E₂是渐近稳定的.

综上可得如下结果：

定理2  在区域{(I，U)：I，U≥0}中，当τ(t)=r时，系统(2)有两个非平凡平衡态E₁和E₂，且E₁是不稳定的，E₂是局部渐近稳定的.

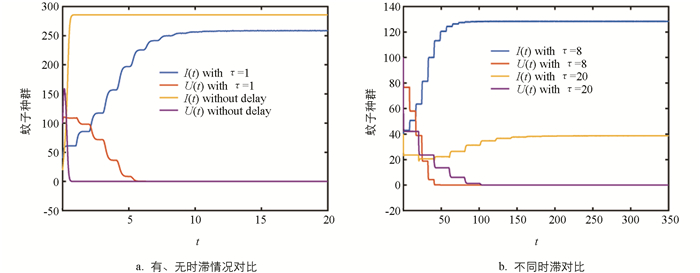
由定理2可知：如果垂直传播是完全的，Wolbachia最终将完全入侵蚊子种群. 图 1a将系统(2)在有时滞((μ(t)，ν(t))=(20，100))和无时滞((I₀，U₀)=(20，100))两种情况下的动力学行为做了比较，比较结果见表 1. 表 1说明：无时滞的ODE系统将高估蚊子总量，这对蚊子种群的控制是不利的，因此成熟时滞对于蚊子种群的动力学行为有重要影响.

图 1b将不同时滞对系统(2)动力学行为的影响做了对比. 可以看出：时滞越小，系统(2)解趋于稳定的时间越短，也即，如果环境有利于蚊子的成熟，Wolbachia完全入侵蚊子种群的速度会加快. 但从蚊子总量看，相比于大时滞，小时滞会使环境中有更多的蚊子. 在实际中，我们应该寻找平衡这两种互反影响的方法.

当成熟时滞是周期函数τ(t)时，我们将通过数值模拟讨论时滞对系统(2)动力学行为的影响. 根据广州市的登革热数据，拟合出成熟时滞表达式为：

其中

并且

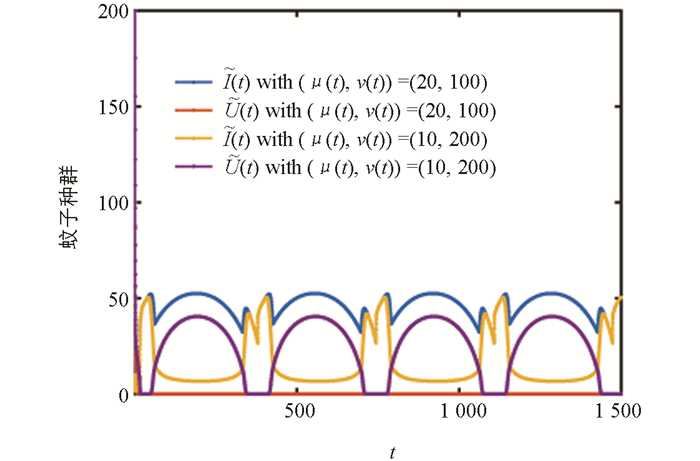
图 2显示了不同历史值对系统(2)周期解的影响. 可以看出：(μ(t)，ν(t))=(20，100)时，正常蚊子种群将会灭绝；(μ(t)，ν(t))=(10，200)时，正常蚊子种群与携带Wolbachia的蚊子种群共存，并呈现周期波动. 从取值来看，当携带Wolbachia的蚊子种群在历史值中所占比例较大时，Wolbachia会完全入侵野生蚊子种群.

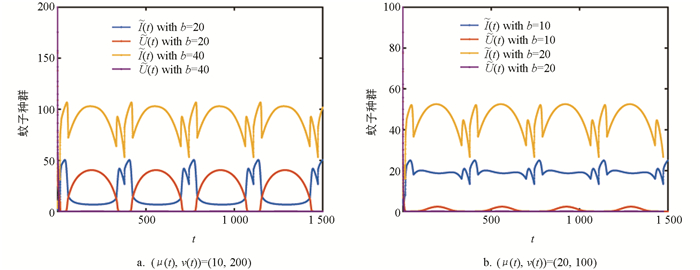
图 3在图 2历史值的基础上，研究了不同出生率对系统(2)周期解的影响. 图 3a中(μ(t)，ν(t))=(10，200)，当b=20时两种蚊子种群共存，当b=40时正常蚊子种群灭绝，图 3b中(μ(t)，ν(t))=(20，100)，当b=10时两种蚊子种群共存，当b=20时正常蚊子种群灭绝，说明出生率越大，越有利于Wolbachia的传播.

本文主要研究成熟时滞对Wolbachia传播的影响. 研究发现：①对于常数时滞，时滞越大越有利于疾病的控制；②携带Wolbachia的蚊子种群在历史值中所占比例越大，越有利于Wolbachia的传播；③蚊子种群出生率越大，越有利于Wolbachia的传播.