Dynamic Behavior of High Order Nonlinear Fuzzy Difference Equation

定义 1^[11]  u称为模糊数，如果$u: \mathbb{R} \longrightarrow[0, 1]$满足条件

1) u是正规的，即存在x为实数，使得u(x)=1；

2) u是模糊凸的，即对所有的t∈[0, 1]，x₁，x₂∈ $\mathbb{R}$有

3) u是上半连续的；

4) u的支撑集是紧集，即是$\operatorname{supp} u=\overline{\bigcup_{\alpha \in(0, 1)}[u]_{\alpha}}=\overline{\{x: u(x)>0\}}$是紧集.

对于所有的α∈(0，1]，u的α-截集表示为[u]_α={x∈$\mathbb{R}$：u(x)≥α}.

定义 2^[11]  设u，v是正模糊数，则u，v的α-截集表示为[u]_α=[u_l，α，u_r，α]，[v]_α=[v_l，α，v_r，α]，α∈(0，1]，且

定义u的模为

u，v之间的距离为D(u，v)，其中

引理 1^[11]  设连续函数g：$\mathbb{R}^+$×$\mathbb{R}^+$×$\mathbb{R}^+$→$\mathbb{R}^+$，对于任意正模糊数u，v，ω以及∀α∈(0，1]，都有

定义 3^[11]  令u，v是模糊数，α-截集为[u]_α=[u_l，α，u_r，α]，[v]_α=[v_l，α，v_r，α]，0∉[v]_α，对于∀α∈(0，1]，定义÷_g(g-除法)：存在一个模糊数ω，且[ω]_α=[ω_l，α，ω_r，α]，使得

即是

易知，任意的模糊数u，当u定义在g-除法上时，有u÷_gu=1，当u定义在Zadeh扩展原则上时，u÷_gu≠1.

引理 2^[11]  令u，v都是模糊数，如果ω=u÷_gv存在，则有以下两种情况.

1) 若∀α∈[0, 1]，都有u_l，αv_r，α≤u_r，αv_l，α，则ω_l，α= $=\frac{u_{l, \alpha}}{v_{l, \alpha}}$，ω_r，α= $=\frac{u_{r, \alpha}}{v_{r, \alpha}}$，

2) 若∀α∈[0, 1]，都有u_l，αv_r，α≥u_r，αv_l，α，则ω_l，α= $\frac{u_{r, \alpha}}{v_{r, \alpha}}$，ω_r，α= $\frac{u_{l, \alpha}}{v_{l, \alpha}}$.

引理 3^[13]  令u，v，ω都是正模糊数，∀α∈(0，1]，如果ω=u÷_gv满足引理2中的1)，则

如果ω=u÷_gv满足引理2中2)，则

因此有

注  因为|u_r，αv_r，α-u_l，αv_l，α|≥|u_r，αv_l，α-u_l，αv_r，α|，由(3)，(4)，(5)式可知，运用g-除法优于Zadeh扩展原则.

引理 4^[13]  考虑差分方程

其中：n=0，1，2，…，m；m∈$\mathbb{N}^{+}$，α，β，y_i(i=-m，…，-1，0)都是正实数. 则

1)  方程

有一正一负的两个实特征根λ₁，λ₂.

2)  对方程(7)的每一个正解，都有$\lim\limits_{n \rightarrow \infty} y_{n}=\max \left\{\lambda_{1}, \lambda_{2}\right\}$.

定义 4^[11]  令y=max{λ₁，λ₂}，其中λ_i(i=1，2)是(7)式的特征根，则称y为(6)式的唯一平衡点.

引理 5^[13]  考虑差分方程系统

其中m为正整数，α，β，μ，ν，y_i，z_i(i=-m，…，-1，0)都是正实数. 则有

1)  方程

有两个一正一负的实特征根λ₁，λ₂(或γ₁，γ₂).

2)  方程(9)的每一个正解，都有

定义 5^[4]  令y=max{λ₁，λ₂}，z=max{γ₁，γ₂}，其中λ_i，γ_i(i=1，2)是方程(9)的特征根，则称(y，z)是方程(8)的唯一解.

定义 6^[4]  设{x_n}是正模糊数数列，若存在正实数P，Q，使得

则称(x_n)是有界且持久的.

定义 7^[11]  如果正模糊数数列(x_n)满足模糊差分方程(1)，则称x_n是方程(1)的正解. 如果x满足方程

则称x是模糊差分方程(1)的平衡点.

定义 8^[4]  (x_n)是正模糊数数列，x是模糊数，如果$\lim\limits _{n \rightarrow \infty} D\left(x_{n}, x\right)=0$，则称当n→∞时x_n→x.

主要对两个模糊数运用g-除法，讨论高阶非线性模糊差分方程

解的唯一性以及全局渐进行为. 其中m为正整数，A，B，x_i(i=-m，…，0)都是正模糊数.

定理 1  令A，B，x_i(i=-m，…，0)都是正模糊数，且$\frac{B}{A}$，$\frac{B}{x_{i}}(i=-m, \cdots, 0)$满足引理2中的1)，则(10)式存在唯一正解x_n.

证  定理的证明与文献[15]中的命题3.1的证明类似，这里省略定理1的证明.

定理 2  令A，B，x_i(i=0，1，…，m)都是正模糊数，且$\frac{B}{A}$，$\frac{B}{x_{i}}(i=-m, \cdots, 0)$满足引理2中的2)，当不等式

成立时，(10)式存在唯一解x_n.

注  定理2的证明方法与定理1基本一致.

定理 3  考虑差分方程(6)，存在一个正常数θ＞0，当n≥1时，有

证  由(6)式可知，对于∀α≥1，都有y_n≥α. 当n→∞时，则有

其中

所以有

同理可得

因此，对于∀n≥m，都有

其中

由(6)式及(13)式，可得

定理证明完毕.

定理 4  考虑方程(10)，其中A，B以及初始条件x_i(i=-m，…，0)都是正模糊数，当方程(10)中除法满足引理2中的1)时，方程(10)的每一个正解x_n都是有界持久的.

证  因为A，B以及初始条件x_i(i=-m，…，0)都是正模糊数，所以存在M_i，N_i(i=0，1，2，3，…，m)使得

令x_n是方程(10)中满足引理2中1)情形时的正解，由定理3及方程(10)，则有

其中

联系(15)式，可得

由(15)，(16)式可得到L_n，α≥P，其中

同理得

因此，对于n≥1，有

也即是

由定义6知，x_n是有界持久的. 证毕.

定理 5  考虑差分方程系统

其中m为正整数，α，β，μ，ν，y_i，z_i(i=-m，…，0)都是正实数，当不等式组

成立时，存在正常数K₁，K₂，C₁，C₂，使得

证  由引理5可知，系统(17)存在唯一正解(y_n，z_n)，且易得出y_n≥α，z_n≥μ，当n→∞时，由(17)式有

所以有

同理可得

其中$\delta_{1}=\frac{\beta}{\alpha \mu+\nu}$，由(18)，(19)，(20)式可得

其中

同理可得，当$\frac{\nu}{\alpha \mu+\beta}<1$时，有y_n＜C₂，其中

令$K_{1}=\alpha+\frac{\beta}{C_{2}}$，$C_{1}=\mu+\frac{\nu}{K_{2}}$，则有K₁≤y_n≤K₂，C₁≤z_n≤C₂. 证毕.

定理 6  若$\frac{B_{r, \alpha}}{A_{l, \alpha} A_{r, \alpha}+B_{l, \alpha}}<1$，则当方程(10)中g-除法满足定理2中2)时，则方程(10)的解是有界且持久的.

证  令方程(10)的解为x_n，因为$\frac{B_{l, \alpha}}{A_{l, \alpha} A_{r, \alpha}+B_{r, \alpha}}<\frac{B_{r, \alpha}}{A_{l, \alpha} A_{r, \alpha}+B_{l, \alpha}}<1$，由于方程(10)的g-除法满足定理2中2)，所以有

对于L_n，α，R_n，α，由定理5以及(22)式有

其中

由(15)式有

再令

即P≤L_n，α，同理可得Q≤ R_n，α，其中

所以，当n≥1时，有$\bigcup\limits_{\alpha \in(0, 1]}\left[L_{n, \alpha}, R_{n, \alpha}\right] \subset[P, Q]$，即是$\overline{\bigcup\limits_{\alpha \in(0, 1]}\left[L_{n, \alpha}, R_{n, \alpha}\right]} \subseteq[P, Q]$. 定理证毕.

定理 7  当方程(10)中的g-除法满足引理2中1)时，则

1)  方程(10)存在唯一平衡点x；

2)  当n→∞时，方程(10)每一个正解x_n都趋于唯一平衡点x.

证  由引理2中1)与(10)式可得

由(23)式对应方程为L_α²-A_l，αL_α-B_l，α=0及$\mathbb{R}_{\alpha}^{2}-A_{r, \alpha} R_{\alpha}-B_{r, \alpha}=0$，得特征根为

由引理4、(23)式和(24)式可知

由(15)，(25)式有

由(24)，(25)，(26)式可知$\bigcup\limits_{\alpha \in(0, 1]}\left[L_{\alpha}, R_{\alpha}\right] \subset[m, n]$，则$\overline {\bigcup\limits_{\alpha \in (0, 1]} {\left[ {{L_\alpha }, {R_\alpha }} \right]} } $是紧集，且$\overline {\bigcup\limits_{\alpha \in (0, 1]} {\left[ {{L_\alpha }, {R_\alpha }} \right]} } \subset (0, \infty )$，由[L_α，R_α]确定的一个模糊数x使得

且x是方程(10)的正平衡点. 接下来证明唯一性. 假设方程(10)存在另外一个平衡点x，则有

并且

由(23)，(28)式可知L_α= $\overline {{L_\alpha }} $，R_α= $\overline {{R_\alpha }} $，也即是x =x，唯一性成立. 由(25)式有

也即x_n→x. 定理证毕.

定理 8  当方程(10)中的g-除法满足定理2中2)情形时，则有以下结论成立

1)  方程(10)存在唯一平衡点x；

2)  方程(10)每一个正解x_n都趋近于唯一平衡点x.

注  定理8证明与定理7相似，此处省略定理8的证明.

例 1  考虑四阶模糊差分方程

其中：A，B以及初值x_i(i=-3，-2，-1，0)如下

取α-截集，有

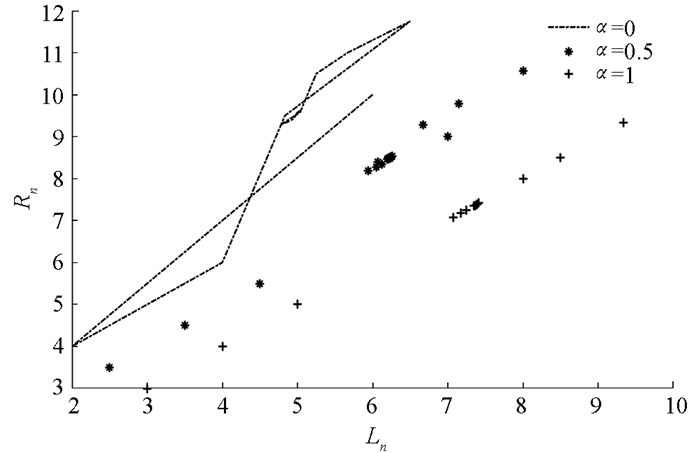
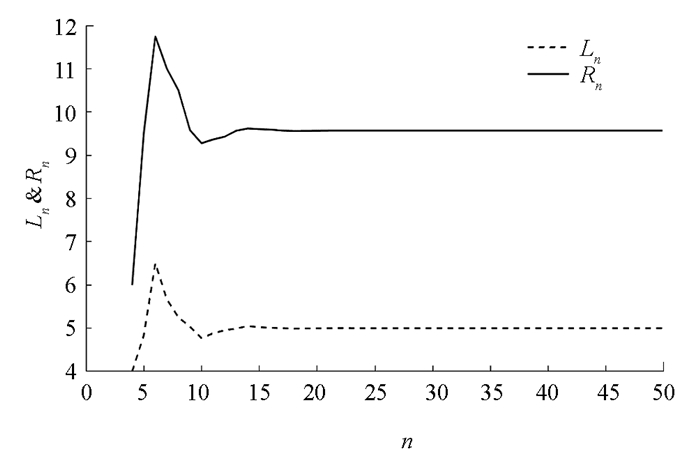
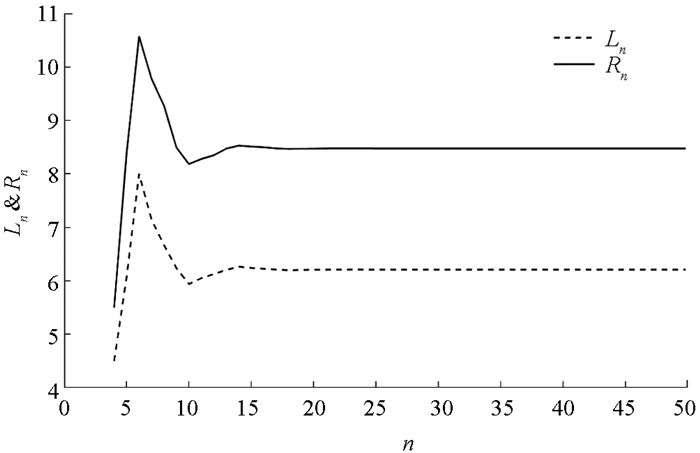
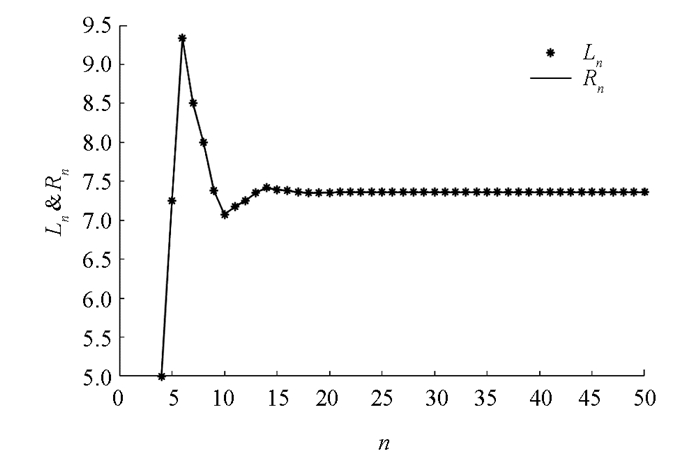
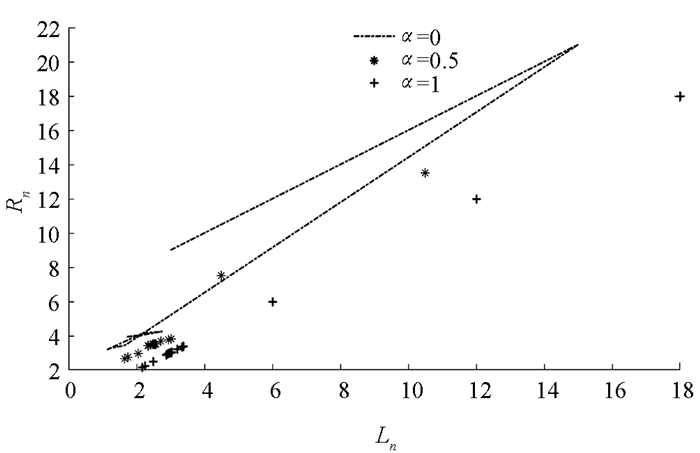
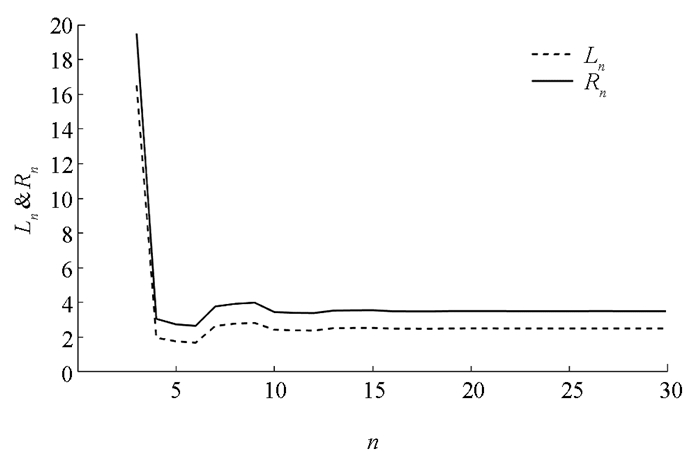
因此，$\frac{B}{A}$，$\frac{B}{x_{i}}(i=-3, -2, -1, 0)$满足引理2中的1)，因此有

由定理4可知，方程(29)的解都是有界持久的，且存在唯一平衡点x，当n→∞时，方程(29)的每一个正解x_n都收敛于唯一平衡点x(如图 1-4).

例 2  考虑三阶模糊差分方程

其中A，B以及初值x_i(i=-2，-1，0)如下

所以有

由此可知，$\frac{B}{A}$，$\frac{B}{x_{i}}(i=-2, -1, 0)$满足引理2中的2)，且

因此

由定理6可知，(29)式的解都是有界持久的，且由定理8可知，方程(31)存在唯一平衡点x，当n→∞时，方程(31)的每一个正解x_n都收敛于唯一平衡点x (如图 5-8).

本文主要运用g-除法，研究在两种情况下高阶非线性模糊差分方程(1)的正解存在性以及唯一性，有界性以及持久性以及解的渐近行为. 结论得出，方程(10)的每一个正解都趋近于唯一平衡点，最后分别给出三阶和四阶符合条件的数值例子，更好验证结论的有效性.