Multi-Objective Optimization of Muffler Noise and Back Pressure Based on Surrogate Model

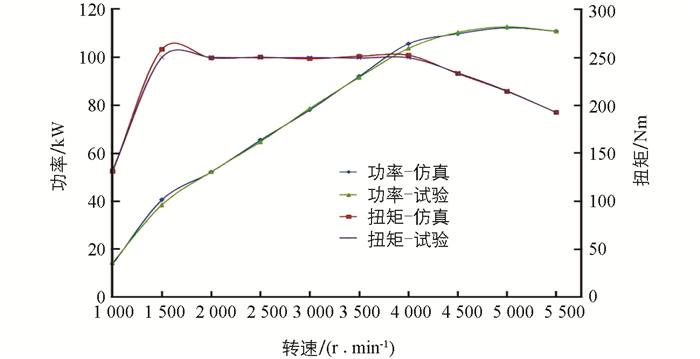
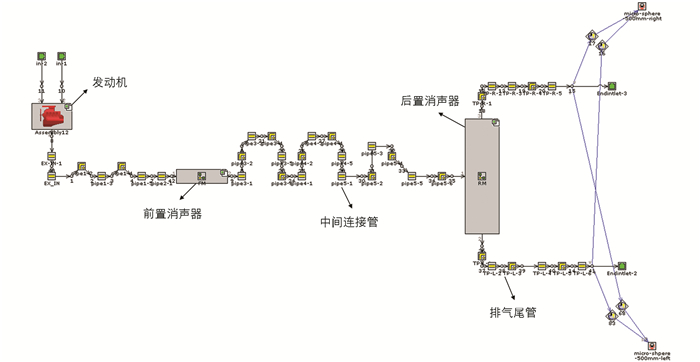
根据表 1发动机参数信息，利用GT-PWOER软件建立发动机一维仿真模型，应用发动机台架试验结果对一维模型进行标定. 输出功率和扭矩与台架试验结果对比如图 1所示. 仿真功率最大误差在4 000 r/min时为2.8%，仿真扭矩最大误差在1 500 r/min时为3.4%，最大误差均小于5%，说明该发动机仿真模型比较精确，可以用于排气系统尾管噪声分析.

对图 2所示初始消声器在GT-POWER中建立对应的消声器GEM3D模型并与发动机模型耦合，如图 3所示.

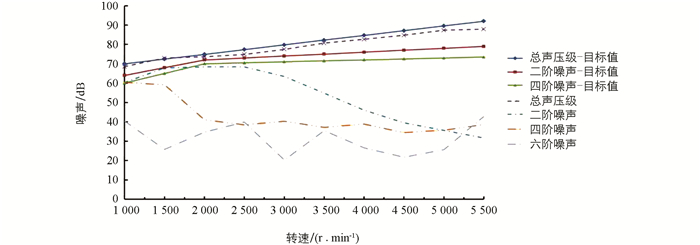
选择10个转速工况(图 4)，分析各工况的尾管噪声总声压级. 在排气消声器设计时，为了使整车定置噪声达到法规要求，除了应使排气尾管噪声总值低于限值要求外，通常还需要对排气声品质进行调节，一般通过限制各阶次噪声的方法来实现，因此提取尾管噪声2，4，6阶次噪声并与目标限值进行比较.

由图 4可知，初始方案尾管噪声除了在1 500 r/min时稍稍超过目标限值，其他转速下尾管噪声均在目标限值以内，且二阶噪声起主要作用.

排气系统的面网格选择三角形单元，为了使生成的体网格更加精细，隔板穿孔位置单元尺寸设置为1.5 mm，其它面网格尺寸设置为3 mm，面网格划分完成后检查网格封闭性和单元质量，网格中不能存在自由边，最小单元角度不能小于1°，最小单元尺寸应大于0.1 mm. 最后将合格的面网格以.stl格式导入到STAR-CCM+中，设置3层边界层，增长率为1.2，进出口网格设置为拉伸体网格，长度为100 mm，层数设置30层. 体网格类型为多面体网格，总计生成3 576 622个体单元.

进口设置质量流量边界条件，质量流量为0.139 kg/s，温度设置为850 ℃，数据为台架试验测得. 湍流强度为0.03，湍流长度尺度设为0.004 5. 尾管出口为压力出口边界条件，温度为300 K，壁面边界为无滑移边界条件，载体壁面为绝热边界条件，其余壁面为对流换热边界条件，换热系数为30 W/m²·k，环境温度为300 K. 最大求解步数为2 000步，结合设置的求解监视器和残差曲线判断求解是否收敛.

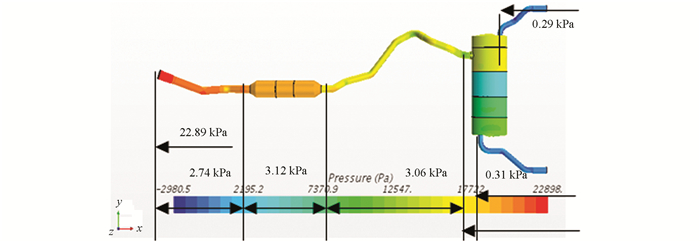
迭代求解达到收敛以后，得到排气系统初始方案压力场结果如图 5所示. 可以看出，整个排气系统压力分布由进口到出口逐渐降低，前消和后消压力损失分别为3.12 kPa和13.97 kPa. 前消进口背压为22.89 kPa，大于背压目标限值20 kPa，排气系统背压需要进行优化.

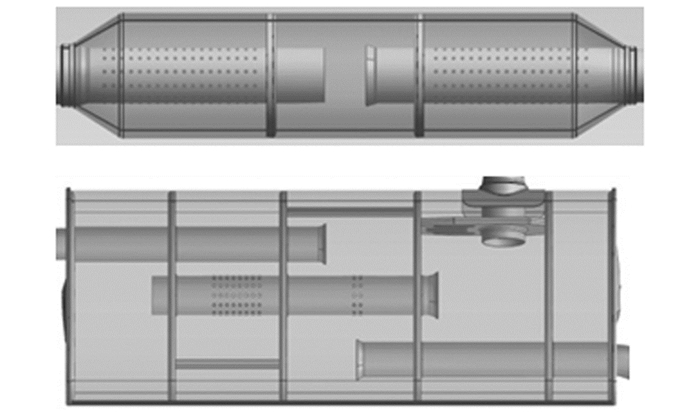
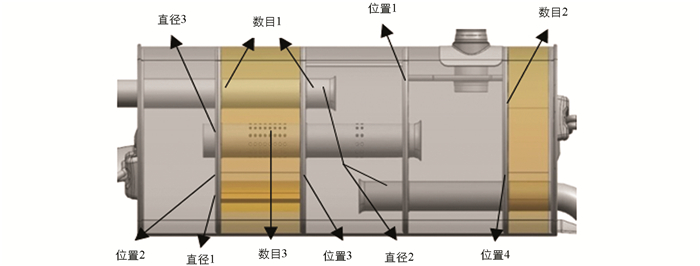
对消声器优化时选取了10个优化变量，分别对应隔板穿孔直径、隔板穿孔数、穿孔管的穿孔数、3个芯管的直径以及4个隔板的位置，如图 6所示.

由于初始方案尾管噪声除了1 500 r/min超过目标限值外，其他转速均符合噪声要求，并且要求整个排气系统在5 500 r/min(额定转速)时前消进口背压小于20 kPa，因此将1 500 r/min的尾管噪声和5 500 r/min的背压作为优化目标. 同时消声器容积不可能无限制增大，且穿孔管与穿孔板的穿孔率也不能超过30%，否则消声性能会急剧变差^[8]，因此设置如下优化目标式(1)和约束条件式(2)：

优化目标：

约束条件：

随着工程问题复杂程度的增加，仿真模型越来越复杂、规模越来越大，求解耗时成倍增加，直接将多目标优化算法应用到具有物理意义的实际仿真模型将耗费大量资源，因此迫切需要引入高效多目标优化方法^[9]. 基于代理模型的多目标优化方法是通过重新构建目标与对应变量间的数学关系的代理模型以逼近真实模型，然后在代理模型上应用多目标优化算法进行优化，从而大幅提高优化效率.

代理模型是通过插值或拟合的方式来建立输入量和输出量的关系. 为保证代理模型的精度和效率，构建代理模型时包括两个重要内容，首先通过试验设计采集构建代理模型所需的样本点，然后进行试验设计样本点的拟合与模型精度验证^[10].

确定了优化变量的取值范围以及优化目标后，利用试验设计方法进行代理模型样本点的采集. 最优拉丁超立方(OLHD)是在拉丁超立方(LHD)的基础上增加了优化准则(常用的优化准则有熵、极大极小距离、总均方差和中心化偏差)，能同时满足设计变量的投影均匀性和设计空间分布均匀性^[11]. 本文选择最优拉丁超立方试验设计进行优化变量采样，总共采集了80组试验样本(表 3).

Isight多学科优化设计软件提供的近似模型包括响应面模型(Response Surface，RSM)、径向基神经网络模型(Radial Basic Function Neural Network)、克里金模型(Kriging)3种. 通过用最优拉丁超立方采样方法采集80组样本，50组样本用于构建代理模型，30组用于检验代理模型精度. 对构建的3种代理模型的误差分析结果如表 4所示.

代理模型常见的误差评价指标为R²，计算公式如式(3)，由表 4可知，响应面模型和径向基神经网络模型的排气背压R²值均小于0.9，误差精度不合格，而Kriging模型的尾管噪声和排气背压R²值均大于0.9，说明Kriging模型可作为消声器多目标优化模型.

式中，f_i，$ \widetilde{f_i}$，$ \overline{f_i}$分别为测试点响应的真实值、近似值、真实响应的平均值，n_t为测试代理模型精度的样本点个数. R²越接近于1，意味着代理模型精度越好，一般认为R²＞0.9时建立的代理模型是可靠的^[12].

应用已建立的Kriging模型，结合带有精英保留策略的非支配排序遗传算法(NSGA-Ⅱ)^[13]对消声器进行尾管噪声和背压的多目标优化，优化算法参数设置如表 5.

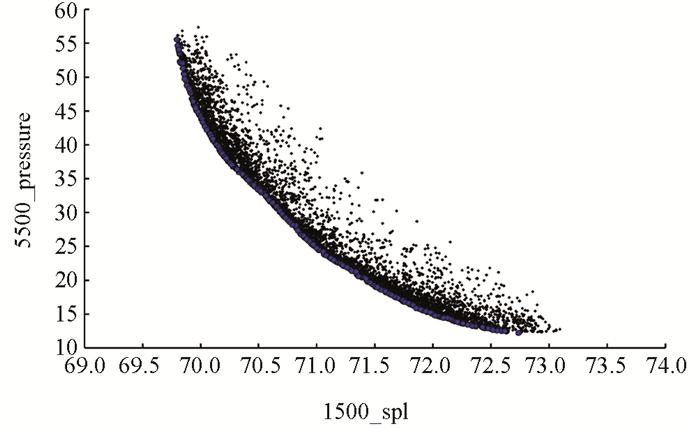
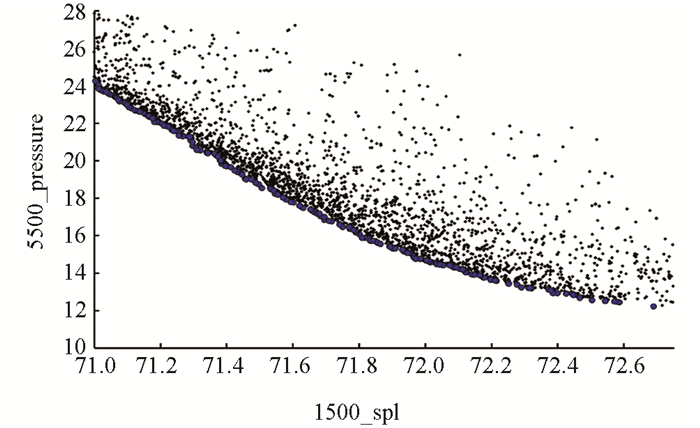
多目标优化问题可以有很多全局最优解，不存在唯一最优解. 目前普遍采用Pareto定义，即在满足约束的前提下，对任何一个子目标的进一步改进必然使至少一个其他子目标变差，该点就被称为Pareto最优点. 一个多目标优化问题通常有许多Pareto点，所有这些点构成多目标优化问题的Pareto前沿，对于两设计目标，Pareto前沿可由一条曲线表达. 而NSGA-Ⅱ算法显著改善了Pareto前沿解的多样性和算法鲁棒性，经过6 000步进化寻优后得到最终的Pareto前沿(图 7)和局部放大(图 8).

Pareto前沿是一个解集，在Pareto前沿上的解为一组非支配解，需要根据所关注的目标选择一个折衷的多目标优化解. 根据5 500 r/min时整个排气系统背压要小于目标限值20 kPa和1 500 r/min时尾管噪声越低越好的要求，在Pareto前沿背压小于20 kPa附近选择一个设计空间作为最终的多目标优化解，将多目标优化后的结果与优化前仿真结果进行对比(表 6).

由表 6可知，应用代理模型多目标优化后，1 500 r/min时尾管噪声由72.9 dB(A)减小到71.5 dB(A)，减小了1.4 dB(A). 排气系统背压由22.89 kPa减小到19.65 kPa，减小了3.24 kPa. 将代理模型优化得到的最优变量值代入实际模型进行验证，尾管噪声和排气背压分别与实际模型结果相差0.2 dB(A)和0.02 kPa，误差分别为0.3%和0.1%，说明代理模型多目标优化可行，多目标优化后尾管噪声和背压符合消声器开发设计要求.

为验证实际仿真模型和代理模型优化结果的可行性，用试验对优化方案的声学性能和背压进行验证. 台架试验参照汽车排气消声器总成技术条件和试验方法执行^[14]，背压测点位置与仿真输出相同，试验与仿真结果如图 9和图 10所示.

根据图 9可知，尾管噪声仿真值与试验结果吻合较好，各个转速下的误差均在2%以内. 图 10显示，额定转速(5 500 r/min)时排气背压试验值为19.8 kPa，仿真值与试验值相差仅为0.86%，说明该代理模型得到的结果可行，优化后的消声器尾管噪声和排气背压达到了开发设计要求.

本文通过仿真和试验相结合的方法对消声器进行尾管噪声和排气背压多目标优化，主要结论如下：

1) 采用最优拉丁超立方试验设计方法采集样本点，构建了多目标优化模型. 选取隔板穿孔直径、隔板穿孔数目、穿孔管的穿孔数目、3个芯管的直径以及4个隔板位置等10个参数为优化变量，设定1 500 r/min的尾管噪声和5 500 r/min的排气背压为优化目标.

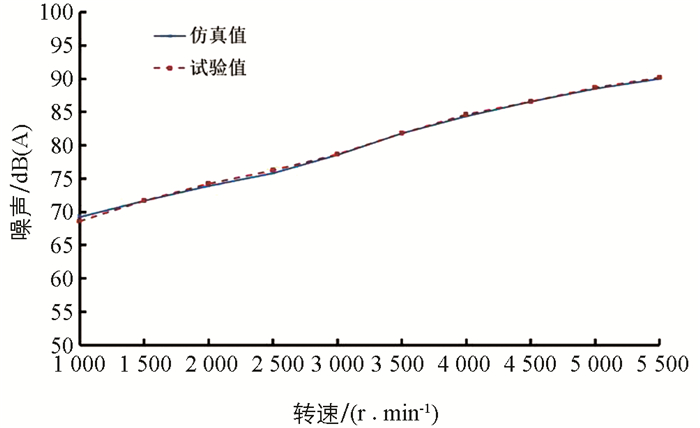
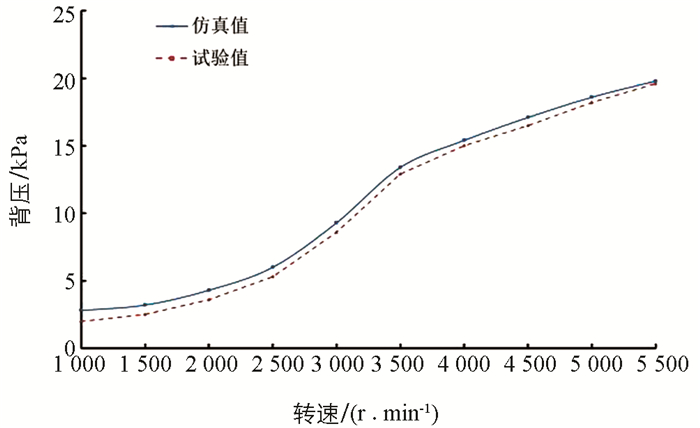
2) 鉴于流固耦合实际模型的复杂性，优化时选择精度最高的Kriging代理模型并结合NSGA-Ⅱ多目标优化算法对尾管噪声和背压进行多目标优化. 代理模型优化后尾管噪声仿真值与试验值误差均在2%以内. 额定转速(5 500 r/min)时排气背压试验值为19.8 kPa，小于20 kPa目标限值要求，仿真值与试验值相差仅为0.86%，消声器噪声和背压多目标优化达到了开发设计要求.