Incomplete Multi-Scale Decision System with Mixed Semantics and Its Optimal Scale Selection

本节主要介绍基于特征关系的不完备信息系统以及基于容差关系的不完备多尺度信息系统的基本概念.

定义1 ^[8]   信息系统S可以表示为一个二元组(U，A)，其中U={x₁，x₂，…，x_n}是一个非空有限对象集，称为论域; A={a₁，a₂，…，a_m}是一个非空有限属性集，对于任意的a∈A，满足a：U→V_a即a(x)∈V_a，x∈U，其中V_a={a(x)|x∈U}称为a的值域. [(a，v)]为属性-值对(a，v)的块，记：

定义2 ^[8]   S=(U，A)是一个不完备信息系统，V_a={a(x)|x∈U}为属性a∈A的值域. 符号“*”和“ $ \mathit{\emptyset} $ ”分别表示遗漏和缺席型未知属性值. 对于属性-值对的块[(a，v)]，有：①若a(x)=*，则x∈[(a，v)]; ②若a(x)=$ \mathit{\emptyset} $，则$x \notin[(a, v)] $. 其中$ \forall x \in U, a \in B \subseteq A$，记：

K(x，a)为x关于属性a的不可分辨对象集，则特征集K_B(x)定义为：

对于∀x，y∈U，特征关系R_B为U上关于属性子集B $ \subseteq $ A的广义不可分辨关系，记：

显然，特征关系R_B仅满足自反性，而不一定满足对称性和传递性. 若IIS中的所有未知属性值都是遗漏型，则特征关系R_B退化为容差关系^[7]; 若IIS中的所有未知属性值都是缺席型，则特征关系R_B退化为相似关系^[6]. 因此，可以将特征关系看作是容差关系和相似关系的一种泛化表现形式.

设(U，A)是一个不完备信息系统，$\forall X \subseteq U, B \subseteq A$，则X关于特征关系R_B的上近似集和下近似集分别定义为

根据X关于R_B的上、下近似集，可将论域U划分为3个互不相交的区域，分别为正域、边界域及负域，定义为

POS(X)表示一定属于X的对象集，NEG(X)表示一定不属于X的对象集，BND(X)表示不确定是否属于X的对象集. X关于R_B的近似精度定义为：

其中|X|表示集合X的基数. X关于R_B的粗糙度定义为：

定义3 ^[14]    S=(U，A)是一个多尺度信息系统，其中U={x₁，x₂，…，x_n}为论域，A={a₁，a₂，…，a_m}是一个非空有限属性集，且每个属性都是多尺度属性. 假设所有属性都有I个相同的尺度级数，则多尺度信息系统可以表示为(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})，其中，a_j^k：U→V_j^k，V_j^k是属性a_j在第k个尺度的值域，对于j=1，2，…，m，k=1，2，…，I-1，存在满射函数g_j^k，k+1：V_j^k→V_j^k+1使得a_j^k+1=g_j^k，k+1°a_j^k，即：

称g_j^k，k+1为粒信息转换函数. 对于k∈{1，2，…，I}，记$ A ^ k =\left \{ a _1^ k , a _2^ k , \cdots , a _ m ^ k \right \}$，则一个多尺度信息系统S=(U，A)可以分解为I个信息系统S^k=(U，$ A ^ k $)，k=1，2，…，I.

若S¹=(U，A¹)是一个不完备信息系统，则称(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})为不完备多尺度信息系统^[30]. 用符号“*”表示未知属性值，即如果a_j^k(x)=*，就认为x在属性a_j^k上的值是未知的. 此时不同尺度层次之间的属性值变换为：

其中，j=1，2，…，m; k=1，2，…，I-1; x∈U.

本节主要给出混合语义下的不完备多尺度信息系统的定义，并讨论数据填补和特征关系模型的扩展.

现有不完备多尺度信息系统的研究通过引入容差关系处理多尺度信息系统中的数据缺失，但只考虑了遗漏型未知属性值，并且认为多尺度信息系统S的不完备是由于S¹的不完备，因此对象x在多尺度属性a_j下缺失，则a_j¹(x)=a_j²(x)=…=a_j^I(x)=*，即x在a_j的所有尺度下全部缺失. 而在实际应用中，可能存在遗漏型和缺席型未知属性值共存于一个多尺度信息系统，并且对象x只是在多尺度属性的某些尺度下缺失. 因此，针对已有研究的不足，本小节将定义混合语义下的不完备多尺度信息系统.

定义4    多尺度信息系统中的某些属性值未知，并且未知属性值是两种语义的任意解释，则称该信息系统为混合语义下的不完备多尺度信息系统，仍表示为S=(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m}). 符号“*”和“ $ \mathit{\emptyset} $ ”分别表示遗漏和缺席型未知属性值，即若a_j^k(x)=*或a_j^k(x)=$ \mathit{\emptyset} $，则认为x在属性a_j^k上的值未知，否则x在属性a_j^k上的值已知.

例1    表 1是一个具有3个尺度和2个属性的混合语义下的不完备多尺度信息系统S=(U，A)=(U，{a_j^k|k=1，2，3，j=1，2})，其中，U={x₁，x₂，…，x₈}，A={a₁，a₂}. S同时具有遗漏和缺席型未知属性，对象在多尺度属性下存在全部缺失也存在部分缺失，如x₂在a₁下部分缺失，x₅在a₂下全部缺失.

定理1   (U，{a_j^k|k=1，2，…，I，j=1，2，…，m})是一个多尺度信息系统，存在粒信息转换函数g_j^k，k+1：V_j^k→V_j^k+1，k=1，2，…，I-1，对于∀x，y∈U：

1) a_j^k+1(x)=g_j^k，k+1(a_j^k(x));

2) a_j^k+1(x)≠a_j^k+1(y)→a_j^k(x)≠a_j^k(y);

3) a_j^k(x)=a_j^k(y)→a_j^k+1(x)=a_j^k+1(y).

在不完备多尺度信息系统中，对于在多尺度属性a_j上部分缺失的对象，如果该对象在a_j的粗尺度下未知，而在细尺度下已知，此时根据定理1的1)可以填补粗尺度下的属性值. 因此，下面基于粒信息转换函数给出数据填补方法.

定义5    S=(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})是混合语义下的不完备多尺度信息系统，g_j^k，+1：V_j^k→V_j^k+1是相对S完备的多尺度信息系统的粒信息转换函数. 对于k∈{1，2，…，I}，记$ A ^ k =\left \{ a _1^ k , a _2^ k , \cdots , a _ m ^ k \right \}$，S^k=(U，$ A ^ k $)，数据填补后的S^k记为S^k*，数据填补后的S记为S^*，由S^1*，S^2*，…，S^I*组成，其中S^1*=S¹.

对于k∈{1，2，…，I-1}，根据g_j^k，k+1及S^k*对S^k+1进行数据填补得到S^k+1*：∀x∈U，a_j^k∈$ A ^ k $，若a_j^k+1(x)=*∨a_j^k+1(x)=$ \mathit{\emptyset} $并且a_j^k(x)≠*∧a_j^k(x)≠$ \mathit{\emptyset} $，则对a_j^k+1(x)进行填补有a_j^k+1(x)=g_j^k+1(a_j^k(x)).

定理2  设S=(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})是一个混合语义下的不完备多尺度信息系统，a_j∈A，x∈U，对于数据填补后的S^*有：

1) 若a_j^k(x)=*或a_j^k(x)=$ \mathit{\emptyset} $，则有a_j^m(x)=*或a_j^m(x)=$ \mathit{\emptyset} $，m∈{1，2，…，k};

2) 若a_j^k(x)≠*且a_j^k(x)≠$ \mathit{\emptyset} $，则有a_j^m(x)≠*且a_j^m(x)≠$ \mathit{\emptyset} $，m∈{k，k+1，…，I};

3) 若x在a_j下部分缺失，即$\exists $ k∈{1，2，…，I-1}使得a_j^k(x)=*∨a_j^k(x)=$ \mathit{\emptyset} $而a_j^k+1(x)≠*∧a_j^k+1(x)≠$ \mathit{\emptyset} $，则有a_j^m(x)=*∨a_j^m(x)=$ \mathit{\emptyset} $，m∈{1，2，…，k}，并且a_jⁿ(x)≠*∧a_jⁿ(x)≠$ \mathit{\emptyset} $，n∈{k+1，k+2，…，I}.

例2    已知例1中S对应的完备多尺度信息系统的粒信息转换函数为：g₁^1，2(1)=g₁^1，2(2)=S，g₁^1，2(3)=M，g₁^1，2(4)=g₁^1，2(5)=L; g₁^2，3(S)=Y，g₁^2，3(M)=g₁^2，3(L)=N; g₂^1，2(1)=S，g₂^1，2(2)=g₂^1，2(3)=M，g₂^1，2(4)=g₂^1，2(5)=L; g₂^2，3(S)=N，g₂^2，3(M)=g₂^2，3(L)=Y.

对S进行数据填补：

根据g_j^1，2及S^1*=S¹对S²进行数据填补得到S^2*：a₁²(x₂)=$ \mathit{\emptyset} $并且a₁¹(x₂)=1，则a₁²(x₂)=g₁^1，2(1)=S;

根据g_j^2，3及S^2*对S³进行数据填补得到S^3*：a₁³(x₂)=$ \mathit{\emptyset} $并且a₁²(x₂)=S，则a₁³(x₂)=g₁^2，3(S)=Y; a₁³(x₆)=*并且a₁²(x₆)=M，则a₁³(x₆)=g₁^2，3(M)=N; a₂³(x₇)=$ \mathit{\emptyset} $并且a₂²(x₇)=L，则a₂³(x₇)=g₂^2，3(L)=Y.

由S^1*，S^2*，S^3*得到S^*，如表 2所示.

由于数据填补后可能仍然存在未知值，可以将特征关系引入数据填补后的不完备多尺度信息系统. 针对例2中数据填补后的S^*，根据公式2可得x₇关于属性子集{a₂}在不同尺度下的特征集：K_{a2¹}(x₇)=U，K_{a2²}(x₇)={x₃，x₆，x₇，x₈}，K_{a2³}(x₇)={x₂，x₄，x₆，x₇，x₈}. 显然不满足多尺度中尺度间的偏序关系K_{a2¹}$ \subseteq $K_{a2²}$ \subseteq $K_{a2³}.

观察表 2可以发现，在第2尺度下a₂²(x₇)与a₂²(x₁)，a₂²(x₂)，a₂²(x₄)不相等，在第3尺度下a₂³(x₇)与a₂³(x₃)不相等，由定理1知，在第1尺度下a₂¹(x₇)与a₂¹(x₁)，a₂¹(x₂)，a₂¹(x₃)，a₂¹(x₄)不相等; 因a₂²(x₅)=$ \mathit{\emptyset} $(不可比较)，则有x₅ $ \notin $ [(a₂²，L)]=K(x₇，a₂²)，而x₅∈K(x₇，a₂¹)，为满足尺度间的偏序关系，使得x₅$ \notin $K(x₇，a₂¹). 由此得到K_{a2¹}(x₇)={x₆，x₇，x₈}.

根据上述的分析，需要扩展特征关系模型以满足数据填补后混合语义下的不完备多尺度信息系统尺度间的偏序关系.

定义6   S=(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})是一个多尺度信息系统，[(a_j^k，v)]为属性-值对(a_j^k，v)的块，记：

定义7    S=(U，A)=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m})是一个混合语义下的不完备多尺度信息系统. 对于数据填补后的S^*，V_j^k={a_j^k(x)|x∈U}是属性a_j在第k个尺度的值域，对于属性-值对的块[(a_j^k，v)]，有：

1) 若a_j^k(x)=*，则x∈[(a_j^k，a_j^k(z))]，其中z∈U-Y，Y={y∈U|(m≠0∧a_j^m(x)≠a_j^m(y)，m=m_aj^k(x))∨($\exists $a_jⁿ(x)=$ \mathit{\emptyset} $，k＜n≤I)};

2) 若a_j^k(x)=$ \mathit{\emptyset} $，则x$ \notin $[(a_j^k，v)]，其中v∈V_j^k.

对于∀x∈U，k∈{1，2，…，I}，a_j∈B$ \subseteq $A，K(x，a_j^k)是x关于属性a_j^k的广义不可分辨对象集，定义如下：

1) 若a_j^k(x)≠$ \mathit{\emptyset} $且a_j^k(x)≠*，则

2) 若a_j^k(x)=$ \mathit{\emptyset} $或a_j^k(x)=*：

当a_j^I(x)=$ \mathit{\emptyset} $或a_j^I(x)=*时，

当a_j^I(x)≠$ \mathit{\emptyset} $且a_j^I(x)≠*时，

其中

m_aj^k(x)表示对象x在属性a_j的k尺度后属性值已知的最细尺度，若k尺度后属性值全部未知则m_aj^k(x)=0. 记：

K_B^k(x)是对象x关于属性集B在第k尺度下的特征集.

对于∀x，y∈U，k∈{1，2，…，I}，B$ \subseteq $A，特征关系$ R _{ B ^ k }$是S^*在第k尺度下由属性子集B导出的一个广义不可分辨关系：

对于x∈U，k∈{1，2，…，I-1}，混合语义下的不完备多尺度信息系统S^*的粒信息转换函数不是满射函数，仅当a_j^k(x)≠$ \mathit{\emptyset} $且a_j^k(x)≠*时，满足a_j^k+1(x)=g_j^k，k+1(a_j^k(x)). 一个混合语义下的不完备多尺度信息系统S^*可以分解为I个信息系统S^k*=(U，$ A ^ k $)，k=1，2，…，I.

例3  例2中数据填补后的S^*，由定义7可得到x₇关于B=A在不同尺度下的特征集，可得K_B¹(x₇)$ \subseteq $K_B²(x₇)$ \subseteq $K_B³(x₇).

定义8    S₁和S₂是非空集合U上的2个混合语义下的不完备多尺度信息系统，对于数据填补后的S₁^*和S₂^*分别有扩展后的特征关系R₁和R₂，若对于∀x∈U总有K_R1(x)$ \subseteq $K_R2(x)，那么就称U/R₁较U/R₂更细，或U/R₂较U/R₁更粗，记为U/R₁$ \subseteq $U/R₂.

定理3    $\left ( U , \left \{ A ^ k \mid k =1, 2, \cdots , I \right \}\right )$是一个混合语义下的不完备多尺度信息系统，对于数据填补后的$S^*, k=1, 2, \cdots I, B \subseteq A$，记：

如下性质成立：∀x∈U.

1) $R_{B^k}$是自反的，不一定是对称和传递的;

2) $R_{B^k}=\bigcap_{a \in B} R_{a^k}$;

3) 当$C \subseteq B \subseteq A$时, $R_{A^k} \subseteq R_{B^k} \subseteq R_{C^k}$;

4) 当$C \subseteq B \subseteq A$时, $K_{A^k}(x) \subseteq K_{B^k}(x) \subseteq K_{C^k}(x)$;

5) $R_{B^k} \subseteq R_{B^{k+1}}$，其中$k=1, 2, \cdots, I-1$;

6) $K_{B^k}(x) \subseteq K_{B^{k+1}}(x)$, 其中$k=1, 2, \cdots, I-1$;

7) $U / R_{B^k} \subseteq U / R_{B^{k+1}}$, 其中$k=1, 2, \cdots, I-1$.

定义9    $ X \subseteq U, X$关于$R_{B^k}$的下近似集和上近似集定义为：

集合$B N_{B^k}(X)=\overline{R_{B^k}}(X)-\underline{R_{B^k}}(X)$称为X的$R_{B^k}$边界域.

由定理3和上述上、下近似的定义易得到如下定理：

定理4   $\left(U, \left\{A^k \mid k=1, 2, \cdots, I\right\}\right)$是一个混合语义下的不完备多尺度信息系统，对于数据填补后的$ S^*, k=1,2, \cdots I, B \subseteq A$，有如下性质成立：$\forall X \subseteq U, Y \subseteq U $.

1) $\underline{R_{B^k}}(X)=\sim \overline{R_{B^k}}(\sim X)$;

2) $\overline{R_{B^k}}(X)=\sim \underline{R_{B^k}}(\sim X)$;

3) $R_{B^k}(\varnothing)=\overline{R_{B^k}}(\mathit{\emptyset})=\varnothing$;

4) $R_{B^k}(U)=\overline{R_{B^k}}(U)=U$;

5) $R_{B^k}(X \cap Y)=R_{B^k}(X) \cap R_{B^k}(Y)$;

6) ${\overline{R_{B^k}}}(X \cup Y)={\overline{R_{B^k}}}(X) \cup {\overline{R_{B^k}}}(Y)$;

7) $X \subseteq Y \Rightarrow \underline{R_{B^k}}(X) \subseteq \underline{R_{B^k}}(Y)$;

8) $X \subseteq Y \Rightarrow \overline{R_{B^k}}(X) \subseteq \overline{R_{B^k}}(Y)$;

9) $R_{B^k}(X \cup Y) \supseteq R_{B^k}(X) \cup R_{B^k}(Y)$;

10) ${\overline{R_{B^k}}}(X \cap Y) \subseteq \overline{R_{B^k}}(X) \cap \overline{R_{B^k}}(Y)$;

11) $R_{B^k}(X) \subseteq X \subseteq \overline{R_{B^k}}(X)$;

12) $\overline{R_{B^{k+1}}}(X) \subseteq R_{B^k}(X), k=1, 2, \cdots, I-1$;

13) $\overline{R_{B^k}}(X) \subseteq \overline{R_{B^{k+1}}}(X), k=1, 2, \cdots, I-1$.

X关于$R_{B^k}$的粗糙度定义为：

可得到不同的尺度下X的近似精度与粗糙度的关系.

定理5    $\left(U, \left\{A^k \mid k=1, 2, \cdots, I\right\}\right)$是一个混合语义下的不完备多尺度信息系统，对于数据填补后的$S^*, k=1, 2, \cdots, I-1, B \subseteq A$，则$\forall X \subseteq U$.

1) $\alpha_{B^{k+1}}(X) \leqslant \alpha_{R_{B^k}}(X)$;

2) $\rho_{B^k}(X) \leqslant \rho_{R^{k+1}}(X)$.

定理5表明，尺度越小(细)，集合X的近似精度越高而粗糙度越小.

在第2节的工作基础之上，本节将给出混合语义下不完备多尺度信息系统的序贯三支决策模型，并基于此模型在混合语义下的不完备多尺度决策系统中选择不确定性最小的尺度作为最优尺度.

定义10    $S=(U, A)=\left(U, \left\{a_j^k \mid k=1, 2, \cdots I, j=1, 2, \cdots, m\right\}\right)$是一个混合语义下的不完备多尺度信息系统，记$A^k=\left\{a_1^k, a_2^k, \cdots, a_m^k\right\}$. 对于数据填补后的$S^*, X \subseteq U$关于$A^k$的三支决策(接受、拒绝和不确定)分别定义为$A C P\left(A^k, X\right), R E J\left(A^k, X\right)$和$U N C\left(A^k, X\right)$. 其中$A C P\left(A^k, X\right)$表示U中在特征关系$R_{A^k}$下一定属于X的对象集，$R E J\left(A^k, X\right)$表示U中在特征关系$R_{A^k}$下一定不属于X的对象集，$U N C\left(A^k, X\right)$表示U中在特征关系$R_{A^k}$下不确定是否属于X的对象集.

定理6    设$S=(U, A)=\left(U, \left\{a_j^k \mid k=1, 2, \cdots I, j=1, 2, \cdots, m\right\}\right)$是一个混合语义下的不完备多尺度信息系统. 对于数据填补后的S^*，k=1，2，…，I-1，根据X关于$ A ^ k $的三支决策，可得到X关于$ A ^{ k +1}$的三支决策.

1) 接受：$A C P\left(A^{k+1}, X\right)=\left\{x \in A C P\left(A^k, X\right) \mid K_{A^{k+1}}(x) \subseteq X\right\} $;

2) 拒绝：$ R E J\left(A^{k+1}, X\right)=\left\{x \in R E J\left(A^k, X\right) \mid K_{A^{k+1}}(x) \cap X=\mathit{\emptyset}\right\}$;

3) 不确定：

证    由定理3知$K_{B^k}(x) \subseteq K_{B^{k+1}}(x)$：

1) 对于$\forall x \in A C P\left(A^k, X\right)$, 始终满足$K_{A^k}(x) \subseteq X$, 于是有$K_{A^{k+1}}(x) \cap X \neq \mathit{\emptyset}$. 因此$x \notin$ $R E J\left(A^{k+1}, X\right)$; 若$K_{A^{k+1}}(x) \subseteq X$则有$x \in A C P\left(A^{k+1}, X\right)$.

2) 对于$\forall x \in R E J\left(A^k, X\right)$, 始终满足$K_{A^k}(x) \cap X=\mathit{\emptyset}$, 于是有$K_{A^{k+1}}(x) \nsubseteq X$. 因此$\notin$ $A C P\left(A^{k+1}, X\right)$; 若$K_{A^{k+1}}(x) \cap X=\mathit{\emptyset}$则有$x \in R E J\left(A^{k+1}, X\right)$.

3) 对于$\forall x \in U N C\left(A^k, X\right)$, 始终满足$K_{A^k}(x) \nsubseteq X$并且$K_{A^k}(x) \cap X \neq \mathit{\emptyset}$, 于是有$K_{A^{k+1}}(x) \nsubseteq$ $X$且$K_{A^{k+1}}(x) \cap X \neq \mathit{\emptyset}$. 因此$x \notin A C P\left(A^{k+1}, X\right)$且$x \notin R E J\left(A^{k+1}, X\right)$.

由以上得到1)2)的证明;

对于$\forall x \in A C P\left(A^k, X\right)$始终有$K_{A^k}(x) \subseteq X$, 因此$K_{A^{k+1}}(x) \cap X \neq \mathit{\emptyset}$, 若$K_{A^{k+1}}(x) \nsubseteq X$则有$x \in U N C\left(A^{k+1}, X\right)$; 对于$\forall x \in R E J\left(A^k, X\right)$始终有$K_{A^k}(x) \cap X=\mathit{\emptyset}$, 因此$K_{A^{k+1}}(x) \nsubseteq X$, 若$K_{A^{k+1}}(x) \cap X \neq \mathit{\emptyset}$则有$x \in U N C\left(A^{k+1}, X\right)$; 对于$\forall x \in U N C\left(A^k, X\right)$始终有$K_{A^k}(x) \nsubseteq X$并且$K_{A^k}(x) \cap X \neq \mathit{\emptyset}$, 因此$K_{A^{k+1}}(x) \nsubseteq X$并且$K_{A^{k+1}}(x) \cap X \neq \mathit{\emptyset}$, 即$x \in U N C\left(A^{k+1}, X\right)$. 由此得到3) 的证明.

由定理6知三支决策$A C P\left(A^k, X\right)$，$R E J\left(A^k, X\right)$和$U N C\left(A^k, X\right)$从k尺度到k+1尺度是单调变化的，变化过程如定理7所示.

定理7    设$S=(U, A)=\left(U, \left\{a_j^k \mid k=1, 2, \cdots I, j=1, 2, \cdots, m\right\}\right)$是一个混合语义下的不完备多尺度信息系统. 对于数据填补后的$S^*, k=1, 2, \cdots, I-1$，有：

1) $A C P\left(A^k, X\right) \supseteq A C P\left(A^{k+1}, X\right)$;

2) $R E J\left(A^k, X\right) \supseteq R E J\left(A^{k+1}, X\right)$;

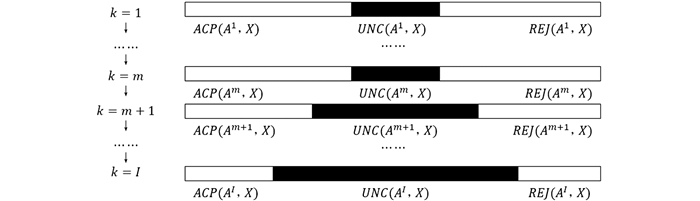
3) $U N C\left(A^k, X\right) \subseteq U N C\left(A^{k+1}, X\right)$.

混合语义下的不完备多尺度信息系统的序贯三支决策模型是在尺度增加(粗化)的过程中对$A C P\left(A^k, X\right)$和$R E J\left(A^k, X\right)$的进一步决策，使得属于$A C P\left(A^k, X\right)$或$R E J\left(A^k, X\right)$的对象可能会增加到$U N C\left(A^{k+1}, X\right)$中. 三支决策从最细尺度到最粗尺度的整个动态过程如图 1所示.

在不完备多尺度决策系统中，尺度越细的决策系统的不确定性越小而在尺度越粗的决策系统中获取的规则越简单^[30]. 本节将利用序贯三支决策的不确定(UNC)量化决策系统的不确定性，选择不确定性最小且尽可能粗的尺度作为最优尺度.

定义11   一个混合语义下的不完备多尺度决策系统可以表示为：

其中$(U, A)=\left(U, \left\{a_j^k \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)$是一个混合语义下的不完备多尺度信息系统. $A$为条件属性集, $d \notin A$为一个单尺度属性, 称为决策属性, $d: U \rightarrow V_d, V_d$为决策属性$d$的值域.

定义12    d(x)为x在决策属性d下的属性值，关于决策属性d的等价关系定义为：

包含x的决策类$[x]_{R_d}=\left\{y \in U \mid(x, y) \in R_d\right\}$. 由决策属性d导出的划分$U / R_d=\left\{[x]_{R_d} \mid x \in U\right\}$.

定理8    设$S=\left(U, \left\{a_j^k \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\} \cup\{d\}\right)$是一个混合语义下的不完备多尺度决策系统，记$A^k=\left\{a_1^k, a_2^k, \cdots, a_m^k\right\}$，对于数据填补后的$S^*, U / R_d=\left\{D_1, D_2, \cdots, D_p\right\}, k=1, 2, \cdots$, $I-1$，根据$D_i \in U / R_d$关于$A^k$的三支决策，可得到$D_i$关于$A^{k+1}$的三支决策.

1) 接受: $A C P\left(A^{k+1}, D_i\right)=\left\{x \in A C P\left(A^k, D_i\right) \mid K_{A^{k+1}}(x) \subseteq D_i\right\}$;

2) 拒绝: $ {REJ}\left(A^{k+1}, D_i\right)=\left\{x \in R E J\left(A^k, D_i\right) \mid K_{A^{k+1}}(x) \cap D_i=\mathit{\emptyset}\right\}$;

3) 不确定：

显然，随着尺度增加，$U N C\left(A^k, D_i\right)$单调不减. 定理6与定理8的不同之处在于三支决策的目标对象不同. 具体来说，前者利用不同尺度下特征关系导出的覆盖对目标概念进行序贯三支决策，而后者则是决策属性导出的划分U/R_d的序贯三支决策.

定义13    $ S=(U, A \cup\{d\})=\left(U, \left\{a_j^k \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\} \cup\{d\}\right)$是一个混合语义下的不完备多尺度决策系统，记$A^k=\left\{a_1^k, a_2^k, \cdots, a_m^k\right\}$，对于数据填补后的$S^*, x \in U$，记：

$\partial_{A^k}(x)$是x关于属性集A在第k尺度下的广义决策值.

定理9    设$S=\left(U, \left\{a_j^k \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\} \cup\{d\}\right)$是一个混合语义下的不完备多尺度决策系统. 对于数据填补后的$S^*, U / R_d=\left\{D_1, D_2, \cdots, D_p\right\} . \forall D_i \in U / R_d$，若$x \in U N C\left(A^k, D_i\right)$，则有$\left|\partial_{A^k}(x)\right|>1$.

证    $\forall x \in U N C\left(A^k, D_i\right)$始终满足$K_{A^k}(x) \nsubseteq D_i$并且$K_{A^k}(x) \cap D_i \neq \mathit{\emptyset}$，于是存在$x_1, x_2 \in$ $K_{A^k}(x)$和$x_3 \in D_i$满足$d\left(x_3\right)=d\left(x_1\right)$而$d\left(x_3\right) \neq d\left(x_1\right)$, 因此$d\left(x_2\right) \neq d\left(x_1\right)$, 也就是$\left|\partial_{A^k}(x)\right|=$ $\left|\left\{d(y) \mid y \in K_{A^k}(x)\right\}\right|>1$.

定义14    设$S=\left(U, \left\{a_j^k \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\} \cup\{d\}\right)$是一个混合语义下的不完备多尺度决策系统. 对于数据填补后的S^*，记$A^k=\left\{a_1^k, a_2^k, \cdots, a_m^k\right\}, U / R_d=\left\{D_1, D_2, \cdots, D_p\right\}$. 若$\exists $$D_i \in U / R_d$使得$U N C\left(A^k, D_i\right)$UNC($A^{k+1}$，$D_i$)并且∀$D_i \in U / R_d$，∀l＜k满足$U N C\left(A^k, D_i\right)=$ $U N C\left(A^l, D_i\right)$，那么就称k为基于不确定性的最优尺度.

由定理7可以得到随着尺度的增加(粗化)$U N C\left(A^k, D_i\right)$单调不减. 通过定义14知，当k为最优尺度时，存在$D_i \in U / R_d$使得$U N C\left(A^k, D_i\right)$随着尺度增加而增大. 因此，最优尺度是使得$U N C\left(A^k, D_i\right)$最小的所有尺度中最粗的尺度. 从不确定性最小即为最优的角度来说，在最优尺度进行决策是有效的.

在尺度细化的过程中，文献[29]选择不确定性不再改变的尺度作为最优尺度. 然而，当增加的尺度是冗余的时，不确定性很容易保持不变^[20]，此时选择的最优尺度的不确定性不是最小. 定义14给出的最优尺度选择方法弥补了此缺陷，得到的最优尺度的不确定性总是最小. 对于一个混合语义下的不完备多尺度决策系统，最优尺度选择步骤如算法1所示.

算法1    混合语义下的不完备多尺度决策系统最优尺度选择

输入：数据填补后混合语义下的不完备多尺度决策系统S^*=(U，A∪{d})=(U，{a_j^k|k=1，2，…，I，j=1，2，…，m}∪{d});

输出：最优尺度k.

1) 计算决策属性的划分：U/R_d={D₁，D₂，…，D_p};

2) for each i∈{1，2，…，p}

3)   计算$A C P\left(A^1, D_i\right), R E J\left(A^1, D_i\right), U N C\left(A^1, D_i\right)$;

4) end for

5) $k=1$;

6) while $k \leqslant I-1$

7)   $end\_condition =0$;

8)   for each $i \in\{1, 2, \cdots, p\}$

9)     initialize $M=\varnothing$;

10)     for each $x \in A C P\left(A^k, D_i\right) \cup R E J\left(A^k, D_i\right)$

11)       if $K_{A^{k+1}}(x) \nsubseteq D_i$ and $K_{A^{k+1}}(x) \cap D_i \neq \mathit{\emptyset}$ then

12)         $M \leftarrow M \cup\{x\}$;

13)     end for

14)     if $M \neq \varnothing$ then

15)       $U N C\left(A^{k+1}, D_i\right)=U N C\left(A^k, D_i\right) \cup M$;

16)       $end\_condition =1$;

17)       break;

18)     else

19)       $U N C\left(A^{k+1}, D_i\right)=U N C\left(A^k, D_i\right)$;

20)     end for

21)     if $end\_condition =1$ then

22)       break;

23)     $k=k+1$;

24) end while

25) return $k$.

算法1首先计算了由决策属性d导出的划分U/R_d，时间复杂度为O(n²). 2-4在第1尺度下计算所有决策类的三支决策，时间复杂度是O(n|p|)，其中每次计算涉及特征集的计算，而每个特征集的计算需要时间复杂度为O(nmI)，所以时间复杂度为O(n²mI|p|). 接着根据序贯三支决策(UNC)计算基于不确定性的最优尺度，有3层循环嵌套，同样内循环涉及特征集的计算，所以在最坏的情况下时间复杂度为O(n²I²m|p|). 所以总的时间复杂度为O(n²I²m|p|).

例3    表 3是一个完成数据补充后的不完备多尺度决策系统S^*=(U，A={a_j^k|k=1，2，…，5，j=1，2，3}∪{d})，其中U={x₁，x₂，…，x₁₀}，关于决策属性的论域划分U/R_d={D₁，D₂}，D₁={x₁，x₂，x₃，x₆，x₇}，D₂={x₄，x₅，x₈，x₉，x₁₀}.

根据算法1，从S^*中选择最优尺度的过程如下：

1) 在第1尺度下, 关于$A^1=\left\{a_1^1, a_2^1, a_3^1\right\}$有$K_{A^1}\left(x_1\right)=\left\{x_1\right\}, K_{A^1}\left(x_2\right)=\left\{x_2\right\}, K_{A^1}\left(x_3\right)=\left\{x_3\right\}$, $K_{A^1}\left(x_4\right)=\left\{x_4, x_6\right\}, K_{A^1}\left(x_5\right)=\left\{x_5\right\}, K_{A^1}\left(x_6\right)=\left\{x_4, x_6\right\}, K_{A^1}\left(x_7\right)=\left\{x_7\right\}, K_{A^1}\left(x_8\right)=\left\{x_8\right\}$, $K_{A^1}\left(x_9\right)=\left\{x_9\right\}, K_{A^1}\left(x_{10}\right)=\left\{x_{10}\right\}$. 显然, $U N C\left(A^1, D_1\right)=\overline{R_{A^1}}\left(D_1\right)-\underline{R_{A^1}}\left(D_1\right)=\left\{x_4, x_6\right\}, U N C\left(A^1\right.$, $\left.D_2\right)=\left\{x_4, x_6\right\}$;

2) 在第2尺度下, 关于$A^2=\left\{a_1^2, a_2^2, a_3^2\right\}$有$K_{A^2}\left(x_1\right)=\left\{x_1\right\}, K_{A^2}\left(x_2\right)=\left\{x_2\right\}, K_{A^2}\left(x_3\right)=\left\{x_3\right\}$, $K_{A^2}\left(x_5\right)=\left\{x_5\right\}, K_{A^2}\left(x_7\right)=\left\{x_7\right\}, K_{A^2}\left(x_8\right)=\left\{x_8\right\}, K_{A^2}\left(x_9\right)=\left\{x_9, x_{10}\right\}, K_{A^2}\left(x_{10}\right)=\left\{x_9, x_{10}\right\}$. 由定理8可得到$U N C\left(A^2, D_1\right)=U N C\left(A^1, D_1\right) \cup \mathit{\emptyset}=\left\{x_4, x_6\right\}, U N C\left(A^2, D_2\right)=\left\{x_4, x_6\right\}$;

3) 在第3尺度下, 关于$A^3=\left\{a_1^3, a_2^3, a_3^3\right\}$, 同理可得$U N C\left(A^3, D_1\right)=U N C\left(A^3, D_2\right)=\left\{x_4, x_6\right\}$;

4) 在第4尺度下, 关于$A^4=\left\{a_1^4, a_2^4, a_3^4\right\}$, 有$U N C\left(A^4, D_1\right)=U N C\left(A^4, D_2\right)=\left\{x_4, x_5, x_6, x_7\right\}$. 因此有$U N C\left(A^3, D_i\right)=U N C\left(A^2, D_i\right)=U N C\left(A^1, D_i\right)(i=1, 2)$而$U N C\left(A^3, D_i\right) \subset U N C\left(A^4\right.$, $\left.D_i\right)(i=1, 2)$. 最后选择第3尺度作为$S^*$的最优尺度.

为了验证在混合语义下的不完备多尺度决策系统中的数据填补和模型扩展以及最优尺度选择算法的可行性与有效性，本研究从UCI数据库中选出5个数据集进行数值模拟，分别为Seeds，Glass Identification，Wholesale Customers，Balance Scale，Car Evaluation，数据集的详细信息如表 4所示.

为满足实验要求，本研究借鉴文献[29]的方法将表 4中的数据集重新构造为多尺度决策系统. 表 5列出了经过预处理后的数据集信息. 在多尺度决策系统中随机丢失一定百分比的条件属性值，从而得到不同缺失率的不完备多尺度决策系统. 若属性值的缺失使得所在属性的值域减小时，将该未知属性值解释为缺席型，否则解释为遗漏型. 最后得到混合语义下的不完备多尺度决策系统.

为验证2.2和2.3小节中的数据填补和模型扩展的有效性，将文献[34]定义的广义不可分辨关系的分类精度μ_R作为评价标准. 具体公式定义为：

其中，在完备信息系统S₁=(U，A)中，E为U上的等价关系，[x]_E表示x的等价类; 在S₁中引入一定百分比的缺失值后有不完备信息系统S₂=(U′，A)，R为U′上广义不可分辨关系(特征关系)，R(x)表示x的广义不可分辨对象集(特征集). 当不完备信息系统S₂导出的覆盖U′/R越接近完备信息系统S₁导出的划分U/E，S₂的分类精度越高; 当S₂导出的覆盖完全还原S₁的划分，则取最大值1.

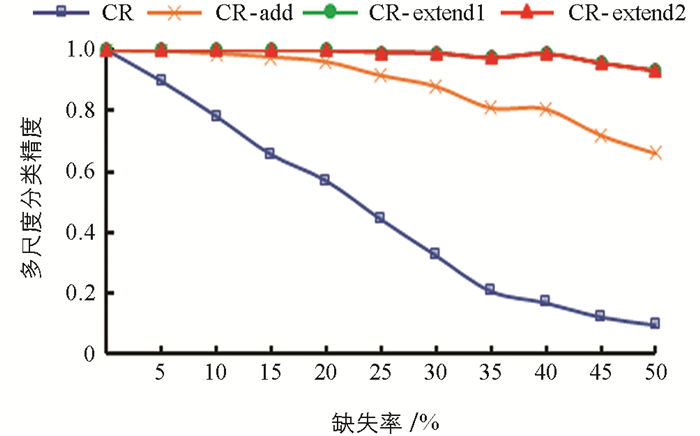
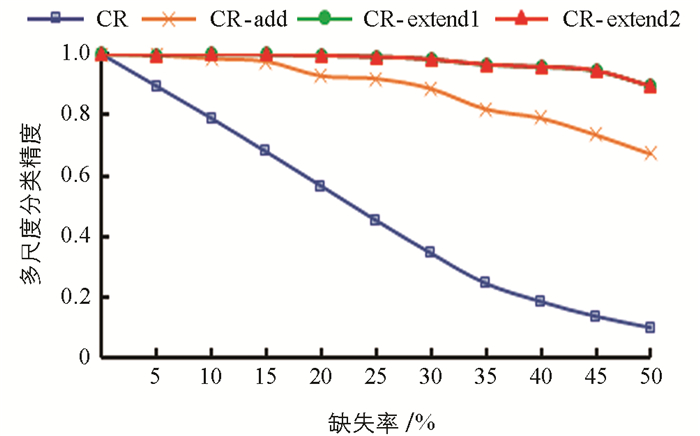
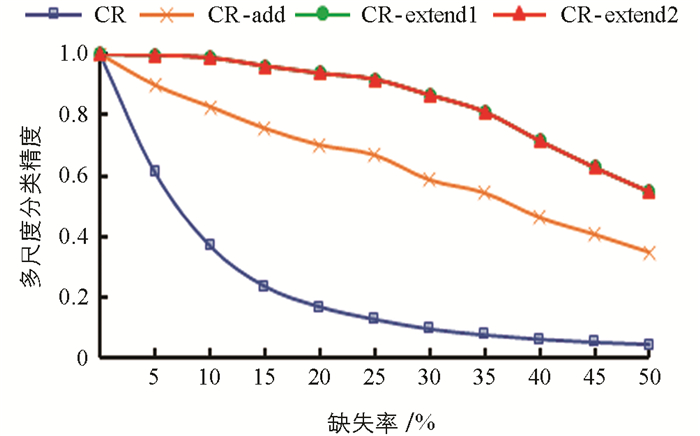
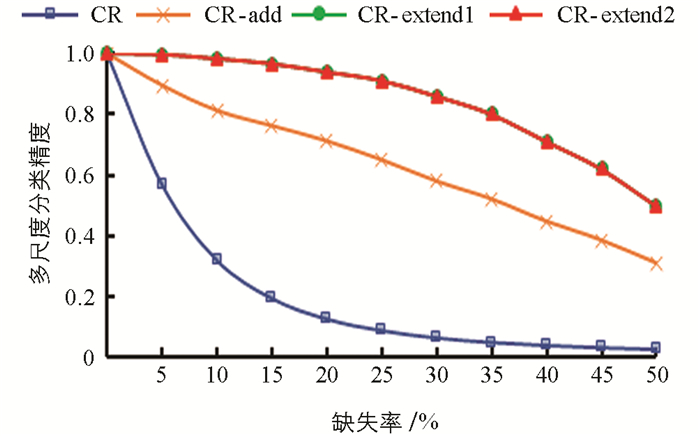
表 6~表 10分别是5个数据集在35%缺失率下4种阶段的单尺度分类精度，图 2~图 6为5个数据集在0~50%的缺失率下4种阶段的多尺度分类精度，多尺度分类精度即为所有单尺度分类精度的平均值. 其中，CR表示将特征关系直接引入不完备多尺度决策系统; CR-add表示在引入特征关系的基础上对系统进行数据填补; CR-extend1指在CR-add的基础上针对特征关系不满足偏序关系的第一次模型扩展，即通过粗尺度下已知属性值的不相等预判细尺度下存在未知属性值的两个对象是不相等的; CR-extend2则是在CR-extend1的基础上针对缺席型未知属性值“$ \mathit{\emptyset} $”的不可比较导致不满足偏序关系而进行的第二次模型扩展.

具体地，针对Seeds数据集，实验结果如表 6和图 2所示. 表 6中第1尺度下数据得不到填补，因此CR-add的分类精度等于CR的分类精度，其余尺度下的分类精度CR-add大于CR; 在第6尺度下，CR-extend1与CR-add的分类精度相同，其余尺度下CR-extend1大于等于CR-add的分类精度; CR-extend2与CR-extend1的分类精度保持不变，对于Glass Identification数据集，CR-extend2相对于CR-extend1的分类精度在尺度1下增高0.005，总体而言变化不大. 针对图 2中的多尺度分类精度，在0~50%的缺失率下，CR-add，CR-extend1相对于前一阶段都得到了或多或少的提升，CR-extend2和CR-extend1持平，即因缺席型未知属性值“$ \mathit{\emptyset} $”的不可比较，未保持偏序关系的模型扩展对分类精度影响不大. 表 7~表 10以及图 3~图 6分别是其他4个数据集的分类精度结果，同样符合Seeds数据集的分析结论. 因此进行数据填补和模型扩展后(CR-extend2)的分类精度相对于直接引入特征关系(CR)的分类精度更高，有利于后续知识获取达到更高的确定性，验证了其有效性.

表 11是5个数据集在5%的缺失率下，经数据填补和模型扩展后算法1的最优尺度实验结果. 其中OLS是算法1得到的基于不确定性的最优尺度. HC'OLS表示文献[29]中定义的最优尺度，其标准是随着尺度变细，不确定性不变的尺度即为最优尺度. 从实验结果可以看出，随着尺度级数的变小(细化)，不确定性存在保持不变后减小的情况. 对于Seeds，Balance Scale和Car Evaluation数据集，HC'OLS的不确定性不是最小的，而本研究提出的方法可得到不确定性最小的最优尺度.

本研究分析发现目前研究中对不完备多尺度信息系统的定义存在局限，因此定义混合语义下的不完备多尺度信息系统，即未知属性值可以是任意的语义解释(遗漏和缺席型未知属性值)并且对象在多尺度属性下缺失时不局限于全部缺失. 引入特征关系以处理此类更为一般的不完备多尺度信息系统，为保持尺度间偏序关系对混合语义下的不完备多尺度信息系统进行数据填补和特征关系的模型扩展，同时给出在不同尺度下信息粒度的表示及其相互关系，定义了集合的上、下近似集概念，并讨论了它们的性质. 基于上述工作，在混合语义下的不完备多尺度决策系统中建立序贯三支决策模型，基于该模型选择不确定性最小的尺度作为最优尺度. 本研究所定义的最优尺度与已有的方法略有不同，选择不确定性最小的尺度作为最优尺度是直观且容易理解的，并且无需从一致和不一致的不完备多尺度决策系统两个角度分别讨论最优尺度. 通过实验证明，经数据填补和模型扩展后，不完备多尺度决策系统的分类精度得到提升，并且选择的最优尺度是所有尺度中不确定性最小的.