Pseudo-spectrum Localization Sets of Tensors

张量的特征值和特征向量是矩阵的特征值和特征向量的推广，在自动控制、数据统计、优化、图像处理、固体力学、量子纠缠和高维马尔科夫链中都有重要的应用^[1-9].复数域上的m阶n维的张量定义为

矩阵伪谱是分析矩阵特征值扰动的重要工具，在控制理论、微分方程数值解等领域都有着举足轻重的应用^[10-11].张量伪谱可以看成是矩阵伪谱的推广，它与齐次动力系统的稳定解息息相关^[12].

令z^m－1=λ，若Re(z) < 0，则齐次动力系统

存在渐近稳定解.为了进一步判断其动力系统是否存在渐近稳定解，利用张量伪谱的定义，文献[12]得到了张量伪谱的圆盘定理，张量伪谱圆盘定理中得到的区域包含所有张量伪谱中的特征值，并且经常被用来判断齐次动力系统渐近稳定解的存在性.

本文通过对张量伪谱的进一步研究，得到了包含张量伪谱的更小的新包含域，新包含域包含所有张量伪谱中的特征值.数值例子验证了结果的有效性.

令$ {r_i}(\mathit{\boldsymbol{A}})= \sum\limits_{\left( {{i_2}, \cdots , {i_m}} \right) \ne (i, \ldots , i)} {\left| {{a_{i{i_2}}} \cdots {i_m}} \right|} , r_i^j(\mathit{\boldsymbol{A}})= \sum\limits_{\left( {{i_2}, \cdots , {i_m}} \right) \ne (i, \cdots , i)} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} - \left| {{a_{ij \cdots j}}} \right|$，可得如下张量伪谱的新包含域：

定理1   设A=(a_i1…im)，E=(e_i1…im)∈C^[m，n]，ε≥0.则

其中

证  令λ∈Λ_ε(A)，设非零向量x∈$\mathbb{C} $ⁿ是特征值λ对应的特征向量，即

令|x_p|=max{|x_i|：i∈N}，则|x_p|≠0，其中N={1，2，…，n}.

若向量x中只有x_p≠0，由(3)式可得

在等式(4)两边同时取绝对值，有

由Hölder不等式，有

由(5)式可得

即λ∈Λ_ε(A)⊆Δ₁(A)⊆Δ(A).

若向量x中至少有两个元x_p≠0，x_q≠0(p≠q)，则有

求解x_p^m－1，有

在等式(6)两边同时取绝对值，有

即

即λ∈Λ_ε(A)⊆Δ₂(A)⊆Δ(A).

定理2   设A=(a_i1…im)，E=(e_i1…im)∈C^[m，n]，ε≥0，则Δ(A)⊆D(A).

证  情形1   若λ∈Λ_ε(A)⊆Δ₁(A)，由定理1可得

即λ∈D(A).

情形2   若λ∈Λ_ε(A)⊆Δ₁(A)，由定理1知，存在p≠q，使得

又因为

则

即

若$\left|a_{{p q} \cdots {q}}\right|\left(r_{p}(\boldsymbol{A})+n^{\frac{m-1}{2}} \varepsilon\right)=0 $，则有

即有λ∈D(A).若$ \left|a_{p q \cdots q}\right|\left(r_{p}(\boldsymbol{A})+n^{\frac{m-1}{2}} \varepsilon\right)>0$，则有

即

或者

也就是说，λ∈D_p(A)或者λ∈D_q(A).即λ∈D(A).

注1  由定理2的结论可知，定理1得到的张量伪谱新包含域比文献[12]中定理3.1的包含域好，但是表达式更复杂，计算量更大.

我们用数值例子来说明结果的有效性.

设A=(a_ijkl)∈C^{[4, 2]}，其中

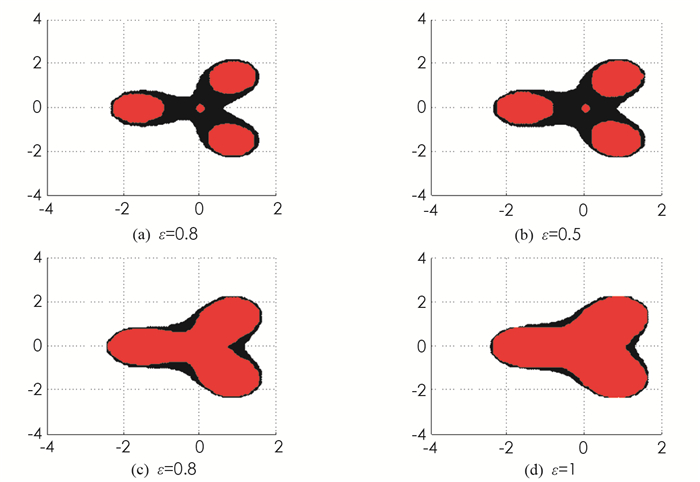
其余的a_ijkl=0.令z^m－1=λ，ε=0.4，0.5，0.8，1，在图 1中，我们给出关于z的包含区域，文献[12]的定理3.1中张量伪谱区域D(A)用黑色表示，定理1中张量伪谱区域Δ(A)用红色表示.由图 1可以看出，定理1的结果比文献[12]中定理3.1的结果好.