-
石墨烯是构建其他维数碳材料如零维富勒烯、一维碳纳米管和三维石墨的基本单元[1],它具有高表面积比、高杨氏弹性模量和导热导电性好等很多非常优异的物理特性,因而在自旋电子学、催化剂、生化传感器、大容量电容器和DNA测序等很多领域中的应用前景十分广阔[2-4].但是,石墨烯的零带隙和较小的开关比[5],不利于大规模集成电路的制作,从而限制了石墨烯在电子器件中的应用.因此,探寻与石墨烯结构相似,既能发挥石墨烯优点又能克服其缺点的类石墨烯等其他二维层状材料,就成为当前材料研究的热点之一.例如,金属硫族化合物材料(TMDs)[6-7]、过渡金属氧化物[5]和其他二维化合物已成为近年来人们高度关注的材料.
氮化铝(AlN)是一种重要的半导体材料,它的高电导率、低介电常数与易匹配的热膨胀系数等优异性能使它成为一种极具吸引力的微电子封装材料[8]. 2016年,Turan S等[9]通过压力烧结方法成功制备了AlN陶瓷材料,该材料可作为优质的储能材料.由于它的非零隙特征使得人们对类石墨烯结构的AlN极为重视.文献[10-12]基于密度泛函理论计算了Ⅳ-Ⅳ和Ⅲ-Ⅴ结构ANB8-N类石墨烯化合物,结果表明这些类石墨烯化合物具有稳定的能量和结构. Ganji M D等[13]利用vdW-DF法研究了以石墨烯为基底的AlN的DMMP吸附,Camacho-Mojica D C等[14]通过密度泛函方法研究了AlN薄膜的线缺陷.在实验方面,已成功制备了各种AlN纳米级薄膜或者切片,以及石墨烯与类石墨烯薄膜组成的复合薄膜,并对相应热导率等性能进行了系统研究[15-17].另外,文献[18-19]利用哈里森键联轨道法研究了二维化合物ANB8-N类石墨烯的弹性和介电性质以及π键和σ键的极性、键能、内聚能和有效原子电荷等.但是,这些研究未考虑到原子振动的非简谐效应,因而不能反映这些物理量随温度的变化规律,而且未对AlN类石墨烯材料的热膨胀系数、弹性模量等极为重要的热力学量进行研究.实际上,非简谐振动无论对三维、二维甚至一维材料的热力学性都有极为重要的影响,因此近年来非简谐效应的研究已成为新材料研究的热点之一.例如,明庭尧等[20-21]对石墨烯的非简谐效应及对其热学、电学性能进行了研究;Ribeiro G A S等[22]基于第一性原理方法详细研究了PbTe和SnTe的非简谐效应及其对声子谱的影响. Kringhøj A等[23]从实验上对Josephson隧道结的非简谐效应进行了系统研究.然而,到目前为止,还未发现对AlN类石墨烯材料的热力学性能进行研究.因此,本研究在考虑到原子的非简谐振动基础上,应用固体理论和方法,对AlN类石墨烯材料的热膨胀系数、格林乃森参量和弹性模量等重要热力学量进行深入研究,以期有助于研发具有稳定性能的电子器件.
HTML
-
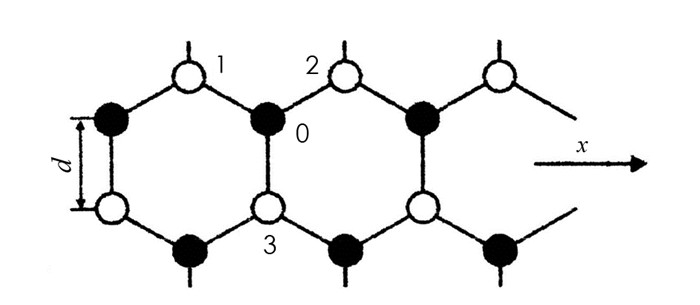
本文主要研究单层AlN类石墨烯材料的热力学性质.单层AlN类石墨烯材料的结构见图 1,图 1中黑色原子(A原子)和白色原子(B原子)构成的二维六角格子平面系统.设A原子数和B原子数均为N,最近邻原子间距离为d(称点阵常数),取任一原子为坐标系原点,x方向向右,y方向竖直向上,z方向垂直纸面向外.
图 1中AlN类石墨烯材料的化学键与石墨烯相似,即面内为3个sp2杂化轨道形成的σ键,每个σ键中填充2个电子,分别由Al和N原子提供,导致每个原子近邻分布3个异族原子;垂直方向上是相邻原子的pz轨道杂化形成π健,该化学键的电子来自N原子提供的孤对电子.原子的相互作用能包括:金属化能、共价能、极化能.其中,σ键的金属化能为V1=
$\sqrt{\frac{1}{2}\left[\left(V_{1}^{\mathrm{A}}\right)^{2}+\left(V_{1}^{\mathrm{B}}\right)^{2}\right]}$ ,式中V1A=$\frac{{1 }}{{3}}$ (εpA-εsA),V1B=$\frac{{1 }}{{3}}$ (εpB-εsB).这里εhA和εhB分别是A和B原子的杂化轨道能,由它们的杂化情况决定.对sp2杂化情况,杂化能εhk=(εs+kεp)/(k+1),这里的εs和εp分别是s和p轨道的能量. σ键的共价能为V2=η2ħ2/md2,d是原子间距离,ħ是普朗克常数,m是自由电子质量.对sp2杂化,η2=3.26[20]. σ键的极化能V3=|εhA-εhB|/2.而π键的共价能为V2=ηppπ(ħ2/md2),ηppπ=0. 63;极化能为V3=|εpA-εpB|/2.为简化,引入极性参量αp和αp*,和共价参量αc和αc*,定义为:
对σ键
对π键
此外,还有短程相互作用能和交换能,其中短程相互作用能ΔErep与键长d的关系为:ΔErep=C(a0/d)12,这里a0是玻尔半径,而C=0.20 eV.交换能为2S(V2+V2*/
$\sqrt{3}$ ),S为交换积分参量.考虑到短程相互作用后,可将相互作用能φ随原子间距离d的变化写为[6]式中:
$ R= \sqrt{V^{2}_{2}+V^{2}_{3} }, R^{·}= \sqrt{V^{·}_{2}+V^{·}_{3}}$ ;第1,2项分别是σ键和π键的贡献;第3项是极化的贡献;第4项是交换能;第5项是短程相互作用的贡献.利用平衡态下能量极小的条件,求出交换积分参量S,最后得到平衡态下一个原子的平均相互作用能为[19]
-
类石墨烯的原子会在沿键长方向作非简谐振动,简谐系数ε0、第1,2阶非简谐振动系数分别为ε1和ε2,它们与原子相互作用能关系为
将(3)式代入(4)式,考虑到π键的贡献很小,由(5)式求得:
-
晶体中的原子各自在平衡位置作非简谐振动,由于原子间相互作用势随原子间的距离而变化,而振动频率ω取决于原子的质量和原子间相互作用势,因而振动频率ω不为常量,而与原子间的距离有关,即与晶体的尺寸如体积V(三维)、面积S(二维)和长度L(一维)有关. ω随尺寸的变化程度反映了非简谐效应的大小,可通过格林乃森参量(γG)来描述. AlN类石墨烯材料为二维晶体,定义
$γ_{\rm G}=- \frac{{∂\ln ω}}{{ ∂\ln S}} $ ,它与温度T和简谐系数ε0、第一、二阶非简谐系数ε1和ε2的关系为[8]:式中:r0为平衡时原子间的距离,kB为玻尔兹曼常数. (9)式表明,简谐近似时,即ε1=0,ε2=0,格林乃森参量为零.非简谐情况下γG与温度有关.温度越高,γG值越大,即非简谐效应越显著.
在非零温时,原子作非简谐振动使最近邻原子间距离由d0变为d(T)=d0+δ(T),其中的原子平均位移δ(T)由统计物理求得[24]
结合线膨胀系数αl=(1/d0)(dδ/dT),可求得
-
考虑到原子非简谐振动后,最近邻原子间距离为
压缩系数KT为弹性模量B的倒数,文献[19]给出石墨烯的弹性模量B与原子间距离和原胞面积Ω=(
$\sqrt{3}$ /2)d02的关系为B=ε0d2/Ω.将(11)式代入(12)式,再代入B,可得到弹性模量随温度的变化为
2.1. AlN类石墨烯材料原子振动的简谐系数和非简谐系数
2.2. AlN类石墨烯材料的格林乃森参量和热膨胀系数随温度的变化
2.3. AlN类石墨烯材料的弹性模量随温度的变化
-
文献[19]给出了AlN类石墨烯的V1、σ键的共价能V2、σ键的极化能V3、π键的共价能V2*、π键的极化能V3*和最近邻原子间距离d0等有关数据(表 1),由此算出的极性参量αp和共价参量αc也列于表 1中.
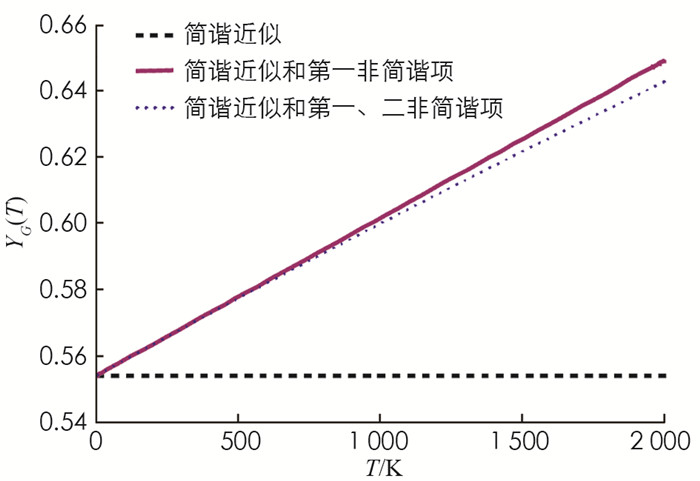
将表 1的数据以及C=0.20 eV,代入(6)、(7)、(8)式,可求得ε0=0.507×102J/m2,ε1=-0.947×1012J/m3,ε2=-0.225×1022J/m4.将表 1的数据和得到的ε0,ε1和ε2代入(9)式,可得到AlN类石墨烯材料的格林乃森参量随温度的变化(图 2),图 2中虚线、点线和实线分别表示只考虑简谐近似,考虑简谐项和第一非简谐项和同时考虑简谐项与第一、二非简谐项的结果.
由图 2看出,简谐近似下,格林乃森参量几乎不变,为0.554;考虑到非简谐项后,格林乃森参量随温度的升高而增大,在0.554~0.650间变化;同时考虑第一、二非简谐项后,温度不太高时,格律乃森参量与只考虑第一非简谐项时相差很小,即第二非简谐项对格林乃森参量的影响很小,几乎可以忽略;但是,当温度较高时(例如高于1 000 K),影响比较明显,且随温度的增加,影响逐步增加;考虑到非简谐项后的格林乃森参量与简谐近似的差ΔγG=γG-γG0随着温度升高而增大,表明温度愈高,非简谐效应愈显著.例如,在T=300 K时,差值约为0.013;而在温度T=1 000 K时,差值约为0.046.
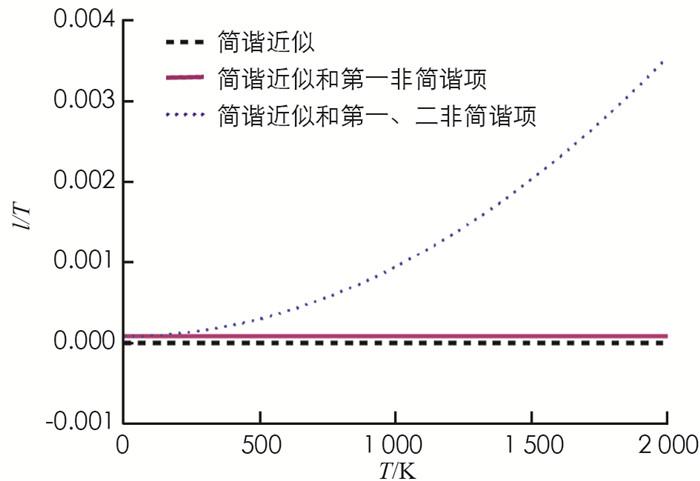
将图 2和ε0,ε1,ε2等数据代入(11)式,可求得AlN类石墨烯材料的线膨胀系数随温度的变化(图 3),图 3中的虚线、实线和点线分别表示只考虑简谐近似,考虑简谐近似和第一非简谐项,同时考虑到简谐近似和第一、二非简谐项的结果.
由图 3看出,在简谐近似下,AlN类石墨烯材料的热膨胀系数为零;若只计及第一非简谐项,则热膨胀系数为常数8.57×10-5 K-1;同时考虑到第一、第二非简谐项,则热膨胀系数随温度升高而非线性增大,变化范围在8.57×10-5~3.6×10-3 K-1之间.这表明,热膨胀系数随温度变化主要由原子振动的第二阶非简谐项造成.相反地,简谐效应和第一非简谐效应的影响几乎为零.非简谐项对热膨胀系数的影响随着温度升高而增大,即温度愈高,非简谐效应愈显著.另外,特别值得注意两点是:①AlN类石墨烯材料虽与石墨烯具有相似的二维平面六角格子结构(图 1),但各格点上的原子不同,导致它们的物理性能存在明显差异.例如:石墨烯热膨胀系数为负值-5. 41×10-6K-1,而AlN类石墨烯材料的线膨胀系数为正. ②热力学性能随维度不同也存在明显差异.例如,T=500 K时,第一性原理计算的六角AlN块体(三维晶体)热膨胀系数约为1.901×10-5K-1[24],明显小于本文中AlN类石墨烯材料(二维晶体)热膨胀系数2.995×10-4K-1.
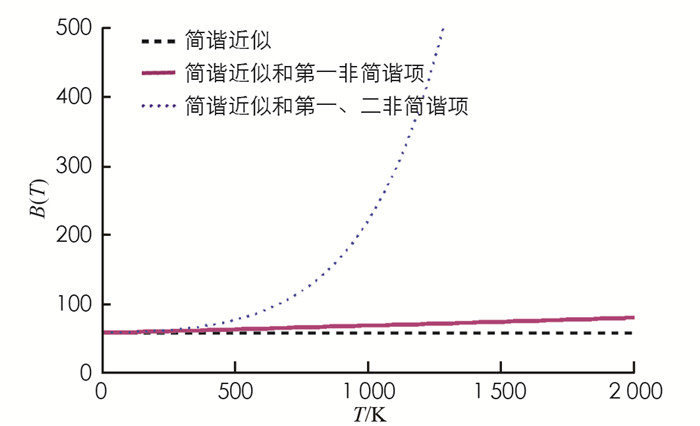
将表 1和ε0,ε1,ε2等数据代入(11)式后可求得线膨胀系数αl,再代入(13)式,可得到AlN类石墨烯材料弹性模量随温度的变化(图 4). 图 4中的虚线、实线和点线分别表示只考虑简谐近似,考虑简谐近似和第一非简谐项,同时考虑简谐近似和第一、二非简谐项的结果.
由图 4看出,在简谐近似下,AlN类石墨烯材料的弹性模量为常量;考虑到非简谐项后,弹性模量随温度的升高而在58.54~500.00 N/m之间非线性增大.其中,当只计及到第一非简谐项时,弹性模量随温度升高线性增大,且变化极小,在0~2 000 K的温度范围内,只增大约0.024%.计及到第一、二非简谐项时,弹性模量随温度升高而迅速增大;考虑到非简谐项时,弹性模量与简谐近似下的差值随着温度升高而增大,即温度愈高,非简谐效应愈显著.考虑到非简谐项后,本研究理论值与文献[25]在考虑到第一非简谐项情况下对石墨烯的计算结果非常接近,例如当T=1 000 K时,本研究的AlN类石墨烯材料B=222 N/m,接近于石墨烯的B=204 N/m.
-
本研究基于量子固体理论,充分考虑了原子振动的非简谐效应,搭建了固体物理模型,对AlN类石墨烯材料的热力学性质随温度的变化进行了深入研究.研究发现,AlN类石墨烯材料的格林乃森参量、线膨胀系数、弹性模量等热力学量均与第一、二阶非简谐系数密切相关.在简谐近似下,AlN类石墨烯材料不发生热膨胀,即线膨胀系数为零;它的格林乃森参量和弹性模量均为常量.这明显与实验不符,因此研究热学性质必须考虑非简谐效应.考虑到原子振动的非简谐效应后,格林乃森参量、线膨胀系数和弹性模量均随温度的升高而非线性增大,相应的变化范围分别为0.547~0.630,8.57×10-5~3.60×10-3K-1和58.54~500.00 N/m,即温度愈高,非简谐效应愈显著. AlN类石墨烯材料的线膨胀系数和弹性模量在数值上虽与AlN块状晶体不同,但它们随温度的变化规律相似.






 DownLoad:
DownLoad: