On Dynamics of an HBV Model with Intermittent Antiviral Therapy

对于间歇性抗病毒治疗方法，考虑到病毒的自由移动，建立如下具有标准发生率的空间依赖HBV模型

具有齐次Neumann边界条件

其中Ω是$\mathbb{R}$ⁿ中的有界域，且具有光滑边界∂Ω.

初值条件为

其中u(x，t)，w(x，t)和v(x，t)分别表示在时刻t处位置为x的正常细胞、感染细胞和自由病毒的浓度.其他参数见表 1.

间歇治疗指的是当HBV-DNA水平上升到一定值时才开始治疗，经过治疗后，该水平下降到可容忍量就停止治疗，所以设置参数m取值如下：

其中：c₀表示停止治疗的HBV-DNA浓度阈值，c₁表示开始治疗的HBV-DNA浓度阈值.

首先给出一些定义.令$\mathscr{X}$：=C(Ω，$\mathbb{R}$³)，其范数为上确界范数‖·‖.定义$\mathscr{X}$⁺：=C(Ω，$\mathbb{R}$₊³)，则($\mathscr{X}$，$\mathscr{X}$⁺)是一个强有序空间.

定理1  对任意初值函数ϕ ∈$\mathscr{X}$⁺，系统(1)-(3)存在唯一定义在[0，+∞)上的解W(·，t，ϕ)，且W(·，t，ϕ)∈$\mathscr{X}$⁺，系统(1)-(3)在$\mathscr{X}$⁺内的所有解都是一致最终有界的.

证  (i)先证明解的存在唯一性和W(·，t，ϕ)∈$\mathscr{X}$⁺.

对任意的ϕ =(ϕ₁，ϕ₂，ϕ₃)^T∈$\mathscr{X}$⁺和x∈ Ω，定义F=(F₁，F₂，F₃)：[0，+∞)×$\mathscr{X}$⁺ $\mathscr{X}$如下：

则对任意初值ϕ =(u⁰(x)，w⁰(x)，v⁰(x))，原系统(1)-(3)可写为如下抽象系统

其中W =(u，w，v)^T，AW =(0，0，dΔv)^T.显然，F在$\mathscr{X}$内满足局部Lipschitz条件，由文献[15]知，系统(5)在[0，T_max)存在唯一的局部解W(·，t，ϕ)，其中T_max表示解的最大存在时间，且当t∈[0，T_max)时，W(·，t，ϕ)∈$\mathscr{X}$⁺.最后，由比较定理、文献[16]中的类似讨论和半线性抛物系统的标准理论知可将T_max延拓到+∞.

(ii) 再证明解的最终有界性.

令U=u+w，则U满足

其中δ=min{μ₁，μ₂}.进而对于x∈ Ω，有$\mathop {{\text{lim}}}\limits_{t \to \infty } {\text{sup}}U(x, t) \leqslant \frac{\lambda }{\delta } = M$，所以存在0 < ε$\ll $1和${\tilde t_0}$>0，使得U(·，t)≤(1+ε)M，∀t≥${\tilde t_0}$，即u和w是一致最终有界的.

由w的有界性可得，

令v是下面常微分方程的解

则有$\mathop {{\text{lim}}}\limits_{t \to \infty } {\text{sup}}\bar v(t) \leqslant \frac{{k(1 + \varepsilon)M}}{{{\mu _3}}} = \bar M$.

由比较定理可得v(x，t)≤ v(t).所以存在$ {{\overset{\wedge }{\mathop{t}}\,}_{0}}$≥${\tilde t_0}$>0和0 < ε $\ll $1，使得

即v是一致最终有界的，证毕.

下面构造解的正不变集.令

结合系统(1)-(3)定义半流Ψ_t：$\mathscr{X}$⁺→$\mathscr{X}$⁺为：

其中W(·，t，ϕ)是系统(1)-(3)具有初值W(·，0，ϕ)= ϕ ∈$\mathscr{X}$⁺的解.因为(1+ε)M和(1+$\bar \varepsilon $)M分别是系统(6)和(7)的上解，结合比较原理可知$\mathscr{D}$对于Ψ_t是正不变的，即有Ψ_t(ϕ)∈$\mathscr{D}$，∀t≥0，ϕ ∈$\mathscr{D}$.

因为系统(1)-(3)中的前两个方程里没有扩散项，所以其解半流Ψ_t是非紧的.下通过引入非紧性Kuratowski测度κ^[17]以解决非紧性问题.对任意有界集B，定义

若B是无界的，则κ(B)=∞.易知当且仅当κ(B)=0时B是预紧的.

令

引理1^[18]  假设存在常数c>0使得

其中f (u，w，v)=(f₁(u，w，v)，f₂(u，w，v)).则Ψ_t是κ收缩的，即对任意有界集B$\subset $$\mathscr{X}$⁺，有

对于引理1中的条件(8)，由于

其中$a = \frac{{(1 - m{e_1}(t))\beta wv}}{{{{\left({u + w} \right)}^2}}}, b = \frac{{(1 - m{e_1}(t))\beta uv}}{{{{\left({u + w} \right)}^2}}}$.而$\left| {a - b} \right| = \left| {\frac{{(1 - m{e_1}(t))\beta v(w - v)}}{{{{\left({u + w} \right)}^2}}}} \right| < \left| {\frac{{(1 - m{\underline e _1})\beta v}}{{u + w}}} \right|$，其中e₁=min{e₁(t)}.又由$\frac{{\partial U}}{{\partial t}} = \lambda - {\mu _1}u - {\mu _2}\; w \geqslant \lambda - {\text{max}}\{ {\mu _1}, {\mu _2}\} U$可知：存在0 < ε$\ll $1和L使得u+w≥(1-ε)L，故有$\left| {a - b} \right| < \left| {\frac{{(1 - m{\underline e _1})\beta \left({1 + \bar \varepsilon } \right)\bar M}}{{(1 - \varepsilon)L}}} \right|$，综上可知当${\mu _i} > \frac{{\left| {a - b} \right|}}{2}\left({i = 1, 2} \right)$时，引理1中的常数c存在.

在治疗前，也即m=0时，由文献[16]知，原系统的基本再生数为

令系统(1)中3个方程的右端为0，求解后可得如下平衡态的存在性结论：

定理2  (i)如果R₀ < 1，则原系统(1)-(3)存在唯一的疾病消除平衡态${E_0}\left({\frac{\lambda }{{{\mu _1}}}, 0, 0} \right)$.

(ii) 如果R₀>1，则原系统(1)-(3)存在一个疾病消除平衡态${E_0}\left({\frac{\lambda }{{{\mu _1}}}, 0, 0} \right)$和一个感染平衡态E^*(u^*，w^*，v^*)，其中

关于平衡态的稳定性有如下结论：

定理3  当R₀ < 1时，E₀是全局渐近稳定的，即对任意初值属于C^γ(Ω，$\mathbb{R}$₃⁺)(0 < γ < 1)，都有

反之，当R₀>1时，E₀不稳定.

在证明定理3之前，先考虑下面二阶抛物方程初边值问题解的一致估计：

其中：L[u]=-a_ij(x)D_iju+b_i(x)D_iu+c(x)u，B[u]=u或$B[u] = \frac{{\partial u}}{{\partial \mathit{\boldsymbol{n}}}} + b(x)u, b \in {C^{1 + \alpha }}(\partial \mathit{\Omega})$且b≥0.当B[u]=u时，有f(x，0，0)=0，x∈∂Ω.

假设a_ij，b_i，c∈C^α(Ω)，φ∈W_p²(Ω)，$p > 1 + \frac{n}{2}$，B[φ]|_∂Ω=0.定义Q_∞=Ω×[0，∞).

关于系统(9)解的一致估计，有：

引理2^[19]  令∂Ω∈C²，u是系统(9)的一个全局解，且对某σ，ω∈$\mathbb{R}$有σ≤u≤ω.假设f∈L^∞(Q_∞×[σ，ω])，则对任意给定的τ>0，存在常数C(τ)使得

定理3的证明  因为u⁰，w⁰∈C^γ(Ω)，所以由u，w和v的方程及引理2可推得存在0 < α，α′ < 1和常数C>0使得

对系统(1)-(3)在E₀处构造如下Lyapunov函数

其中${u_0} = \frac{\lambda }{{{\mu _1}}}, f(x, y, z) = \frac{{\beta x\; z}}{{x + y}}$.显然对任意的t≥0有V(t)≥0.

因为u≤C，ω≤C，所以沿着系统(1)-(3)的解对V关于t求导得

当R₀ < 1时，定义${\psi _1}(t) = \int_\mathit{\Omega} {\left({\frac{{{\mu _1}w}}{{C({u_0} + C)}}{{(u - {u_0})}^2}} \right){\text{d}}x, \psi {i_2}(t) = \int_\mathit{\Omega} {\left({\frac{{{\mu _2}{\mu _3}}}{k}(1 - {R_0})v} \right)} {\text{d}}x} $.由(10)和(11)式可得存在C₁>0使得‖ψ₁‖_{C^α([1，∞))}≤C₁，${\left\| {{\psi _2}} \right\|_{C{^{\frac{{(1 + \alpha \prime)}}{2}}}\left({\left[{1, {\text{ }}\infty } \right)} \right)}} \leqslant {C_1}$.所以由文献[19]中的引理1.1可知当t→∞时有ψ_i(t)→0(i=1，2).所以有

因为‖v(·，t)‖_{C^1+α′(Ω)}≤C，所以存在序列{t_n}和非负函数$\mathop v\limits^ \wedge $ ∈C¹(Ω)使得

从而，由$\underset{t\to \infty }{\mathop{\text{lim}}}\,\ {{\left\| v \right\|}_{{{L}^{1}}(\mathit{\overline{\Omega }})}}=0$可知$\mathop v\limits^ \wedge $ =0，所以

所以对任意的ε>0，存在t₀>1使得当t>t₀时‖v(·，t)‖_C((Ω)) < ε和e^-μ₂t < ε成立.由第二个方程可知，当t>t₀时

因此，当t>t₀时，

所以

由第一个方程可得

通过类似于上面的讨论显然

下证当R₀>1时，E₀是不稳定的.

令0=υ₁ < υ₂ < … < υ_n < …为算子-Δ在具有Neumann边界条件的区域Ω上的特征值.令E(υ_i)为在C¹(Ω)内相应于υ_i的特征函数空间.令{e_ij：j=1，2，…，dim E(υ_i)}是E(υ_i)的标准正交基，$\mathbb{Y}$=[C¹(Ω)]³，$\mathbb{Y}$_ij={ce_ij：c∈$\mathbb{R}$³}.则有

原系统在任意平衡点E_e(u_e，w_e，v_e)的线性化系统为

其中D=diag(0，0，d)且

令LZ=DΔZ+AZ(x，t).对每个i≥1，$\mathbb{Y}$_i在算子L下是不变的，且ξ是L的特征值当且仅当对某i≥1，ξ是特征方程det(-υ_iD+A-ξI)=0的根，此时，在Y_i内有一个特征向量.

易知，对任意的i≥1，原系统在平衡点E₀处的特征方程det(-υ_iD+A-ξI)=0为

令h_i(ξ)=ξ²+(μ₂+μ₃+υ_id)ξ+μ₂υ_id+μ₂μ₃(1-R₀).当i=1时，υ_i=0.此时h₁(ξ)=ξ²+(μ₂+μ₃)ξ+μ₂μ₃(1-R₀).当R₀>1时，h₁(ξ)有一个正根，所以E₀不稳定.证毕.

定理4  当R₀>1时，E^*(u^*，w^*，v^*)是全局渐近稳定的，即对任意初值属于C^γ(Ω，$\mathbb{R}$₃⁺)(0 < γ < 1)，都有

证  对系统(1)-(3)在E^*处构造如下Lyapunov函数

其中$f(x, y, z) = \frac{{\beta x\; z}}{{x + y}}$.通过类似于定理3的证明易得结论成立.

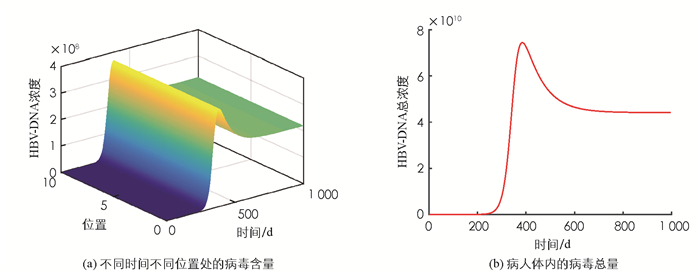
由3.1的分析可知，在未接受治疗前，疾病是否消除由基本再生数决定.事实上，对于大部分乙肝病人来说，其体内的病毒是不会完全消除的，若不接受治疗，在病毒活跃期，病毒会大量复制并达到一个平衡状态. 图 1显示了此种情况，在某组参数取值下，病人体内的病毒在不到3年时间内高速复制并达到稳定.

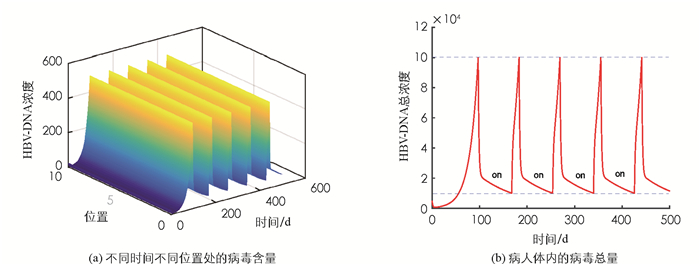
我们通过数值模拟探讨间歇性抗病毒治疗方式的治疗效果.在(4)式中，取c₀=10 000，c₁=100 000，也即如果病毒量维持在10 000单位以下，治疗停止；一旦病毒量上升到100 000单位以上，则开始接收治疗，直到降到可容忍范围内为止.参数取值为：λ=20 000，β=0.000 5，μ₁=0.003 79，μ₂=0.012 81，μ₃=0.67，d=0.17，k=100，${e_1}(t) = {\text{ }}\frac{{0.9}}{{1 + {e^{ - t}}}}, {e_2}(t) = \frac{{0.8}}{{1 + {e^{ - t}}}}$.从图 1，2明显看到，病人体内病毒在3个月左右已上升到临界值，在后面的2个月之内接受间歇性抗病毒治疗效果良好.

我国是乙肝发病大国并呈地方病态势.当前的抗病毒药物只能抑制病毒复制，并不能将其彻底消除，而连续治疗方式会造成抗药性提前、副作用大和花费高等不利影响.为了探索更好的治疗方式，本文基于间歇性抗病毒治疗具有延缓耐药性发展并减小副作用等优点，建立了一个间歇性抗病毒治疗的HBV扩散模型，对其动力学行为进行了理论分析和数值模拟，所得结果为间歇性抗病毒治疗方法提供了理论支持.