On Hopf Bifurcation and Stability for a Charge Transfer Model

本节研究系统(1)对应的ODE系统：

Hopf分支的存在性和稳定性.

当外部电流固定时，求得系统(2)的正平衡点为(a^*，u^*)，其中${{a}^{*}}=~\frac{{{j}_{0}}}{T({{j}_{0}}^{2}+1)}$，u^*=a^*+j₀.经计算，系统(2)在正平衡点(a^*，u^*)处的雅可比矩阵为

其特征方程为

这里$\text{tr}\boldsymbol{J}=\frac{{{j}_{0}}^{2}-1}{{{({{j}_{0}}^{2}+1)}^{2}}}-T-D,\ \text{det}\boldsymbol{J}=DT>0$.

下面以D为参数讨论系统(2)在(a^*，u^*)处的稳定性及Hopf分支.

定理1  设${{D}_{0}}=\frac{~{{j}_{0}}^{2}-1}{{{({{j}_{0}}^{2}+1)}^{2}}}~-T>0$，则有

(i) 当D>D₀时，系统(2)的唯一正平衡点(a^*，u^*)局部渐近稳定；当0 < D < D₀时，系统(2)的唯一正平衡点(a^*，u^*)不稳定；

(ii) 当D=D₀时，系统(2)在(a^*，u^*)处产生Hopf分支，且当1 < j₀² < 3+2 $\sqrt{2}$时，该Hopf分支为次临界方向，周期闭轨渐近稳定；当j₀²>3+2 $\sqrt{2}$时，该Hopf分支为超临界方向且不稳定.

证  (i)当D>D₀时，trJ < 0，detJ>0，系统(2)在(a^*，u^*)处雅可比矩阵J的所有特征值实部均小于0，此时(a^*，u^*)局部渐近稳定；当0 < D < D₀时，trJ>0，detJ>0，系统(2)在(a^*，u^*)处雅可比矩阵J存在正实部的特征值，此时(a^*，u^*)不稳定.

(ii) 设λ=α(D)±iβ(D)为特征方程的两个根，则

经计算得α(D₀)=0，α′(D₀)=-$\frac{1}{2}$≠0，则系统(2)在D=D₀处可能产生Hopf分支.下面通过计算其一阶焦点量给出Hopf分支的存在性及其方向和稳定性.

令$\tilde{a}$=a－a^*，$\tilde{u}$=u－u^*.为方便起见，仍用a和u分别表示和$\tilde{a}$，$\tilde{u}$系统(2)变形为

进而有

其中

做变换

其中

则(3)式可进一步化为

其中

经计算可得G¹(x，y，D)，G²(x，y，D)在(0，0，D₀)处的各阶导数值为

其中

由Hopf分支定理^[9]可知，Hopf分支的方向和稳定性由b(D₀)，α(D₀)，α′(D₀)决定，其中

将各阶导数值代入可得

其中

从而有

因此，由文献[10]知：当1 < j₀² < 3+2 $\sqrt{2}$时，b(D₀) < 0，分支周期解是稳定的，注意到α′(D₀) < 0，则Hopf分支为次临界方向；当j₀²＞3+2 $\sqrt{2}$时，b(D₀)>0，分支周期解不稳定，且该Hopf分支为超临界方向.证毕.

注1  条件α(D₀)=0，α′(D₀)≠0仅为系统(2)产生Hopf分支的必要条件.对于系统

平衡点为(0，0)，其雅可比矩阵的特征值虽然满足α(0)=0，α′(0)≠0，但系统在D=D₀处的一阶焦点量为零，不存在周期解，即不产生Hopf分支.

下面在一维空间讨论带扩散的动力系统

的Hopf分支.

令X_c=X+iX，其中X={(a，u)∈(H²[(0，π)])²：a_x=u_x=0，x=0，π}.系统(4)在(a^*，u^*)处定义在X_c上的线性化算子形式如下：

其中d=diag(D_a，D_u).

令

将(7)式代入L的特征方程

得

其中

令|J_k－μI|=0，则L的特征方程为

这里

设μ=α_k(D)±iβ_k(D)，k=0，1，2……是L(D)的特征值，则有

当k≥1时，设H₀(k²)：=detJ_k(D₀)，若D_a≥D_u，则detJ_k(D₀)>0；若D_a < D_u，则当H₀(k²)判别式为负，即

等价于

时，detJ_k(D₀)>0.解不等式(12)得

代入D₀的表达式，并令${{\overset{\wedge }{\mathop{j}}\, }_{0}}=\frac{\sqrt{{{j}_{0}}^{2}-1}}{{{j}_{0}}^{2}+1}$，则当D_a < D_u时，只要

即有detJ_k(D₀)>0.

综上分析可知，对任意的k≥1，当D_a，D_u满足不等式(14)时，detJ_k(D₀)>0，此时L(D₀)的特征值除一对共轭纯虚根外，其余特征值均具有负实部，故系统(5)在(a^*，u^*，D₀)处产生Hopf分支.

定理2  当D_a，D_u满足条件(14)时，系统(5)在(a^*，u^*，D₀)处产生空间齐次的Hopf分支.当1 < j₀² < 3+2 $\sqrt{2}$时，该Hopf分支的方向次临界且周期闭轨渐近稳定；当j₀²＞3+2 $\sqrt{2}$时，该Hopf分支的方向超临界且不稳定.

证  设L^*是系统(5)在(a^*，u^*，D₀)处线性化算子L的伴随算子

其中

令

满足

其中$\left\langle {{\mathit{\boldsymbol{q}}^*}, \mathit{\boldsymbol{q}}} \right\rangle = \int_0^\pi {{{\overline {{\mathit{\boldsymbol{q}}^*}} }^{\rm{T}}}} \mathit{\boldsymbol{q}}dx, \left\langle {{\mathit{\boldsymbol{q}}^*}, \mathit{\boldsymbol{\overline q}}} \right\rangle = \int_0^\pi {{{\overline {{\mathit{\boldsymbol{q}}^*}} }^{\rm{T}}}} \mathit{\boldsymbol{\overline q}} dx$.

令

则有

作如下定义

其中

根据(17)-(21)式计算得d₀=f₀=h₀=0，

因此，当k=0时，

令

其中

则ω₂₀=0，ω₁₁=0，$\left\langle {{\boldsymbol{q}}^{*}}, {{\boldsymbol{Q}}_{\boldsymbol{\tilde{q}q}}} \right\rangle =\left\langle {{\boldsymbol{q}}^{*}}, {{\boldsymbol{Q}}_{\overset{\wedge }{\mathop{\boldsymbol{q}}}\, \boldsymbol{\bar{q}}}} \right\rangle =0$.

由文献[11]可知Hopf分支的方向及其稳定性由Re(c₁(D₀))决定，其中

显然有

由文献[12]定理2.1可知：如果$\frac{1}{{\alpha }'({{D}_{0}})}\text{Re}({{c}_{1}}({{D}_{0}}))>0$，则Hopf分支的方向为次临界；如果$\frac{1}{{\alpha }'({{D}_{0}})}\ \text{Re}({{c}_{1}}({{D}_{0}}))<0$，则Hopf分支的方向为超临界；如果L(D₀)除一对共轭复根外，其他特征值均具有负实部，则当Re(c₁(D₀)) < 0时，Hopf分支渐近稳定，当Re(c₁(D₀))>0时，Hopf分支不稳定.

对于系统(5)，α′(D₀) < 0，因此当1 < j₀² < 3+2 $\sqrt{2}$时，Re(c₁(D₀)) < 0，该Hopf分支的方向次临界且周期闭轨渐近稳定；当j₀²＞3+2 $\sqrt{2}$时，Re(c₁(D₀))>0，该Hopf分支的方向超临界且不稳定.证毕.

分别针对ODE系统和PDE系统，利用Matlab软件给出数值模拟实例，验证补充理论结果.

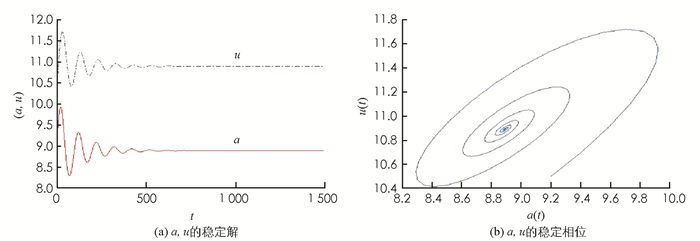
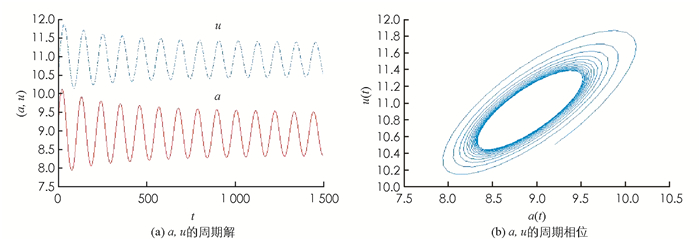
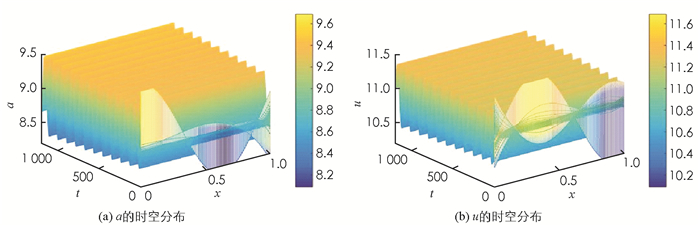
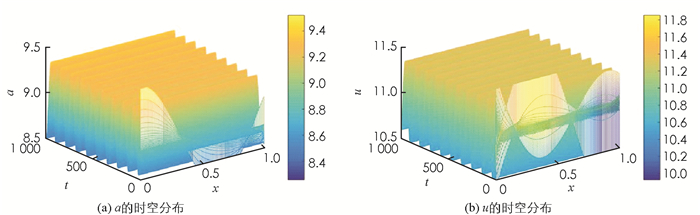
对ODE系统(2)，取T=0.045，j₀=2，D₀=0.075.若D=0.09>D₀，初始值取(a₀，u₀)=(9，10.5)时，正常数解(a^*，u^*)=(8.$\dot{8}$，10.$\dot{8}$)渐近稳定(图 1)；若D=0.074 < D₀，初始值取(a₀，u₀)=(9.2，10.5)时，在(a^*，u^*)=(8.$\dot{8}$，10.$\dot{8}$)附近产生Hopf分支，且周期闭轨渐近稳定(图 2).

初始值为(a₀，u₀)=(8+0.8cos5x，10+0.8cos5x)时，对PDE系统(5)，若取D=0.074 < D₀，D_a=1，D_u=3，则定理2中的扩散系数限定条件满足，系统(5)产生稳定的Hopf分支周期解(图 3)；若取参数D=0.074 < D₀，D_a=1，D_u=6，则定理2中的扩散系数限定条件不满足，系统(5)存在稳定的Hopf分支周期解(Matlab数值模拟见图 4).

本文针对一类电荷传输模型，分别给出ODE系统和PDE系统Hopf分支的存在性及其稳定性.结果表明，PDE系统空间齐次的周期解与ODE系统产生的周期解具有相同的稳定性条件，即1 < j₀² < 3+2 $\sqrt{2}$时，Hopf分支为次临界方向，且周期闭轨渐近稳定；当j₀²＞3+2 $\sqrt{2}$时，Hopf分支的方向超临界且不稳定.但是对于PDE系统，Hopf分支产生的条件更为严格，周期解稳定性的判定也更为困难.