Vertex-Magic Total Labelings of Some Graphs

文中S_n定义为中心节点为v₀且包含n个叶子节点的星图，扇图F_n定义为中心节点为v₀且包含n个扇页顶点的扇图.图G(p，q)表示的是包含p个顶点、q条边，且顶点集合为V(G)，边集合为E(G)的简单连通图.

定义1^[12]  对于给定的图G(p，q)，如果存在常数k和一一映射f：V(G)∪E(G)→{1，2，…，p+q}，使得对每个顶点v∈V(G)都满足f(v)+$\sum\limits_{u \in N(v)}$f(uv)=k，其中N(v)表示与顶点v所关联的顶点的集合，k为魔幻常数，则称f是图G的顶点魔幻全标号，简称VMTL，如果一个图不存在VMTL，则称其为非VMTL图，简称NVMTL.

定义2  将图G的叶子节点与图H的中心点连接，所得的图记为G▽H.例如：

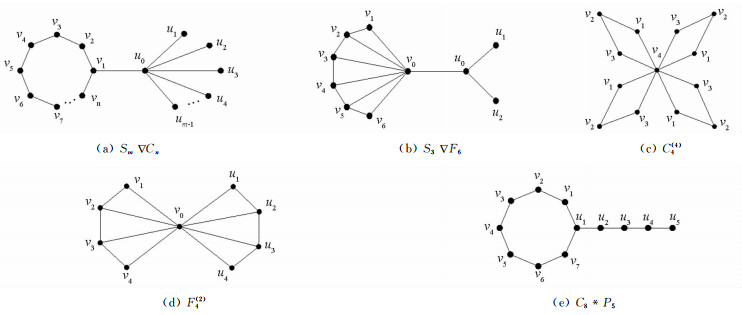
(ⅰ) G=S_m，H=C_n，联图为S_m▽C_n(n≥2，m≥3)，示例如图 1(a)所示；

(ⅱ) G=S_m，H=F_n，联图S_m▽F_n(m≥2，n≥3)，示例如图 1(b)所示.

定义3^[12]  具有公共点的m个C_n组成的图称为m个C_n的并图，记为C_n^(m)(n≥3)，示例如图 1(c)所示.

定义4^[12]  将两个扇图F_n的中心点v₀连接，即具有公共点的2个F_n组成的图，记为F_n⁽²⁾(n≥2)，示例如图 1(d)所示.

定义5^[13]  将P_k的一个端点与C_n的一个点连接，所得的图称为龙图，记为C_n*P_k，示例如图 1(e)所示.

对于给定的图G(p，q)，VMTL算法是基于搜索解空间的，进而找出VMTL，为了方便说明该算法，给出VMTL解空间φ(p，q，k)的定义：

定义6  对于度序列(d(v_i)，i=1，2，…，p)相同的一类图G(p，q)，都存在一个表(如表 1)，设u，v∈V(G)，uv∈E(G)，映射f：V(G)∪E(G)→{1，2，…，p+q}，满足f(v)，f(uv)∈[1，p+q]，f(v)+$\sum\limits_{u \in N(v)}$f(uv)=k，N(v)表示与顶点v所关联的顶点的集合，则称表 1为图G(p，q)的VMTL解空间φ(p，q，k).

对于度序列相同的一类图G(p，q)的VMTL解空间φ(p，q，k)具有如下性质：

(ⅰ) φ(p，q，k)中可以组合构造的图集合记为G^*(p，q)，其中包含连通图和非连通图，但都存在VMTL；

(ⅱ)给定图G(p，q)，若其存在VMTL，则必然包含在G^*(p，q)集合中，即解空间φ(p，q，k)具有完备性；

(ⅲ)如果图G(p，q)不包含在G^*(p，q)集合中，则它不存在VMTL.

对于图G(p，q)，当图G满足VMTL时，存在映射：f：V(G)∪E(G)→{1，2，…，p+q}，即所有的标号总和C为C=S_p+S_q=$\sum\limits_{i=1}^{p+q} i$，其中S_p和S_q分别表示点和边标号值的总和.

图G的每个顶点满足f(v)+$\sum\limits_{u \in N(v)}$f(uv)=k，即S_p+2S_q=pk.

当图G满足VMTL时，得到边和S_q、魔幻常数k的取值范围分别为

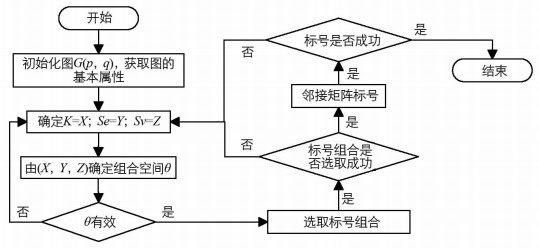
算法思路如图 2所示：

VMTL算法步骤如下：

输入：图G(p，q)的邻接矩阵文件；输出：VMTL矩阵或非VMTL图；

begin

1.读取图G的邻接矩阵AdjaMatrix

2. get p，q，degree    /*p为图点的个数，q为边的个数，degree为度序列*/

3. G.isSuccess ← false

4. C ← (p+q)(p+q+1)/2

5. for i=min；i < max；i+=p    /*min和max分别代表图G边标号之和的最小值和最大值*/

6. k ← (i + C)/p    /* k为顶点魔幻常数*/

7. get φ(p，q，k)    /* tuple(a₁，a₂，…，a_m)∈φ(p，q，k)且a₁+a₂+…+a_m=k */

8. filter by degree get φ′(p，q，k)

9. search φ′(p，q，k)

10.if(tuples → AdjaMatrix)

11.G.isSuccess ← true

12.    break

13.    end if

14.end for

15.if(graph_i.isSuccess == true)

16.        output(ResultMatrix_i)

17.    else

18.        output(AdjaMatrix)

19.end if

20.return

21.end

引理1  给定图G(p，q)，其VMTL解空间为φ(p，q，k)，用VMTL算法搜索，如果图G存在VMTL，则VMTL算法在φ(p，q，k)上一定有解，否则图G不存在VMTL.

例1  表 2为图集G(5，7)中度序列为311的图的解空间，图 3为图集中一个图的VMTL.

定理1  对于图C₄^(m)，当1≤m≤4时存在VMTL，当m≥5时不存在VMTL.

证  设V(C₄)={v₁，v₂，v₃，v₄}，即|V(C₄^(m))|=3m+1，|E(C₄^(m))|=4m，所以

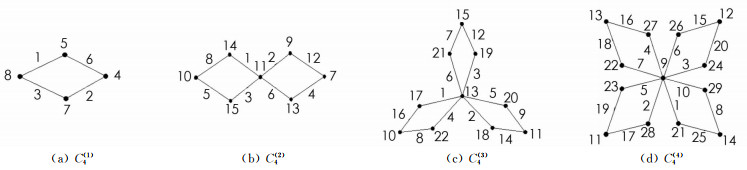
由VMTL算法得到图C₄^(m)(1≤m≤4)的VMTL如图 4所示：

对于图C₄^(m)，k取最小值时，图C₄^(m)的最大度点以及其关联边取最小标号值

k取最大值时，C₄^(m)中2m条边加两次，即$3 m k \leqslant \sum\limits_{2}^{7 m+1} i+\sum\limits_{5 m+2}^{7 m+1} i=\frac{1}{2}\left(73 m^{2}+27 m\right)$.

可得2m²+3m+1≤$\frac{1}{2(3 m)}$(73m²+27m).由12m²-55m-21≤0，得到1≤m≤4，所以，定理1成立.

定理2  对于图F_n⁽²⁾，当2≤n≤4时存在VMTL，当n≥5时不存VMTL.

证  设扇图F_n的顶点集合V(F_n)={v₀，v₁，v₂，…，v_n}，即|V(F_n⁽²⁾)|=2n+1，|E(F_n⁽²⁾)|=4n-2，所以f(V(F_n⁽²⁾))∪f(E(F_n⁽²⁾))→{1，2，…，6n-1}.

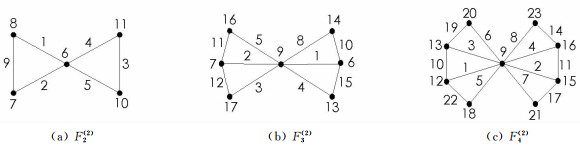
由VMTL算法得到图F_n⁽²⁾(2≤n≤4)的VMTL如图 5所示：

k取最小值时，图F_n⁽²⁾的最大度点以及其关联边取最小标号值，即

k取最大值时，图F_n⁽²⁾中边缘n-1条边加两次，所以取最大标号值，即

可得2n²+3n+1≤$\frac{1}{2 n}$(28n²-12n-2)，2n³-11n²+7n+1≤0，得到1≤n≤4.所以，定理2成立.

定理3  对于图C₃*P_k，当2≤k≤14时存在VMTL.

证  设V(C_n)={v₁，v₂，…，v_n}，V(P_k)={u₀，u₁，u₂，…，u_k}，即|V(C_n*P_k)|=n+k-1，|E(C_n*P_k)|=n+k-1，所以f(V(C_n*P_k))∪F(E(C_n*P_k))→{1，2，…，2n+2k-2}.

k取最小值时，图C_n*P_k的最大度点以及其关联边取最小标号值k≥10；

k取最大值时，C_n中n条边加两次，所以C_n中n-2条边取最大值，P_K的k-1个顶点以及其关联边取次大标号值，即

可得10≤$\frac{7 k^{2}+7 n^{2}+14 k n-17 n-17 k-4}{2(n+k-2)}$，7k²+(14n-37)k+7n²-37n+36≥0，得到k≥-n+4.当n=3时，k≥1，图C₃*P_k可能存在VMTL.

由VMTL算法得到图C₃*P_k(2≤k≤14)的VMTL如表 3所示：

所以，定理3成立.

猜想1  对于C_n*P_k，当n≥3，k≥2时存在VMTL.

定理4  对于图S_m▽C₃，当1≤m≤3时存在VMTL，当m≥4时不存在VMTL.

证  设V(C_n)={v₁，v₂，…，v_n}，V(S_m)={u₀，u₁，u₂，…，u_m}，即

所以f(V(S_m▽_n))∪F(E(S_m▽_n))→{1，2，…，2n+2m}.

k取最小值时，u₀和v₁点及其关联边取小标号值，边u₀v₁加两次，所以f(u₀v₁)取最小值1，即

k取最大值时，C_n中n-2条边加两次，所以C_n中n-2条边取最大值，S_m的m-1个叶子节点以及其关联边取次大标号值，即

可得$\frac{1}{4}$(m²+9m+22)≤$\frac{4 m^{2}+7 n^{2}+12 m n-6 m-n-18}{2(m+n-2)}$，m³-m²+m²n-15mn+16m-14n²+24n-8≤0.当n=3时，有m³+2m²-29m-62≤0，得到-2≤m≤5.所以，当m≥6时，图S_m▽C₃不存在VMTL.

图S_m▽C₃(1≤m≤3)的VMTL如图 6所示：

对于图S₄▽C₃，|V(S₄▽C₃)|=7，|E(S₄▽C₃)|=7，所以f(V(S₄▽C₃))∪f(E(S₄▽C₃))→{1，2，…，14}.根据引理1，在解空间φ(7，7，k)中执行VMTL算法得出该图不存在VMTL.同理，可得图S₅▽C₃不存在VMTL.

综上所述，定理4成立.

定理5  对于图S₂▽F_n，当2≤n≤8时存在VMTL，当n≥9时不存在VMTL.

证  设扇图F_n的顶点集合V(F_n)={v₀，v₁，v₂，…，v_n}，V(S₂)={u₀，u₁，u₂}，|V(S_m▽F_n)|=n+3，|E(S_m▽F_n)|=2n+1，f(V(S_m▽F_n))∪f(E(S_m▽F_n))→{1，2，…，3n+4}.

k取最小值时，v₀点及其关联边取最小标号值，即

k取最大值时，扇图F_n中n-1条边加两次，所以取最大标号值，即

可得$\frac{1}{2}$(n²+5n+6)≤$\frac{14 n^{2}+32 n+8}{2(n+2)}$，即n³-7n²-16n+4≤0，得到0≤n≤8.

由VMTL算法得到图S₂▽F_n(2≤n≤8)的VMTL如表 4所示：

所以，定理5成立.

图的VMTL自提出以来，已有很多特殊图的标号结论，由于图数量庞大，利用手工标号找出图的标号规律局限于特殊图，即通过对点数少的一类图进行标号，发现标号规律，然后验证点数多的该类型图是否满足该规律，但是这种方法无法找出一般图的标号规律.

本文给出一种针对顶点魔幻解空间的递归搜索VMTL算法，利用VMTL的特性以及一系列剪枝函数对其进行优化，对整个解空间进行搜索遍历.该算法可以对有限点内的所有图进行标号，得出该图是否存在VMTL，然后从结果集中分析标号结果，找到龙图、图C₄^(m)、图F_n⁽²⁾以及联图G▽H的标号规律，总结出若干定理.