Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2020 Volume 45 Issue 9
Article Contents
Previous Article Next Article

Yu WU, Mao-ling PENG, Ren-fei QIAN, et al. An Intrusion Detection Model Based on Nonnegative Matrix Factorization Optimized by Genetic Programming[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(9): 139-146. doi: 10.13718/j.cnki.xsxb.2020.09.021
Citation: Yu WU, Mao-ling PENG, Ren-fei QIAN, et al. An Intrusion Detection Model Based on Nonnegative Matrix Factorization Optimized by Genetic Programming[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(9): 139-146. doi: 10.13718/j.cnki.xsxb.2020.09.021
shu

An Intrusion Detection Model Based on Nonnegative Matrix Factorization Optimized by Genetic Programming

  • 1.

    Chongqing Police College, Chongqing 401331, China

  • 2.

    Chongqing City Management College, Chongqing 401331, China

  • 3.

    Ningbo Dafa Chemical Fiber Company Limited, Ningbo Zhejiang 315336, China

  • 4.

    College of Computer and Information Science, Southwest University, Chongqing 400715, China

More Information
  • Corresponding author: Mao-ling PENG ; 
  • Received Date: 16/11/2019
    Available Online: 20/09/2020

  • MSC: TP393.0

  • In the paper, nonnegative matrix factorization has been used to detect privileged program behavior of system monitoring, and then abnormal intrusion behavior been found. In the process of matrix factorization, Alpha-divergence is used as the measurement standard, and genetic programming algorithm is introduced to optimize the error function in non-negative matrix factorization. In the experiment, we have tested the system call data obtained from the Sun SPARC workstation of the University of New Mexico and CICIDS2017 data set. The experiment results show that our method has good performance in intrusion detection for detection accuracy.
  • 加载中
  • [1] 席荣荣, 云晓春, 张永铮, 等.一种改进的网络安全态势量化评估方法[J].计算机学报, 2015, 38(4): 749-758.

    Google Scholar

    [2] JAJODIA S, ALBANESE M. An Integrated Framework for Cyber Situation Awareness [J]. Theory and Models for Cyber Situation Awareness, 2017, 10030: 29-46

    Google Scholar

    [3] LOUKAS G, VUONG T, HEARTFIELD R, et al. Cloud-Based Cyber-Physical Intrusion Detection for Vehicles Using Deep Learning [J]. IEEE Access, 2018, 6(1): 3491-3508.

    Google Scholar

    [4] AHMADIAN RAMAKI A, RASOOLZADEGAN A, JAVAN JAFARI A. A Systematic Review on Intrusion Detection Based on the Hidden Markov Model [J]. Statistical Analysis and Data Mining: the ASA Data Science Journal, 2018, 11(3): 111-134. doi: 10.1002/sam.11377

    CrossRef Google Scholar

    [5] 高妮, 高岭, 贺毅岳, 等.基于自编码网络特征降维的轻量级入侵检测模型[J].电子学报, 2017, 45(3): 730-739.

    Google Scholar

    [6] 徐慧敏, 陈秀宏.图正则化稀疏判别非负矩阵分解[J].智能系统学报, 2019, 14(6): 1217-1224.

    Google Scholar

    [7] MENG Y, SHANG R H, JIAO L C, et al. Feature Selection Based Dual-Graph Sparse Non-Negative Matrix Factorization for Local Discriminative Clustering [J]. Neurocomputing, 2018, 290: 87-99. doi: 10.1016/j.neucom.2018.02.044

    CrossRef Google Scholar

    [8] 钟琴.非负矩阵最大特征值的新界值[J].西南大学学报(自然科学版), 2018, 40(2): 40-43.

    Google Scholar

    [9] LIAO Q, ZHANG Q. Local Coordinate Based Graph-Regularized NMF for Image Representation [J]. Signal Processing, 2016, 124: 103-114. doi: 10.1016/j.sigpro.2015.09.038

    CrossRef Google Scholar

    [10] LEE D D, SEUNG H S. Learning the Parts of Objects by Non-Negative Matrix Factorization [J]. Nature, 1999, 401(6755): 788-791. doi: 10.1038/44565

    CrossRef Google Scholar

    [11] CICHOCKI A, ZDUNEK R, AMARI S I. Csiszár's Divergences for Non-Negative Matrix Factorization: Family of New Algorithms [M]//Independent Component Analysis and Blind Signal Separation. Berlin: Springer, 2006: 32-39.

    Google Scholar

    [12] CICHOCKI A, CRUCES S, AMARI S I. Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization [J]. Entropy, 2011, 13(1): 134-170. doi: 10.3390/e13010134

    CrossRef Google Scholar

    [13] DHILLON I S, SRA S. Generalized Nonnegative Matrix Approximations with Bregman Divergences [J]. Advances in Neural Information Processing Systems, 2005(11): 5-8.

    Google Scholar

    [14] 荣德生, 段志田, 胡举爽, 等.基于二阶锥规划与改进遗传算法的配网重构[J].控制工程, 2019, 26(2): 223-228.

    Google Scholar

    [15] 李建国, 张海飞, 周璐婕, 等.基于改进遗传算法的立体车库布局对比及服务资源优化[J].西南大学学报(自然科学版), 2019, 41(4): 139-148.

    Google Scholar

    [16] BENJAMIN R, BARTLEY R. Sequence Aggregation Rules for Anomaly Detection in Computer Network Traffic [C]//American Statistical Association 2018 Symposium on Data Science and Statistics. Berlin: Springer, 2018: 1-13.https://www.researchgate.net/publication/325226141_Sequence_Aggregation_Rules_for_Anomaly_Detection_in_Computer_Network_Traffic

    Google Scholar

    [17] VIJAYANAND R, DEVARAJ D, KANNAPIRAN B. Intrusion Detection System for Wireless Mesh Network Using Multiple Support Vector Machine Classifiers with Genetic-algorithm-based Feature Selection [J]. Computers & Security, 2018, 77: 304-314.

    Google Scholar

    [18] NICHOLAS L, OOI S Y, PANG Y H, et. al. Study of Long Short-Term Memory in Flow-Based Network Intrusion Detection System [J]. Journal of Intelligent & Fuzzy Systems, 2018, 35(3): 1-11.

    Google Scholar

    [19] SHARAFALDIN I, HABIBI LASHKARI A, GHORBANI A A. Toward Generating a New Intrusion Detection Dataset and Intrusion Traffic Characterization [C]//Proceedings of the 4th International Conference on Information Systems Security and Privacy. Funchal: Science and Technology Publications, 2018: 1-18.https://www.researchgate.net/publication/322870768_Toward_Generating_a_New_Intrusion_Detection_Dataset_and_Intrusion_Traffic_Characterization

    Google Scholar

    [20] KUMAR N, MALLICK P. Blockchain Technology for Security Issues and Challenges in IoT [J]. Procedia Computer Science, 2018, 132: 1815-1823. doi: 10.1016/j.procs.2018.05.140

    CrossRef Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(4)  /  Tables(4)

Export Citation
PDF
XML

Article Metrics

Article views(1173) PDF downloads(97) Cited by(0)

Access History

Other Articles By Authors

An Intrusion Detection Model Based on Nonnegative Matrix Factorization Optimized by Genetic Programming

    Corresponding author: Mao-ling PENG ; 
  • Received Date: 16/11/2019
  • Available Online: 20/09/2020

Abstract: In the paper, nonnegative matrix factorization has been used to detect privileged program behavior of system monitoring, and then abnormal intrusion behavior been found. In the process of matrix factorization, Alpha-divergence is used as the measurement standard, and genetic programming algorithm is introduced to optimize the error function in non-negative matrix factorization. In the experiment, we have tested the system call data obtained from the Sun SPARC workstation of the University of New Mexico and CICIDS2017 data set. The experiment results show that our method has good performance in intrusion detection for detection accuracy.

    HTML

  • 入侵检测可以在恶意攻击发生时或发生后直接检测到它们.它可以从网络或计算机系统的某个节点收集流量或系统调用等信息，分析和判别数据特征，进而区分正常和异常行为，从而实现对网络的保护[1-2].一般来说，入侵检测系统需要处理大量的数据，这些数据可能包含一些不相关和冗余的特性，这些特性会减慢训练和测试过程，增加资源消耗，降低检测率.特征选择是入侵检测系统的核心内容之一[3]，从网络数据中提取正常或异常特征是自动生成入侵特征的最有效方法之一.如果特征知识能够被恰当地提取和表达出来，还可以预测新的攻击[4].特征提取可以有效地降低计算维数，加快入侵检测进程[5].本文提出了一种通过监控特权程序行为来检测入侵行为的方法，为了建立异常检测模型，考虑了系统调用的特征，然后，这些系统调用被按照一定长度进行序列化，以生成数据向量来训练分类器.在此基础上，利用非负矩阵分解(nonnegative matrix factorization，NMF)模型来分析特权程序的正常和异常行为，结合Alpha散度来度量迭代分解过程中的差异程度，并利用遗传算法优化非负矩阵分解中的误差函数，以此来提升检测的精度.

1.   基于非负矩阵分解的入侵检测

  • 非负矩阵分解方法的一个优点是计算效率较高[6-7].基于NMF的模型对系统调用的分析可以避免对单个程序调用序列进行训练，降低了学习过程的计算成本[8-9].本文利用系统调用序列中的特征向量构建NMF模型的输入矩阵.通过矩阵非负分解得到基矩阵，以此来创建程序的行为特征，从而构建起特征库.计算需要检测的测试向量与其重建矩阵之间的距离，并与阈值进行比较，以确定是否存在异常行为.

    • 1.1.   非负矩阵分解

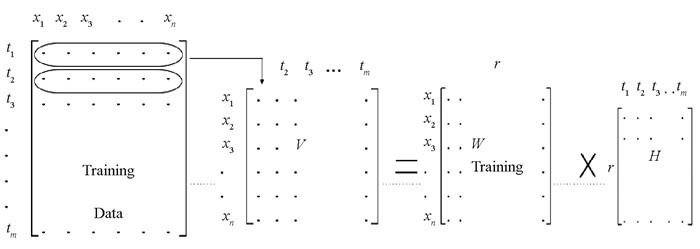
  • 在文献[10]中引入了非负矩阵因式分解方法，寻找非负部分的数据表示.给定一个非负矩阵V，寻找非负矩阵因子W和H，使得

    其中W是一个m×r的矩阵而H是一个r×n的矩阵. (1)式也可以按照列相乘的方式写为vi≈Whi，vi和hi分别表示V的第i列和H的第i列向量，也即矢量vi是W的列与权重hi的线性组合. W的列可以表示基向量，且当与适当的混合权重(H的某列)组合时，将得到V的线性近似值.

    • 1.2.   基于Alpha散度的误差度量

  • 非负矩阵在分解过程中通过不断迭代产生近似的基矩阵W和权矩阵H，其分解过程中度量差异程度的指标采用Kullback-Leibler(KL)散度[11]. KL散度常用于计算两个概率分布P和Q的差异，表示当用概率分布Q来拟合真实分布P时产生的信息损耗，在非负矩阵分解中用来度量V与WH的差异.但KL散度无法对分解过程进行稀疏约束，而通常系统调用数据很大程度上是稀疏数据，导致分解过程有可能收敛到局部最优值，因此引入Alpha散度作为度量标准. Alpha散度属于凸散度集，该散度集属csiszár散度集，也称Ali-silvey散度[12-13].所以本文考虑基于Alpha散度的NMF的目标函数，它被用于度量V与WH之间的差异，其定义为

    (2) 式的Alpha散度通常可以表达为

    其中$ \beta = \frac{{1 + \alpha }}{2}$.事实上，我们可以通过多种方式对Alpha散度进行平滑或稀疏约束，以增强Alpha散度的数据特征表达能力.本文引入了一个带正则项的修正Alpha散度

    其中：αs≥0是正则化参数；引入项J(H)和J(W)用来强化依赖于应用的特性，如光滑性或稀疏性[14]，这里

    为了得到稀疏表达，通常选择f(xj)=xj或者f(xj)=xjlog(xj)，xj≥0，因此，J(H)和J(W)沿用了式(6)定义.对(5)式应用梯度下降方法，得到非负矩阵分解的乘性迭代规则

    其中：wij≥0，hjk≥0，∀ i，j，k∈ $ \mathbb{N}$.在每一步迭代中wij将被正则化：

    这里ω∈ (0，2)是过松弛参数.本文应用非线性变换xjk=(xjk)1+αs，其中αs是一个取值较小的系数，通常取值在0.001与0.005之间.如果想增加计算过程中的稀疏性，取正值；如果想减少稀疏性，取负值.类似于Alpha散度，还设计了Jensen-Shannon散度乘法迭代规则(β=2)，Hellinger散度的乘法迭代规则(β=0.5)，这些规则在稀疏性和松弛性方面施加了额外的约束.

    • 1.3.   基于非负矩阵分解的入侵检测

  • 本文以系统命令调用序列和系统访问记录为数据源，对入侵行为进行分析.利用非负矩阵分解方法建立系统调用行为的检测及分析模型.通过方程(7)，(8)，(9)给出的规则把V分解为两个矩阵Wtraining和H.矩阵W训练的每一列都包含一个基向量，而H的每一列表示V中对应列所需的系数.

    事实上，对于等式vi≈Whi，v和h分别对应V和H的列向量.每个向量v由w列的线性组合来逼近，而w列的加强分量为h.基于此，对于测试矩阵Vtest(由测试数据构成)的列向量而言，使用从规一化训练数据中得到的基Wtraining，通过迭代更新规则(10)能够找到编码系数的表示向量h，然后重构v得到v’

    然后利用式(5)计算两个向量之间的相似性

    如果测试数据是归一化的，则通过式(10)重构的v’与v非常相似，λ较小.测试数据向量是否正常可以通过λ与阈值的比较来进行判别.当λ < ε时为正常行为，否则分类为异常行为，其中ε为阈值，这是一个二分类问题.整个入侵检测的判断过程被分为如下三个步骤：

    步骤1：在训练阶段找到用Ahpha散度来度量NMF的最佳参数，如β，ω，αs，然后将寻优问题转化为多峰函数优化过程，进一步针对入侵检测模型，应用遗传规划算法来获取β，ω，αs的最佳值.

    步骤2：在最佳的β，ω，αs参数状态下，用训练数据建立基于NMF的学习模型.利用训练集构建矩阵V，通过式(7)，(8)的矩阵分解得到Wtraining及对应系数H.

    步骤3：利用相应的乘法学习规则对测试数据进行分解，然后进行重构，利用式(11)对入侵过程和正常过程进行分类.

2.   利用遗传规划对基于NMF的入侵检测方法进行优化

  • 遗传算法是一类基于进化和自然选择原理的计算模型.这些算法通过使用类似染色体的数据结构将特定域中的问题转换为模型，并使用选择、重组和变异算子进化染色体[14-15].本文利用遗传算法分别得到非负矩阵分解中的β，ω，αs等参数，也即利用遗传算法学习和优化非负矩阵分解的入侵检测模型.具体的实现过程如下：

    1) 读入非负矩阵分解迭代方程；

    2) 读入任务参数{β，ω，α}；

    3) 读入GP参数：种群规模(pS)、最大进化代数(Gmax)、遗传算子GO集合、遗传算子概率因子向量PGO；

    4) 根据{β，ω，α}构造种群规模为pS的初始群体；

    5) 计算每个个体染色体的适应度函数，保存最好的个体；旋转赌轮选择pS个个体作为父代；对父代按照遗传算子执行进化操作以产生新一代群体；将新一代群体代替当前群体；重复上述过程，直至进化代数达到Gmax；

    6) 返回最好个体的染色体以得到非负矩阵分解中的最佳参数β，ω，αs.

    该算法核心是将遗传规划方法应用于基于非负矩阵分解迭代方程式中，其中每个个体的染色体用变长的层次结构来表示一组参数组合方案.算法通过对群体的多个个体执行进化操作以促进群体的进化，并利用适应度函数作为启发信息来指导算法朝规划的优化方向发展.

3.   实验与分析

    3.1.   数据分析

  • 收集了几个由活动进程执行的系统调用数据集.这些程序的大小和复杂性因不同的入侵方式(缓冲区溢出、符号链接攻击和特洛伊木马程序)而有很大的不同.每个跟踪是单个进程从执行开始到结束发出的系统调用的列表.为了评估所提出的异常检测方法，在实验中使用了两组系统调用数据来分析程序行为.

    • 3.1.1.   sendmail的调用指令集合

  • 实验数据来源于UNM集合中关于sendmail的调用指令，可以从http://www.cs.unm.edu获得.跟踪系统调用的指令列表从UNM的Sun SPARC工作站上得到，该工作站运行的系统为SunOs4.1.1和4.1.4.使用plus表示正常调用的数据，建立调用长度为k=6的序列长度数据库.例如，观测到入侵系统调用序列：

    考虑在SunOS 4.1x操作系统中执行这个任务需要182个系统调用，每一个系统调用被分配的任务号从1到182，系统调用的路径可以表示为数字序列：

    由于设定序列长度为6，得到3组对应的系统调用序列：

    实验中，测试数据包含正常数据“bounce”，“bounce-1”，“bounce-2”和“queue”，以及异常数据“sm-280”，“sm-314”，“sm-10763”，“sm-10801”，“sm-10814”.构建长度为k=6的系统调用序列数据库.利用非负矩阵分解进行异常检测时，在训练阶段从数据库中调用序列构建起矩阵V，通过迭代分解得到矩阵Wtraining和H，检测阶段利用未知序列构建矩阵进行分解得到系数向量h，通过Wtraining×h重构v’，再与v比较就可以判断是否存在异常调用.

    • 3.1.2.   CICIDS2017数据集

  • 加拿大网络安全研究所提供了一个名为CICIDS2017的最新数据集，包含最新的威胁和特性.该数据集吸引全球的研究人员来分析和开发新的模型和算法[16-18]，是当前比较全面的网络安全测试数据集.该数据集包含8个子集[19].

    该数据集拥有11个特征，即匿名性、攻击多样性、完全捕获、完全交互、完全网络配置、可用协议、完全流量、特征集、元数据、异构性和标签[20]. CICIDS2017集合有8个文件，共计2 830 743条记录，每条记录有79个类别.每一记录行被标记为正常(Normal)或14种攻击类型之一. 表 1总结了不同攻击类型和正常行为的分布情况.

    根据表 1中描述的数据分布提取训练和测试子集.在每个子集中，我们试图包含所有攻击的样本，但是不能在两个子集中出现相同的记录.提取数据集中每种类型的第一条记录组成训练子集.在抑制训练子集中随机选择记录组成测试记录.

    • 3.2.   结果分析

  • 使用召回率Precall、精确率Pprecision、假阳性率pFPR和假阴性率pFNR作为指标来评估算法的性能.

    其中：CTP指正确分类的正样本数，表示根据公式(9)正确判断为异常事件的数量；CFP指被错误标记为正样本的负样本数，表示根据公式(9)判断为异常事件的正常事件数；CTN指正确分类的负样本数，表示根据公式(9)正确判断为正常事件的数量；CFN指被错误标记为负样本的正样本数，表示根据式(9)判断为正常事件的异常事件数.

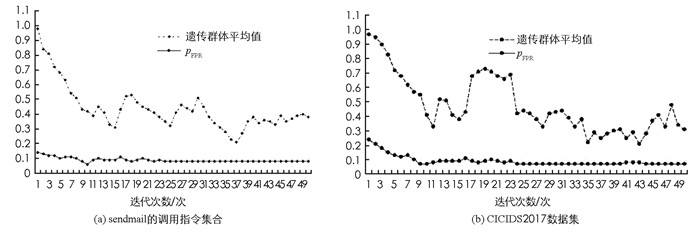
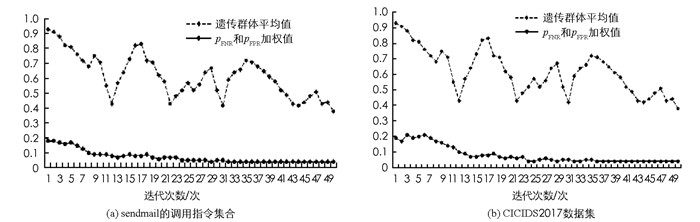
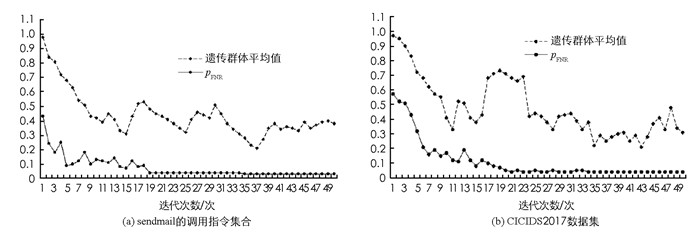
    图 1为对sendmail的调用指令集合与CICIDS2017数据集的50次迭代过程中pFPR值和遗传群体平均值的变化曲线. 图 2为对sendmail的调用指令集合与CICIDS2017数据集的50次迭代过程中pFNR和遗传群体平均值的变化曲线.可以看到在两种数据集下，遗传群体平均值逐渐趋于平稳，说明本文所提算法随着迭代次数的增加而收敛；同时pFNR和pFPR也稳定到最小值.显然，pFPR和pFNR的最优值是不同的.为了找到最合适的参数，对pFPR和pFNR进行了加权，pFPR和pFNR加权值的变化曲线如图 4所示.由图 3可知，加权最优值为0.048(pFPR=0.02，pFNR=0.028)，参数β=2，ω=0.45，αs=0.032.

    图 4用召回率Precall、精确率Pprecision曲线展示了遗传群体平均值对检测的影响.可以看出，pFPR和pFNR进行加权后，sendmail数据集召回率稳定在0.93，精确率稳定在0.96；CICIDS2017数据集召回率稳定在0.92，精确率稳定在0.94.

    为了进一步评估Alpha-NMF模型的参数精度，将Alpha-NMF，PCA，HMM以及标准的NMF进行了对比测试(表 2)，其中：异常检测率是指检测出的异常行为数量与样本所有异常行为数量的比率；正常检测率是指检测出的正常行为数量与样本所有正常行为数量的比率.

    从表 2可以看出，在sendmail的调用指令集合和CICIDS2017数据集中，Alpha-NMF的异常检测率和正常检测率都高于其他方法.相对于PCA和HMM方法，本文的方法无论是对异常行为的检测还是正常行为的判断，其性能都有10%左右的提升.此外，还观察到当β=0.5，ω=0.3，αs=0.02或β=2，ω=0.26，αs=0.017时，本文方法性能稍差.当β=2，ω=0.45，αs=0.032时，Alpha-NMF能够得到全局最优解，使得本文方法在sendmail集合中达到最佳检测率为90.5%和94.3%.在CICIDS2017数据集中，最佳检测率为91.2%和93.3%.同时，实验还对比了训练和检测的时间开销，从表 3和表 4中可以发现，本文提出的方法在训练时间上高于其他3种方法，特别是在CICIIDS2017数据中，参数为β=2，ω=0.26，αs=0.017时，训练时间高达44 s，这是因为矩阵分解过程迭代次数较多，而遗传算法在参数优化的过程中需要较多的时间进行计算，但模型参数一旦优化后，利用生成的模型进行检测时，检测速度就能得到较大提高.

4.   结论

  • 本文提出了一种应用遗传算法求解Alpha-NMF全局最优解的方法并用于入侵检测中.为了确保矩阵分解过程的全局最优化，采用了Alpha散度来约束迭代更新规则，以实现最小化观测数据和模型之间的差异.实验证明，Alpha-NMF的迭代更新方式在入侵检测问题上是有效的，但它的学习过程较慢，因此，遗传算法可以用来寻找全局最优参数，这大大提高了检测方法的性能.

Figure (4)  Table (4) Reference (20)

Catalog

    Copyright Journal of Southwest China Normal University(Natural Science Edition)

    Address： Tel：023-68252540，68254576，68254478 E-mail：xbbjb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return