On Prediction Algorithm of Blackout Sensitivity Based on Characteristics of Power Customer Clustering

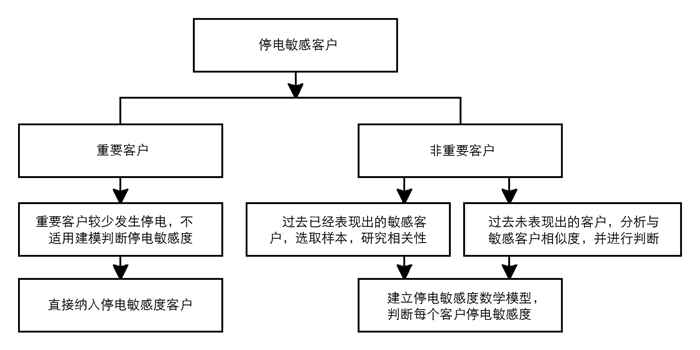
客户停电敏感度研究是通过对不同客户行为特征进行分析，从而将其对停电敏感程度的差别反映出来，并通过数据挖掘技术量化手段分析停电敏感客户^[10].在研究过程中，针对不同客户，即采用分类考虑方式，对非重要客户、重要客户停电敏感度分别进行分析，图 1为客户停电敏感度研究思路.

以客户停电敏感行为为样本，分析其在停电期间的主要特征，并更多地提取可能客户的信息字段，最后由数据挖掘算法来构建非重要客户对停电敏感的预测模型.通过模型可以模拟客户未来行为的概率.概率越高，客户对停电越敏感.

如果该客户在一个地区或国家的政治、社会、经济生活中占有比较重要的地位，如果对其停电将影响政治、可能发生较多人身伤亡、严重的经济损失和环境污染、甚至是社会公共秩序严重混乱的用电单位，或对供电有特殊要求的用电场所，就称其为重要客户.因重要客户具有特殊的身份，这些客户对电力供应具有很高的要求，电力企业通常会通过双回路、保供电、双电源供电等方式，确保停电不会发生; 同时因为被停电较少，客户行为对客户敏感度无法反映，因而可将其纳入停电敏感度高的客户.

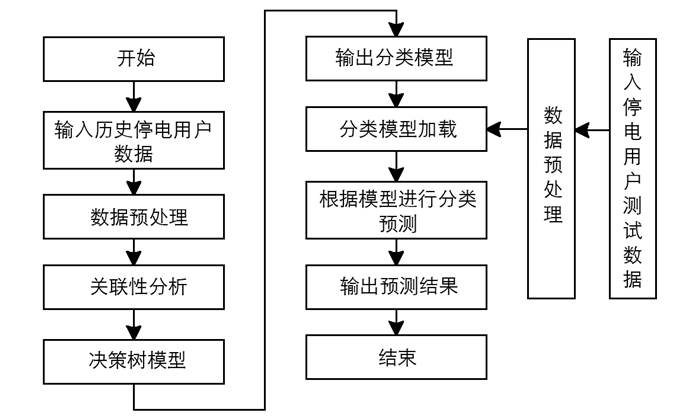
图 2为停电敏感度分析流程图，在分析用户进行停电敏感度时，采用决策树方法，主要包括特征选取、数据预处理、停电敏感度分析模型的构建等.

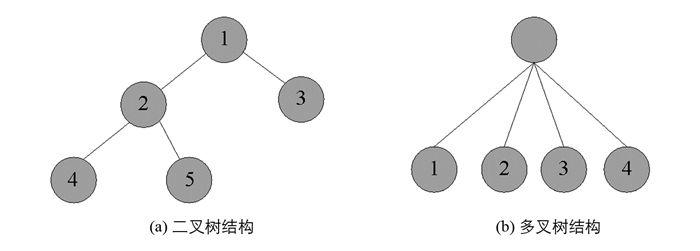
决策树模型是机器学习中一种常见的模型，以树模型为核心分类器.每对变量进行一次测试就会在决策树内部增加一个节点，每次的测试结果由决策树中的树枝来代替，每个分支表示一个测试结果，如果想要某一类的分布情况就用叶节点来表示.通常决策树过程的计算从根节点开始，然后将计算出的数据与决策树中的特征节点进行比较，从而得到下一分支的数据，当叶子节点作为结果时停止.二叉树、多叉树为其组成的基本结构，图 3所示.判别对停电敏感时，由于与多叉数相比二叉树的分析能力较差，所以本文采用了多叉树分析方式.将带有标签的一组目标变量输入决策树中，通过从上到下递归分割的方法构造决策树，从根节点开始，选择一个变量，分析变量取值将数据集分为多个子集合，再用递归的方法处理各个子集，直到完成整个分类过程.

在多叉树结构中，每个测试条件都可以由决策树中的一个节点来表示，决策树被这个测试条件分为多个分支，测试条件的每个可能答案都由每个分支来表示.在本文中，将Y设置为仅取0和1两个值，用1代表符合停电敏感客户定义目标，用0代表设定的其余客户目标，与此同时设定重要算法参数规则:设置7个非居民建模、9个居民建模，在拆分过程中仅使用一次; 采用多叉树方法设定2为最大分支数; 最小类别大小为5，也就是每层记录数最小为5; 6为最大深度，也就是规则最多为6层; 运用统计量拆分规则，将相应统计量最大变量找出并作为拆分准则.本研究采用的决策树算法为CHAID算法.

CHAID指卡方相互自动检验，检验卡方CHAID的分割选择和算法使用还是和逐步回归方法相似.就是搜索某个变量X，分割某个节点，开始时分为两个或以上的子节点，而变量类型则决定着数量. CHAID识别包括不缺失值、分类、缺失值.若X属于着分类，那么分割一个节点t，这样，所有X类别的子节点就形成了; 若X属于着单调，那么就将t分割成10个子节点，由一个X值区间定义每个子节点; 若X属于着浮动，那么将t分成10个子节点，并添加一个缺失值.最后由测试Bonferroni和p值对显著性进行调整，测试合并子节点，并把合并的子节点当成分区，采用Bonferroni调整测试.每个X变量p值全部使用Bonferronir来调整，利用最小p值拆分该节点.要实现合并、拆分、终止，可以使用CHAID算法.

要对所有变量X进行预测，需要合并非重要类别.如果以X分割节点，那么最终每个子节点将由X类别产生.在分裂步骤中还需对调整后的p值进行计算使用.步骤一是若X类别只有一个，停止同时设置p=1.步骤二是若X有类别两个，则进入步骤八.步骤三是在X允许类别找到后，测试统计量给出相关变量最大p值.步骤四是拥有最大p值一对，对其p值是否大于用户指定级进行检查，若是，则将此对合并为单一复合类别，形成一组新X类别，若无，则转到步骤七.步骤五是若包含大于3个原始类别的复合类别，那么在p值最小复合类别内分割最佳二进制; 若级的分裂合并大于或等于此p值，那么将此二进制文件分割.步骤六是转到步骤二.步骤七是次数少的类别与最相似其他类别合并.步骤八是对p值调整，应用Bonferroni调整对合并的类别进行计算.步骤九是次数太少的类别与最相似的其他类别合并.

预测器最适合的拆分可在合并过程中找到，那么最佳分割节点预测器的选择，就是拆分步骤.而选择则需要对所有预测器p值比较，p值在合并步骤中调整得到，选择最小p值的预测器.若用户指定级拆分小于p值，那么就用此节点，不然此节点是终端节点，步骤中止，检查决策树生长过程的正误，若一个节点纯净，则节点中全部情况的因变量值相同，不会分割节点.若当前决策树深度达到用户指定最大深度限值，在生长过程停止.若节点大小要比用户指定最小节点大小值小，则不会拆分节点，若一个节点子节点太少，则与最相似子节点合并，若子节点结果数量为1，则不会分割节点.

决策树模型里，假如因变量Y是连续的，那么就分析方差，测试不同类别X的Y相不相同，通过方差分析，计算F统计值获得p值，具体见如下公式:

其中，$ \bar{y}=\frac{\sum\limits_{n \in D} w_{n} f_{n} y_{n}}{\sum\limits_{n \in D} w_{n} f_{n}}, \bar{y}_{i}=\frac{\sum\limits_{n \in D} w_{n} f_{n} y_{n}\left(x_{n}=i\right)}{\sum\limits_{n \in D} w_{n} f_{n}\left(x_{n}=i\right)}, N_{f}=\sum\limits_{n \in D} f_{n}, F\left(I-1, N_{f}-I\right)$是个随机变量，并且，f分布的要求满足自由度是I和N_f－1.

若因变量Y是名义范畴时，那么，检验X和Y独立零假设，Y类是列，X类是行，因此，得到偶然性表用来测试，且估计零假设下的期望频率.可利用皮尔逊卡方统计或似然比统计来计算观察频率及期望频率.通过此两个统计数据中随意一个来计算p值，公式(3)为皮尔逊卡方统计方程，似然比统计量见公式(4):

其中，为对$ n_{i j}=\sum f_{n} I\left(x_{n}=i \wedge y_{n}=j\right)$的频率进行观察，在独立模型中，对$\left(x_{n}=i, y_{n}=j\right) $的预期频率进行估计，从而得到相应p值，具体见公式(5):

其中，$x_{d}^{2} $达到自由度为d=(J－1)(I－1)的卡方分布要求，$ {{\overset{\wedge }{\mathop{m}}\, }_{ij}}={{n}_{i}}{{n}_{j}}/n$表示无权重估计频率.

对可能与停电敏感度相关客户信息字段进行选取，分别是计量方式、电压等级、停电时长、用电类别、停电次数、营业区域、电源类型等20个字段，预处理数据的清洗、二次计算等预处理也在同时进行，且以此当做建模因素筛选的首要输入变量.

之所以使用决策树数据挖掘算法，然后对建模字段的数据进行建模、验证，是由于此研究是分析并预测客户未来的行为概率.为满足建立模型的要求，将所采集的样本数据按45%，35%，15%随机地离散成验证集、训练集、测试集.训练集用于数据建模、模型验证，根据验证设置、调整和模型结果通过测试组进行测试.在这项研究中，以广东省某市供电局145.2万个客户为研究目标.在此之中，有非居民客户24.4万，居民客户120.8万，样本数据变量从所有客户中随机抽取，比例为35%.即非居民客户样本8.54万，居民客户样本42.28万来建模数据.数据分析的同时，利用SAS Enterprise Miner Server软件来数据建模.

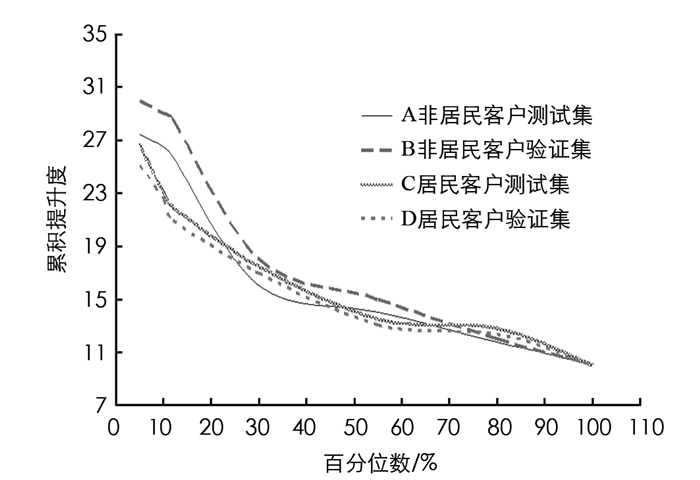
用决策树CHAID算法根据训练集的样本客户对相应的客户停电敏感度模型进行构建，通过对验证集的样本用户试用此模型，然后更好地调整和完善改进此模型，并且构建相应的预测模型.在测试集客户上进行应用决策树CHAID算法模型，并且将测试集、验证集模型结果的提升度进行对比，图 4为非居民及居民客户停电敏感度对比.

由图 4知，在测试集中，非居民及居民客户的验证集累积提升度曲线及敏感客户累积敏感度曲线具有比较接近的变化趋势，这表明决策树CHAID算法模型的普适性较好，在模型中过拟合问题不存在，也就是决策树CHAID算法模型对样本客户具有较好的拟合，但对非选定样本客户的拟合则具有较差的效果.

表 1为测试集客户停电敏感度模型验证结果，据表 1可得，在样本客户中的停电敏感客户的原始纯度依次为居民5.45%，非居民客户8.32%.根据决策树CHAID算法，该模型从高到低计算概率排名，在前5%的住宅客户和非住宅客户中，累积提升度依次为2.50倍、2.52倍.这表明决策树CHAID算法模型试验结果较好.

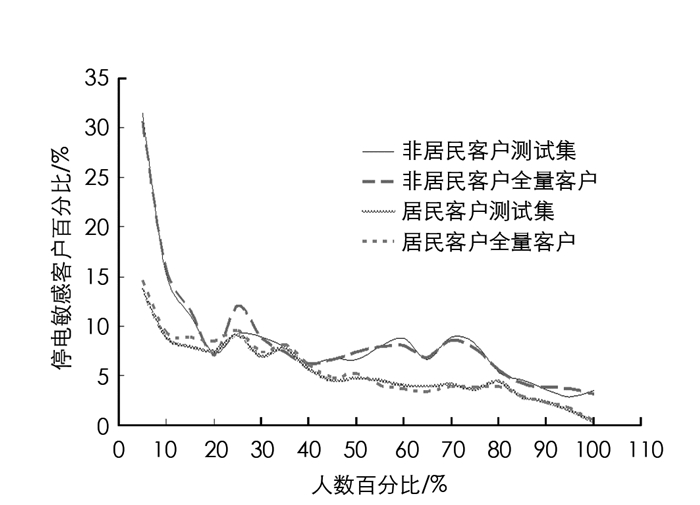
对建模试验结果进行分析，本研究通过决策树CHAID算法模型完成居民客户、非居民客户的停电敏感度建模.将该模型在研究的供电局全体居民客户、非居民客户中进行应用，同时对测试集结果、全量客户结果进行比对，图 5为客户停电敏感度分群结果.

由图 5可知，通过敏感客户百分比从高到低排名可发现，在各占比分段中，对于居民客户、非居民客户来说，全量客户中停电敏感客户占比和测试集停电敏感客户占比比较接近，这表明决策树CHAID算法模型过拟合问题不存在，对于全量客户能很好适用.以此为依据，按照预测的停电敏感度概率，将结果按自高到低的顺序排列，对居民客户和非居民客户分别通过打电话进行咨询，同时对停电相关客户按比例进行查询、识别，结果表明，决策树CHAID算法模型区分程度最高的是全量客户，存在明显的停电敏感客户的实际比例差异是在非居民客户群体和划分出的居民客户间.

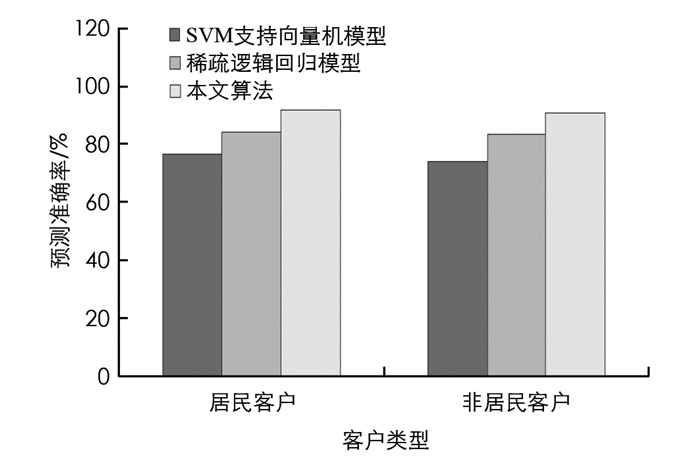
图 6为决策树CHAID算法模型、稀疏逻辑回归模型、SVM支持向量机模型3种算法的预测准确率，在实验中，设置本文算法及稀疏逻辑回归模型的判别阈值为0.70，由图 6知，SVM支持向量机模型要比本文算法及稀疏逻辑回归模型低，在居民客户、非居民客户以及全体客户预测准确率中，本文算法均高于另外两种模型.

本文基于电力客户分群特征，以广东省某市级供电局全体145.2万客户为研究对象，采用决策树方法对停电敏感度预测算法进行了研究，得出结论如下:

1) 在测试集中，非居民及居民客户的验证集累积提升度曲线及敏感客户累积提升度曲线具有比较接近的变化趋势，这表明决策树CHAID算法模型的普适性较好，在模型中过拟合问题不存在.

2) 决策树CHAID算法模型区分程度最高的是全量客户，存在明显的停电敏感客户的实际比例差异是在非居民客户群体和划分出的居民客户间.

3) 通过分析决策树CHAID算法模型、稀疏逻辑回归模型、SVM支持向量机模型3种算法的准确率预测，在居民客户、非居民客户以及全体客户预测准确率中，决策树CHAID算法均高于另外两种模型.