Existence of Positive Solutions for a Class of Second Order Neumann Problem with Sign-Changing Green′s Function

LI Zhao-qian

doi:10.13718/j.cnki.xsxb.2020.12.008

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

In this paper, a class of second-order nonlinear Neumann problems has been studied with sign-changing Green′s function $\left\{ \begin{array}{l} {u^{\prime \prime }} + {m^2}u = \lambda g(t)f(u)\;\;\;\;\;\;t \in [0,1]\\ {u^\prime }(0) = {u^\prime }(1) = 0 \end{array} \right.$ Where \lt i \gt λ \lt /i \gt is a positive parameter, $m \in \left({\frac{\pi }{2}, \frac{\pi }{2} + {\rm{ \mathsf{ ε} }}} \right)$ with \lt i \gt ε \lt /i \gt \gt 0 small, $g:[0, 1] \to { \mathbb{R} _ + }$ is a continuous function, $f:\left[0,\;\infty \right)\to \mathbb{R}$ is a continuous function and \lt i \gt f \lt /i \gt (0) \gt 0 by means of the Schauder fixed point theorem, We obtain the existence of positive solutions.

HTML

非线性二阶常微分方程Neumann问题具有广泛的物理背景，对此类问题的研究已经取得了许多结果^[1-11].但许多学者在研究非线性二阶Neumann问题正解的存在性时，都是在格林函数大于0的情形下研究的^[1-7].特别地，文献[1]在$m \in \left( {0,\;\frac{{\rm{\pi }}}{2}} \right)$的条件下研究了二阶常微分方程Neumann问题

基于锥

运用锥拉伸与压缩不动点定理，得到问题(1)至少存在1个正解，其中非线性项f满足超线性或次线性条件，A，B分别表示问题(1)对应的齐次问题的格林函数的最小值和最大值，且A，B均大于0.

进一步，文献[2]对问题(1)中的非线性项f提出了新的约束条件，运用Leggett-Williams不动点定理，在$m \in \left({0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$的条件下，得到问题(1)至少存在3个非负解，其中f∈C([0, 1]×[0，∞)，[0，∞))且存在常数a，d，使得0 < d < a，且

或

这里$m \in \left({0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$保证了问题(1)的格林函数大于0，但是在格林函数变号的情况下此类问题的研究较少.

注意到：当问题(1)中$m = \frac{{\rm{ \mathsf{ π} }}}{2} + \frac{1}{n} \in \left({\frac{{\rm{ \mathsf{ π} }}}{2}, \frac{{\rm{ \mathsf{ π} }}}{2} + {\rm{ \mathsf{ ε} }}} \right)$，且${G_m}(0, 0) < 0, {G_m}\left({\frac{1}{2}, \frac{1}{2}} \right) > 0$，即问题(1)的格林函数变号.现在的问题是：当格林函数变号时，二阶Neumann问题是否存在正解?基于此，本文将运用Schauder不动点定理考察二阶Neumann问题

正解的存在性，其中λ是正参数，$m \in \left({\frac{{\rm{ \mathsf{ π} }}}{2}, \frac{{\rm{ \mathsf{ π} }}}{2} + {\rm{ \mathsf{ ε} }}} \right), {\rm{ \mathsf{ ε} }} > 0$充分小.

记G_m(t，s)是问题(2)对应的齐次问题

的格林函数，则

令G_m(t，s)=G_m⁺(t，s)－G_m^－(t，s)，其中

本文总假定：

(H1) f：[0，∞)→$\mathbb{R} $为连续函数且f(0)>0；

(H2) g：[0, 1]→$\mathbb{R} $₊连续且在(0，1)的任一子区间内不恒为0；

(H3) 存在常数k>0，使得$\int_0^1 {G_m^ + } (t, s)g(s){\rm{d}}s \ge (1 + k)\int_0^1 {G_m^ - } (t, s)g(s){\rm{d}}s, t \in [0, 1]$.

引理1  问题(2)对应的齐次问题的格林函数G_m(t，s)在(t，s)∈[0, 1]×[0, 1]上有以下性质：

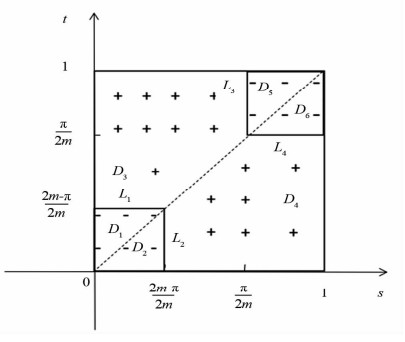
(ⅰ) G_m(t，s)在(t，s)∈[0, 1]×[0, 1]上变号，如图 1所示.在图 1中$m \in \left({\frac{{\rm{ \mathsf{ π} }}}{2}, \frac{{\rm{ \mathsf{ π} }}}{2} + \varepsilon } \right)$，其中ε>0充分小，“+”表示G_m(t，s)>0，“-”表示G_m(t，s) < 0.

当(t，s)属于线段L₁，L₂，L₃，L₄时，G_m(t，s)=0；

当(t，s)属于D₁，D₂，D₅，D₆区域时，G_m(t，s) < 0；

当(t，s)属于D₃，D₄区域时，G_m(t，s)>0.

(ⅱ)∫₀¹G_m(t，s)ds>0.

证   (i)分两种情况进行讨论：

情形1   0≤s≤t≤1.

因为$m \in \left({\frac{{\rm{ \mathsf{ π} }}}{2}, \frac{{\rm{ \mathsf{ π} }}}{2} + {\rm{ \mathsf{ ε} }}} \right)$，其中ε>0充分小，所以msin m>0.因此G_m(t，s)的符号与cos m(1－t)·cos ms的符号一致.

(a) G_m(t，s)=0.

当cos m(1－t)=0或cos ms=0时，G_m(t，s)=0.此时s，t满足$0 \le s \le t = \frac{{2m - {\rm{ \mathsf{ π} }}}}{{2m}}{\rm{ }}$或$\frac{{\rm{ \mathsf{ π} }}}{{2m}} = s \le t \le 1$.即(t，s)属于图 1中的线段L₁或L₃.

当cos m(1－t)=0，cos ms=0时，G_m(t，s)=0.但是s，t不满足s≤t，故舍去.

(b) G_m(t，s) < 0.

当cos m(1－t)>0，cos ms < 0，或cos m(1－t) < 0，cos ms>0时，G_m(t，s) < 0.此时s，t满足$\frac{{2m - {\rm{ \mathsf{ π} }}}}{{2m}} < t \le 1, \frac{{\rm{ \mathsf{ π} }}}{{2m}} < s \le 1$，或$0 \le t = \frac{{2m - {\rm{ \mathsf{ π} }}}}{{2m}}{\rm{, }}\; {\rm{ 0}} \le s < \frac{{\rm{ \mathsf{ π} }}}{{2m}}$.即(t，s)属于图 1中的D₁区域或D₅区域.

(c) G_m(t，s)>0.

当cos m(1－t)>0且cos ms>0时，G_m(t，s)>0.此时s，t满足$\frac{{2m - {\rm{ \mathsf{ π} }}}}{{2m}} < t \le 1$且$0 \leqslant s < \frac{\pi}{2 m}$.即(t，s)属于图 1中的D₃区域.

当cos m(1－t) < 0且cos ms < 0时，G_m(t，s)>0.但是s，t不满足s≤t，故舍去.

情形2   0≤t≤s≤1.

同理可得：

(d) G_m(t，s)=0.

当(t，s)属于图 1中的线段L₂或L₄时，G_m(t，s)=0.

(e) G_m(t，s) < 0.

当(t，s)属于图 1中的D₂区域或D₆区域时，G_m(t，s) < 0.

(f) G_m(t，s)>0.

当(t，s)属于图 1中的D₄区域时，G_m(t，s)>0.

(ii)

引理2^[12]   (Schauder 不动点定理)设D是Banach空间X中的有界闭凸集，A：D→D全连续，则A在D中必有不动点，即存在x^*∈D，使得Ax^*=x^*.

定理1  假设条件(H2)成立，若$\tilde f$：$\mathbb{R} $→$\mathbb{R} $，且存在常数M>0使得|$\tilde f$(s)|≤M，则∀λ∈$\mathbb{R} $，问题

至少存在1个解u_λ∈C[0, 1].

证  令E=C[0, 1]，则E在范数$\left\| u \right\| = \mathop {{\rm{max}}}\limits_{t \in \left[ {0,{\rm{ }}1} \right]} |u(t)|$下构成Banach空间. B是闭凸集，定义为

其中R是待定的正常数.

定义算子F_λ：B→E为

问题(3)有解等价于算子方程F_λu=u有不动点.由于对任意的u∈B，t∈[0, 1]，都有

取R=|λ|Mmax|G_m| ‖g‖，则F_λ(B)⊂B.因为G_m(t，s)在[0, 1]×[0, 1]上连续且g在[0, 1]上连续，因此易证F_λ：B→B是全连续算子.

根据引理2可知F_λ至少存在1个不动点u_λ∈[0, 1].故问题(3)至少存在1个解u_λ∈C[0, 1].

定理2  假设条件(H1)-(H3)成立，则存在λ₀>0，使得当0 < λ < λ₀时，问题(2)至少存在1个正解.

证  固定一个足够大的M，定义函数为h：$\mathbb{R} $→$\mathbb{R} $为

由定理1可知，对任意的λ∈$\mathbb{R} $，问题

至少存在1个解u_λ∈C[0, 1].

固定$\gamma \in \left({0, \frac{k}{{2 + k}}} \right), k > 0$，由h的连续性可知，存在δ∈(0，M)使得

因为

从而存在λ₀>0，使得

因此

因为$\gamma \in \left({0, \frac{k}{{2 + k}}} \right)$，从而(4)式右端非负，因此问题(2)存在解u_λ∈C[0, 1]，t∈[0, 1].

例1  考虑二阶Neumann边值问题

正解的存在性，其中λ是正参数，$m \in \left({\frac{{\rm{ \mathsf{ π} }}}{2}, \frac{{\rm{ \mathsf{ π} }}}{2} + {\rm{ \mathsf{ ε} }}} \right), {\rm{ \mathsf{ ε} }} > 0$充分小.

这里f(u)=u+1，g(t)=1，因此条件(H1)，(H2)成立.由引理1知$\int_0^1 {{G_m}} (t, s){\rm{d}}s > 0$，故存在常数k>0使得条件(H3)成立.

因此由定理2可知，存在λ₀=m²>0，使得当0 < λ < λ₀=m²时，问题(5)有唯一的正解$u = \frac{\lambda }{{{m^2} - \lambda }}$.

Figure (1) Reference (12)

Name
	Name cannot be empty!
E-mail
	Mailbox cannot be empty! Mailbox cannot be empty!
Telephone
	Mobile number cannot be empty! Please enter a valid mobile number!
Title

Content
Verification Code

[1]	JIANG D Q, LIU H Z. Existence of Positive Solutions to Second Order Neumann Boundary Value Problems[J]. Journal of Mathematical Research and Exposition, 2000, 20(3): 360-364. Google Scholar
[2]	SUN J P, LI W T, CHENG S S. Three Positive Solutions for Second-Order Neumann Boundary Value Problems[J]. Applied Mathematics Letters, 2004, 17(9): 1079-1084. Google Scholar
[3]	CHEN X P, LI R G. Existence of Multiple Positive Solutions to Singular Second Order Neumann Boundary Value Problems[J]. Ann Differential Equations, 2010, 26(2): 136-143. Google Scholar
[4]	陈瑞鹏, 马如云, 闫东明.二阶常微分方程Neumann边值问题正解的全局分歧[J].应用数学学报, 2012, 35(3): 515-528. Google Scholar
[5]	ZHANG Y W, LI H X. Positive Solutions of a Second-Order Neumann Boundary Value Problem with a Parameter[J]. Bulletin of the Australian Mathematical Society, 2012, 86(2): 244-253. Google Scholar
[6]	马如云, 陈瑞鹏, 李杰梅.非线性Neumann问题正解的存在性[J].数学学报, 2013, 56(3): 289-300. Google Scholar
[7]	WANG F, ZHANG F. Existence of Positive Solutions of Neumann Boundary Value Problem Via a Cone Compression-Expansion Fixed Point Theorem of Functional Type[J]. Journal of Applied Mathematics Computing, 2011, 35(2): 341-349. Google Scholar
[8]	BOSCAGGIN A, GARRIONE M. Positive Solutions to Indefinite Neumann Problems When the Weight Has Positive Average[J]. Discrete Contin Dyn Syst, 2016, 36(10): 5231-5244. Google Scholar
[9]	CIANCIARUSO F, INFANTE G, PIETRAMALA P. Multiple Positive Radial Solutions for Neumann Elliptic Systems With Gradient Dependence[J]. Math Methods Appl Sci, 2018, 41(16): 6358-6367. Google Scholar
[10]	LEI C Y. Existence and Multiplicity of Positive Solutions for Neumann Problems Involving Singularity and Critical Growth[J]. J Math Anal Appl, 2018, 459(2): 959-979. Google Scholar
[11]	王守财, 赵仕海, 熊宗洪, 等.一类带Neumann边界条件的Kirchhoff型方程解的多重性[J].西南师范大学学报(自然科学版), 2019, 44(4): 11-15. Google Scholar
[12]	郭大钧, 孙经先, 刘兆理.非线性常微分方程泛函方法[M]. 2版.济南:山东科学技术出版社, 2005: 90. Google Scholar

Message Board

Existence of Positive Solutions for a Class of Second Order Neumann Problem with Sign-Changing Green′s Function

Abstract

References

Access History

通讯作者: 陈斌, bchen63@163.com

Article Metrics

Access History

Other Articles By Authors