Right Weak Bruhat Order on Permutations and Quasi-Symmetric Generating Functions

为了讨论方便，我们需要引入一些基本概念和记号.

给定正整数n，如果正整数序列α=(α₁，α₂，…，α_k)满足α₁+α₂+…+α_k=n，则称α为n的一个合成，记为$ \alpha \left| = \right.n $. 我们知道n的所有合成与[n-1]的所有子集之间是一一对应的. 具体而言，给定合成α=(α₁，α₂，…，α_k)|=n，记S_α={α₁，α₁+α₂，…，α₁+α₂+…+α_k-1}是α对应的集合，反之，对于集合S={s₁，s₂，…，s_k-1} _< ⊆[n-1]，它对应的合成为(s₁，s₂-s₁，…，s_k-1-s_k-2，n-s_k-1)，记为α_S. 设α=(α₁，α₂，…，α_k)，β=(β₁，β₂，…，β_l)是n的合成，如果S_β⊆ S_α，则称α是β的细分，记为$ \alpha \preceq \beta $.

给定合成α=(α₁，α₂，…，α_k)|=n，记单项式拟对称函数为M_α，即

由等式(1)可得

基于上述双射$ \alpha \mapsto {{S}_{\alpha }} $，我们既可以用集合也可以用合成作为指标来标记拟对称函数. 事实上，$ {{M}_{S}}\triangleq {{M}_{{{\alpha }_{S}}}}, {{F}_{\alpha }}\triangleq {{F}_{{{S}_{\alpha }}}} $，其中S⊆[n-1]，α|=n. 于是等式(2)等价于

更多拟对称函数相关知识可参见文献[6-7].

给定正整数n，如果正整数序列λ=(λ₁，λ₂，…，λ_k)满足λ₁≥λ₂≥…≥λ_k且λ₁+λ₂+…+λ_k=n，则称λ为n的一个分拆，记为λ├n. 对称函数的各组经典的基(见文献[7])可用整数分拆来标记. 给定λ├n，记m_λ为单项式对称函数，即

其中α取遍λ的所有排列. 对正整数k，令

给定分拆λ=(λ₁，λ₂，…，λ_l)，定义完全齐次对称函数h_λ=h_λ1h_λ2… h_λl及初等对称函数e_λ=e_λ1e_λ2… e_λl.

给定排列$ \pi = {\pi _1}{\pi _2} \cdots {\pi _n} \in {\mathscr{S}_n} $，如果π中不存在i < j < k使得π_i < π_k < π_j，则称π是避免132模式的排列. 令$ {\mathscr{S}_n}\left( {132} \right) $表示$ {\mathscr{S}_n} $中避免132模式的所有排列构成的集合. 类似地，我们也可以定义避免213模式的排列. 令$ {\mathscr{S}_n}\left( {132, 213} \right) $表示$ {\mathscr{S}_n} $中既避免132模式也避免213模式的所有排列构成的集合. 集合$ {\mathscr{S}_n}\left( {231, 312} \right) $也有类似的定义(参见文献[8-9]). 设$ \pi = {\pi _1}{\pi _2} \cdots {\pi _n} \in {\mathscr{S}_n} $，称π^c=(n+1-π₁)(n+1-π₂)…(n+1-π_n)为π的补排列. 显然，$ \pi \in {\mathscr{S}_n}\left( {132, 213} \right) $当且仅当$ {\pi ^c} \in {\mathscr{S}_n}\left( {231, 312} \right) $. 不难验证$ \left| {{\mathscr{S}_n}\left( {132, 213} \right)} \right| = {2^{n - 1}} $，事实上，对$ \pi \in {\mathscr{S}_n}\left( {132, 213} \right) $，有Des(π)⊆[n-1]，反之，对S={s₁，s₂，…，s_k} _< ⊆[n-1]，记s₀=0，s_k+1=n，α=α_S，令

其中·为连接运算，I_α⁽ⁱ⁾表示集合

中元素按递增方式得到的排列. 则显然π_S是$ {\mathscr{S}_n}\left( {132, 213} \right) $中唯一满足条件Des(π_S)=S的排列. 例如，令n=11，S={2，5，7}⊆[10]，则$ {\pi _S} = \begin{array}{*{20}{c}} {10}&{11}&7&8&9&5&6&1&2&3&4 \end{array} \in {\mathscr{S}_n}\left( {132, 213} \right) $.

给定$ \pi = {\pi _1}{\pi _2} \cdots {\pi _n} \in {\mathscr{S}_n} $，称Inv(π)={(π_i，π_j)：1≤i < j≤n，π_i>π_j}为排列π的逆序集. 集合$ {\mathscr{S}_n} $上的右弱Bruhat序≤_R定义如下：π≤_Rσ当且仅当Inv(π)⊆ Inv(σ). 由于$ {\mathscr{S}_n} $中的排列π可以看成如下双射：

则该双射的逆映射也对应一个排列，记为π^-1. 集合$ {\mathscr{S}_n} $上的左弱Bruhat序≤_L定义如下：π≤_Lσ当且仅当π^-1≤_Rσ^-1(见文献[10]). 令

及

分别表示π在右弱Bruhat序下的主理想及对偶主理想.

在证明本文的主要结果时，我们需要用到以下引理：

引理1^[11]  给定S⊆[n-1]，设π_S的定义由等式(3)给出. 则对任意$ \tau \in {\mathscr{S}_n}, {\rm{Des}}\left( \tau \right) \subseteq S $的充要条件是τ≤_Lπ_S.

证  首先证明必要性. 设Des(τ)=T⊆S，令T={t₁，t₂，…，t_k} _< ，t₀=0，t_k+1=n. 由π_T及π_T^-1的定义知

其中·为连接运算，$ \bar I_T^{\left( i \right)} $表示集合

中元素按递增方式得到的排列. 于是

显然Inv(τ^-1)⊆Inv(π_T^-1)，即τ≤_Lπ_T. 由等式(5)易知π_T≤_Lπ_S当且仅当T⊆S. 因此τ≤_Lπ_S.

反之，设τ≤_Lπ_S. 对∀i∈Des(τ)有(τ_i，τ_i+1)∈Inv(τ)，即(i+1，i)∈Inv(τ^-1). 而Inv(τ^-1)⊆Inv(π_S^-1)，于是(i+1，i)∈Inv(π_S^-1)，所以((π_S)_i，(π_S)_i+1)∈Inv(π_S)，即i∈Des(π_S)=S. 因此，Des(τ)⊆ S.

由引理1的证明容易推出以下引理：

引理2  设$ \tau \in {S_n}, \sigma \in {\mathscr{S}_n}\left( {132, 213} \right) $. 则τ≤_Lσ的充要条件是Des(τ)⊆ Des(σ)，即

给定$ \pi \in {\mathscr{S}_n} $，将α_Des(π)中元素按递减方式排列得到的分拆记为λ_π.

定理1的证明  由引理2可得

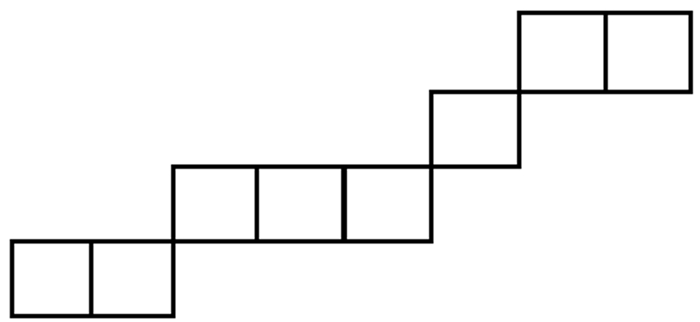
设α=α_Des(π^-1)=(α₁，α₂，…，α_k+1)|=n，记$ {\mathscr{H}_\alpha } $表示大小为n的水平带形，其中第k+2-i行有α_i个方格，例如，当n=8，α=(2，3，1，2)时，它所对应的水平带形如图 1所示.

令$ {\rm{SYT}}\left( {{\mathscr{H}_\alpha }} \right) $表示所有形状为$ {\mathscr{H}_\alpha } $的标准杨表的集合. 根据文献[2]，对$ \forall T \in {\rm{SYT}}\left( {{\mathscr{H}_\alpha }} \right) $，对T从下到上且每行从左到右进行读数可以唯一地得到一个排列τ_T满足Des(τ_T)⊆ Des(π^-1). 显然$ T \longmapsto {{\tau }_{T}} $是一个双射且满足Des(τ_T^-1)=Des(T). 因此

令$ {{s}_{{{\mathscr{H}}_{\alpha }}}} $表示形状为$ {\mathscr{H}_\alpha } $的斜Schur函数，即形式幂级数

其中T取遍所有形状为$ {\mathscr{H}_\alpha } $的半标准杨表(见文献[7]的定义7.10.1). 由文献[7]的定理7.19.7知

容易验证，若$ \pi \in {{\mathscr{S}}_{n}}\left( 132, 213 \right), 则 {{\pi }^{-1}}\in {{\mathscr{S}}_{n}}\left( 132, 213 \right) $且α_Des(π)=(α_k+1，α_k，…，α₁)，故λ_π=λ_π^-1. 因此，由斜Schur函数及完全齐次对称函数的定义可得

上述证明方法主要通过斜Schur函数将$ \mathscr{Q}\left( {{\mathit{\Lambda} }_{\pi }} \right)与 {{h}_{{{\lambda }_{\pi }}}} $联系起来. 下面我们借用单项式拟对称函数与单项式对称函数给出定理1的另一种证明方法.

定理1的另一证明  根据文献[11]，映射$ \tau \longmapsto \text{Des}\left( \tau \right) $可以诱导出从排列上的Hopf代数$ \mathscr{S}Sym $到拟对称函数的Hopf代数$ \mathscr{Q}Sym $之间的一个同态$ \mathscr{D} $如下：

$ \coprod\nolimits_{n\ge 0}{\left\{ {{\mathscr{F}}_{\tau }}:\tau \in {{\mathscr{S}}_{n}} \right\}} $表示$ \mathscr{S}Sym $的基本基. 根据文献[11]中的等式(1.12)可定义$ \mathscr{S}Sym $的单项式基$ \coprod\nolimits_{n\ge 0}{\left\{ {{\mathscr{M}}_{\sigma }}:\sigma \in {{\mathscr{S}}_{n}} \right\}} $为

其中$ {{\mu }_{{{\mathscr{S}}_{n}}}} $(•, •)表示$ {{\mathscr{S}}_{n}} $上左弱Bruhat偏序的莫比乌斯函数. 由莫比乌斯反演公式可得

因此，我们有

由文献[11]的定理7.3知

又由引理2可得

设α=α_Des(π)=(α₁，α₂，…，α_k+1)|=n，因为$ \pi \in {{\mathscr{S}}_{n}}\left( 132, 213 \right) $，则由等式(3)知

对∀β=(β₁，β₂，…，β_l+1)|=n，记

给定两个各项互异的正整数列u=u₁u₂… u_m，v=v₁v₂… v_n，其中{u₁，u₂，…，u_m}∩{v₁，v₂，…，v_n}=Ø. 如果w=w₁w₂… w_m+n是集合{u₁，u₂，…，u_m，v₁，v₂，…，v_n}上的一个排列，且存在1≤i₁ < i₂ < … < i_m≤m+n使得子列w_i1w_i2… w_im=u，w_j1w_j2… w_jn=v，其中{j₁，j₂，…，j_n} _< =[m+n]\{i₁，i₂，…，i_m}，则称w为u和v的一个洗牌，记uШv表示u和v的所有洗牌的集合，见文献[12]. 由≤_R的定义及等式(6)易知τ≤_Rπ当且仅当

令S_β={s₁，s₂，…，s_l}，s₀=0，s_l+1=n. 对任意τ∈X_π，β，记$ \mathscr{J}_{\tau }^{\left( j \right)}=\left\{ {{\tau }_{{{s}_{j-1}}+1}}, {{\tau }_{{{s}_{j-1}}+2}}, \cdots , {{\tau }_{{{s}_{j}}}} \right\}, 1\le j\le l+1 $. 由Des(τ)⊆ S_β可知

其中·为连接运算，$ J_{\tau }^{\left( j \right)} $表示集合$ \mathscr{J}_{\tau }^{\left( j \right)} $中元素按递增方式得到的排列. 令

其中$ \mathscr{I}_{\alpha }^{\left( i \right)} $的定义见等式(4). 于是可以得到矩阵A_τ=(a_i，j)_i，j≥1，容易看出

且

因此矩阵A_τ的行和向量row(A_τ)=α，列和向量col(A_τ)=β. 例如，设$ \pi =789562341\in {{\mathscr{S}}_{9}}\left( 132, 213 \right), \beta =\left( 2, 4, 3 \right)\left| = \right.9 $. 于是α=α_Des(π)=(3，2，3，1)，S_β={2，6}. 对τ=275689134∈X_π，β，有

且满足行和向量row(A_τ)=(3，2，3，1)=α，列和向量col(A_τ)=(2，4，3)=β.

记

易知$ \tau \longmapsto {{\boldsymbol{A}}_{\tau }} $是X_π，β到Y_α，β的双射. 于是

从而由文献[7]的命题7.5.1知$ \mathscr{Q}\left( {{\mathit{\Lambda} }_{\pi }} \right)={{h}_{{{\lambda }_{\pi }}}} $.

定理2的证明  设α=α_Des(π^c)=(α₁，α₂，…，α_k+1). 首先由条件知$ {{\pi }^{c}}\in {{\mathscr{S}}_{n}}\left( 132, 213 \right) $，因此由等式(3)易知π=π^-1. 此外，不难验证：对$ \forall \sigma , \tau \in {{\mathscr{S}}_{n}}, \sigma {{\le }_{L}}\tau $当且仅当τ^c≤_Lσ^c. 基于这两个事实，接下来的证明过程与定理1的第一种证明方法类似，只需将其中的水平带形改为大小为n的垂直带形$ {{\mathscr{V}}_{\alpha }} $，则可推出

再由斜Schur函数和初等对称函数的定义得，$ {{s}_{{{\mathscr{V}}_{\alpha }}}}={{e}_{{{\lambda }_{{{\pi }^{c}}}}}} $，从而定理2得证.

类似于定理1的第二种证明方法，我们可以给出定理2的另一证明. 证明过程主要应用以下两个等式：

其中等式(7)由文献[11]的定理7.3和引理2推出，等式(8)由文献[7]的命题7.4.1得出.

本文分别给出了拟对称生成函数$ \mathscr{Q}\left( {{\Lambda }_{\pi }} \right)\And \mathscr{Q}\left( {{V}_{\pi }} \right) $)是对称函数的一个充分条件，通过计算机编程计算，我们发现当n≤8时，该充分条件也是必要条件，但尚未找到合适的证明方法. 因此，在本文最后，我们提出下列猜想：

猜想1  设$ \pi \in {{\mathscr{S}}_{n}}, 则 \mathscr{Q}\left( {{\Lambda }_{\pi }} \right) $是对称函数的充要条件是$ \pi \in {{\mathscr{S}}_{n}}\left( 132, 213 \right) $.

猜想2  设$ \pi \in {{\mathscr{S}}_{n}}, 则 \mathscr{Q}\left( {{V}_{\pi }} \right) $是对称函数的充要条件是$ \pi \in {{\mathscr{S}}_{n}}\left( 231, 312 \right) $.