On the Law of Atomic Vibration of Sensor Porous Electrode Material with Temperature

传感器Pt电极材料中有许多小孔, 不同烧结温度下多孔Pt电极的SEM图^[1]见图 1a. 从图 1可看出, 多孔Pt电极可看作许多颗粒彼此靠近而成. 各颗粒大小、形状差别不大, 在研究线膨胀等热学性质时, 作为简单考虑, 可把多孔Pt电极材料视为由半径相同的许多硬球型Pt晶粒堆积而成, 晶粒在0.1~10 μm之间变化(图 1b).

Pt电极的特点是多孔性, 孔隙的程度不仅直接影响渗透到电极处参加电解反应的气体的多少, 而且也影响Pt电极材料的性能. 设电极材料体积为V, Pt晶粒总体积V₀, 则孔隙体积(V-V₀)与材料体积V之比称为材料的孔隙度(ζ), 即: ζ=1-V₀/V. 设单位体积Pt电极材料内的Pt晶粒有n₀颗, 晶粒平均半径为R, 则电极材料的孔隙度ζ与R的关系为

Pt电极的多孔性导致它的第2个特点, 即表面效应显著. 按照表面物理理论, 表面层的原子, 由于原子周围情况与体内不同, 表面原子的配位数比体内少, 使表面原子失去体内原子那样原子排列的对称性, 因而表面层的原子相互作用与内部不同. 研究表明, 离表面3个晶格常数a的厚度范围为表面层^[6]. 对Pt电极, 晶粒小(平均粒径0.1~10 μm), 表面层的原子数占总原子数比率大. 为了描述表面效应的大小, 将表面层的原子数N′与总原子数N的比值$\eta = \frac{{N'}}{N}$称为表面层参数. 可求得表面层参数η与晶粒半径的关系为

由(1)式和(2)式求得孔隙度(ζ)与表面层参数η的关系为

由(1)-(3)式看出, 孔隙度愈大, 晶粒平均半径R愈小, 表面层参数η愈大, 表面效应愈大. 多孔Pt电极的第3个特点是其长期处于高温可变的工作环境中, 原子振动的非简谐效应显著. 为了描述非简谐效应的大小, 将一个原子平均相互作用能为φ(r)在平衡位置r₀附近展开, 偏离ξ=r-r₀很小时, 有

其中, ε₀, ε₁, ε₂分别是简谐系数和第一、第二非简谐系数. 非简谐系数ε₁和ε₂的大小, 反映了原子振动非简谐效应的大小, 其数值取决于材料的具体结构和原子相互作用势.

Pt电极材料为面心立方结构, 按照文献[7], 对Pt这类过渡金属两原子相互作用势可写为

其中, λ_D为平均德拜波长, 与晶格常数a关系为λ_D=4(πF_c/6)a, F_c为结构因子, 对面心立方的晶体, F_c=1/4；g为与成键相关的量；n为键强参数, r₀为平衡时最近的两原子间的距离.

为了求出ε₀, ε₁和ε₂, 由(5)式并结合Pt的具体结构, 以某原子的位置为参考点O, 最近的原子距离为r, 在计及最近邻、次近邻、再次近邻情况下, 求得一个原子平均相互作用能, 进而求得原子振动的简谐系数ε₀与第一和第二非简谐系数ε₁和ε₂, 结果是:

对于表面, 由于表面原子的相互作用势能曲线的不对称性大于体内, 热振动造成的平均位移将大于体内的平均位移. 理论和实验均证明^[8]: 表面原子振动的简谐系数ε′₀、第一和第二非简谐系数ε′₁和ε′₂与体内的简谐系数ε₀、第一和第二非简谐系数ε₁和ε₂的关系为:

简谐近似下, 质量为M的原子的运动为振幅A₀和频率均为常数的简谐运动, 原子平均位移ξ=0. 实际原子作的是非简谐运动, 不仅原子振动频率不为常数, 而且振动产生大量的声子, 声子之间以及声子与材料存在的缺陷(界面、杂质、空位等)之间有相互作用, 必有能量损失. 能量损失不太大时, 能量损失使原子的运动由简谐振动变为阻尼运动, 设阻尼系数为β, 则由阻尼振动方程, 求得解为: ξ=A₀exp(-βt)·cos(ω′t+φ₀), 振幅已由简谐情况的A₀变为A₀exp(-βt), 频率由ω变为ω′. 令κ=(ω-ω′)/ω, 称为阻尼对原子振动频率的影响参量. 在小阻尼情况下, κ很小, 具体数值可由它得到结果与实验比较确定, 也可以通过具体材料的物理量随时间的衰减情况估计. 按哈根穆勒^[9]的看法, 考虑声子之间以及声子与材料存在的缺陷之间有相互作用, 即使在晶体中加入掺杂质原子, 会改变与晶体原子间的相互作用, 但考虑声子之间以及声子与缺陷间相互作用, 或者加入掺杂质原子后的晶体原子间的相互作用, 与未加入前晶体原子间相互作用接近, 晶体才能成稳定结构, 因而κ很小.

为了确定阻尼系数与温度的关系, 设所受的阻尼与原子振动速度成正比, 即$ - \gamma \dot \zeta $, γ与阻尼系数的关系为$\beta = \frac{\gamma }{{2M}}$. 由原子单位长度位移时阻力做功$\gamma \dot \zeta $等于原子能量的减小, 即$\gamma \dot \zeta $=ΔE=ħω-ħω′, 其中的$\dot \zeta $由原子振动的平均动能E_k与平均势能V相等求得: $\dot \zeta $=(ħω/M)^1/2. 于是: γ=κ(Mħω)^1/2. 阻尼系数β=γ/2M随温度的变化为

这里ω₀=(ε₀/M)^1/2是T=0 K时体内原子的振动频率.

当只考虑非简谐效应对频率的影响而不考虑能量损失时, 体内原子振动频率与温度T的关系为^[10]

考虑能量损失后体内原子振动频率与温度T的关系为ω′=(1-κ)ω(T).

同样, 对表面层, 原子振动频率ω′_s和阻尼系数β′随温度的变化为:

ω₀^′=(ε₀^′/M)^1/2是T=0 K时表面层原子的振动频率.

将(4)式代入玻尔兹曼统计求平均值的公式, 可求得原子振动的平均位移. 当只考虑非简谐效应对频率的影响而不考虑能量损失时, 由玻尔兹曼统计求得平均位移与温度T的关系为^[9]

考虑非简谐效应对振幅的影响以及声子之间、声子与缺陷之间相互作用后, 能量损失造成振幅随时间增长而减小, 由简谐情况的A₀变为A₀e^-βt, 由于位移与振幅成正比, 因此, 考虑非简谐效应引起的能量损失后, 体内原子的平均位移就不仅与温度有关, 而且还与时间有关:

类似地, 对表面层有

考虑到体内和表面层原子振动情况的差异, 即平均位移为: ξ (T, t)=(1-η)ξ(T, t)+ηξ′ (T, t), 得到原子平均位移随温度和时间以及颗粒半径R的变化为

将(1)式代入(13)式, 得到原子平均位移随孔隙度ζ的变化为

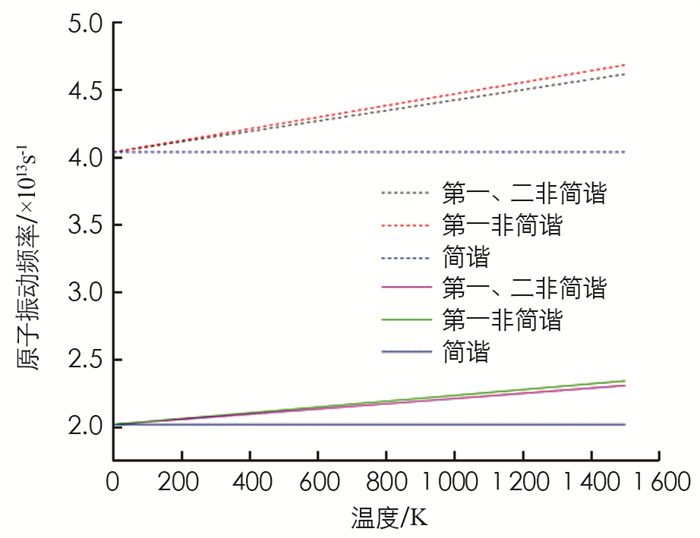
现以多孔Pt电极为例来研究.Pt为面心立方结构, 晶格常数取^[11]a=3.92×10^-10m, 平衡位置时两原子间距离r₀=2.77×10^-26m. 将F_c=1/4, λ_D=2.051×10^-10m, g=7.839×10^-6 eV/cm²和n=9.31等代入(6)式, 求得体内原子振动的简谐系数以及非简谐系数为: ε₀=5.286×10² J/m², ε₁=-12.338×10¹²J/m³, ε₂=11.422×10²²J/m⁴. 由(7)式, 求得表面原子振动的简谐系数以及非简谐系数ε′₀=1.321×10²J/m², ε′₁=-1.542×10¹²J/m³, ε′₂=0.714×10²²J/m⁴. Pt原子质量M=3.238×10^-25kg, 由ω₀=(ε₀/M)^1/2求得ω₀=4.040×10¹³s^-1, 代入(8)-(10)式, 求得Pt电极颗粒表面和体内原子振动频率随温度的变化, 结果见图 2, 图 2中曲线分别是简谐、考虑到第一非简谐、同时考虑到第一和第二非简谐的结果.

由图 2看出, ①体内原子的振动频率始终大于表面原子的振动频率；②在简谐近似下, 原子振动频率为常量(体内为4.040×10¹³s^-1；表面为2.020×10¹³s^-1)；③考虑非简谐效应后, 在0~1 500 K温度变化范围内, 体内与表面原子的振动频率随温度升高而线性增大, 例如温度从T=300 K升温到1 300 K时, 体内与表面原子振动频率分别平均增加了9.806%和9.805%；故温度愈高, 体内与表面原子振动频率逐渐增大, 与简谐近似的差值愈大, 即非简谐效应愈显著.

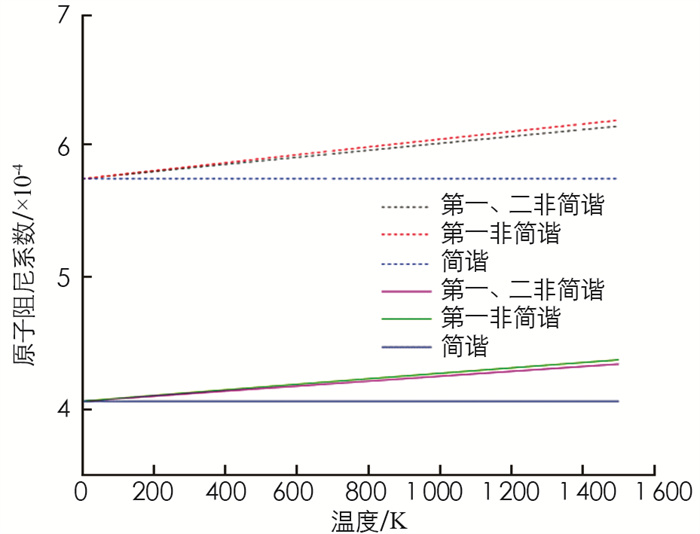
由非简谐效应可设Pt电极中阻尼对原子振动频率的影响参量κ=10^-5, 代入(9)和(10)式, 得到阻尼系数随温度的变化β(T), 结果见图 3.

由图 3可看出, ①在0~1 500 K温度变化范围内颗粒体内的阻尼系数始终大于表面, 且是表面的1.414倍；②在简谐近似下, Pt电极颗粒体内和表面的阻尼系数为常量(体内为5.74×10^-4；表面为4.06×10^-4)；③考虑非简谐效应后, 阻尼系数随温度升高而线性增大, 例如温度从T=300 K升温到1 300 K时, 电极颗粒体内与表面的原子阻尼系数平均分别增加了4.788 1%和4.787 8%；故温度愈高, 电极颗粒的阻尼系数愈大, 且与简谐近似下的差值愈大.

Pt电极阻尼系数随温度升高而增大的原因是: 由于温度升高, 原子振动的非简谐效应越显著, 声子与声子之间的非弹性碰撞加剧, 能量损失增加, 使得振动振幅、振动频率减小, 故阻尼系数越大.

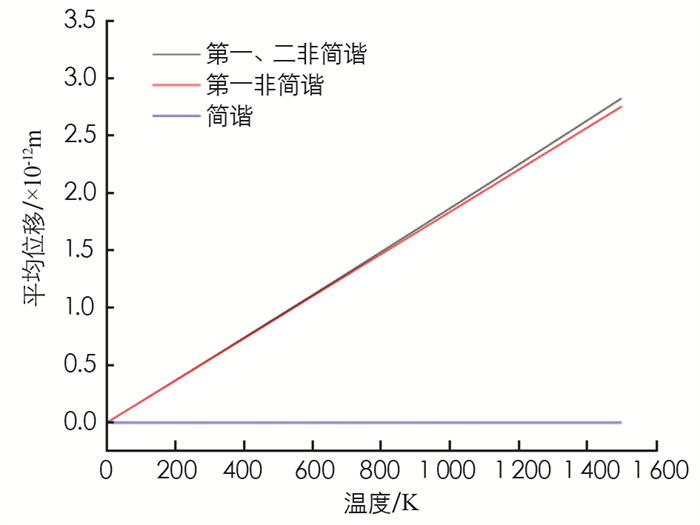
将求出的阻尼系数和体内原子振动的ε₀, ε₁, ε₂以及表面层原子振动的ε′₀, ε′₁, ε′₂, 代入(11), (12)和(13)式, 得到给定时间t=0 s、颗粒平均半径R=10 nm时, Pt电极材料原子平均位移随温度的变化关系, 结果见图 4. 图 4中的实线分别表示考虑到第二非简谐项、第一非简谐项和简谐近似下的结果.

由图 4看出, ①在简谐近似下, 原子平均位移不随温度而变；②考虑非简谐效应后, Pt电极材料的原子平均位移随温度升高而非线性增大, 例如温度从T=300 K升温到1 300 K时, 原子平均位移平均变化了337.080%, 故温度越高, 原子平均位移与简谐近似下的差值愈大.

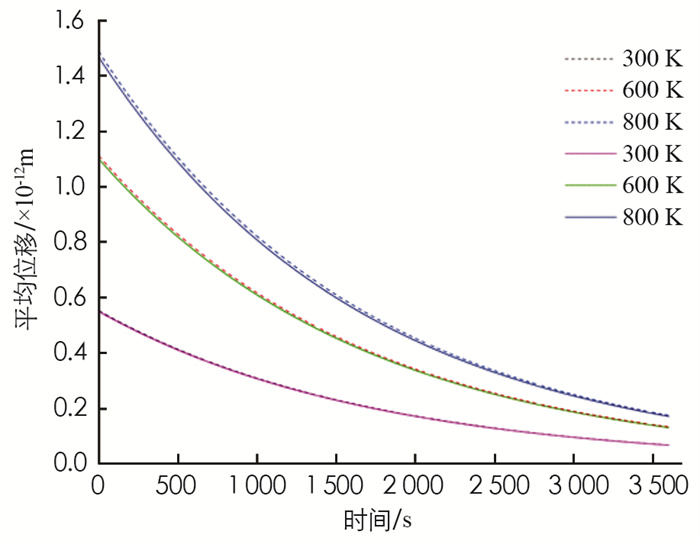
由(13)式, 得到给定温度T=300, 600和800 K, 颗粒平均半径R=10 nm时, 电极材料原子的平均位移随时间的变化关系(图 5), 图 5中曲线表示不同温度下平均位移随时间的变化关系, 虚线表示考虑到第一非简谐项的结果, 实线表示考虑到第二非简谐项的结果.

由图 5看出, ①在简谐近似下, 原子平均位移不随时间而变, ②考虑非简谐效应后, 在时间变化范围为0~3 600 s时, Pt电极材料原子的平均位移随时间的增长而按照负指数规律非线性减小, 例如, 在时间从t=500 s增加到3 000 s时, 平均位移分别减小了76.605%(300 K), 77.096%(600 K)和77.413%(800 K), 且实、虚曲线基本重合, 说明考虑第二非简谐项与第一非简谐项的差距不大, 故时间越短, 非简谐效应愈显著.

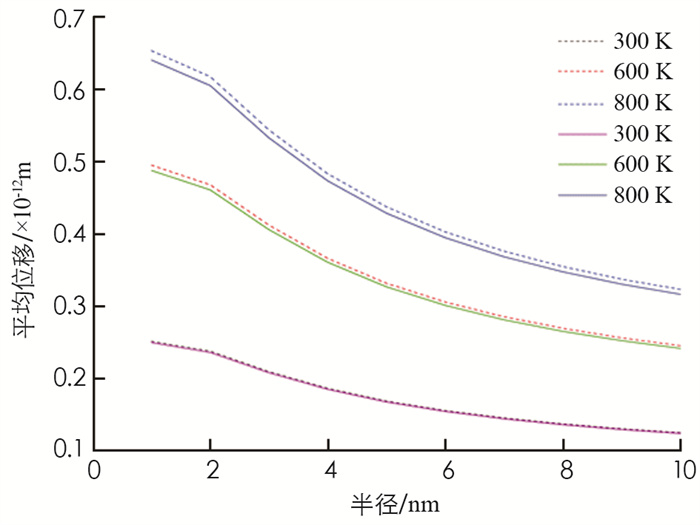
由(13)式, 得到时间取t=3 600 s时, 温度T=300, 600和800 K时, 电极材料原子的平均位移随颗粒平均半径的变化见图 6.

由图 6看出, ①在半径变化范围1~10 nm内, 平均位移随着平均半径的增大而出现明显的非线性减小, 而简谐近似下原子平均位移不随半径而变；②考虑到非简谐效应时, 在半径从3 nm变化到9 nm时, 平均位移分别减小了37.716%(300 K), 37.866%(600 K)和37.964%(800 K), 所以线度愈小, 平均位移愈大, 非简谐效应愈显著.

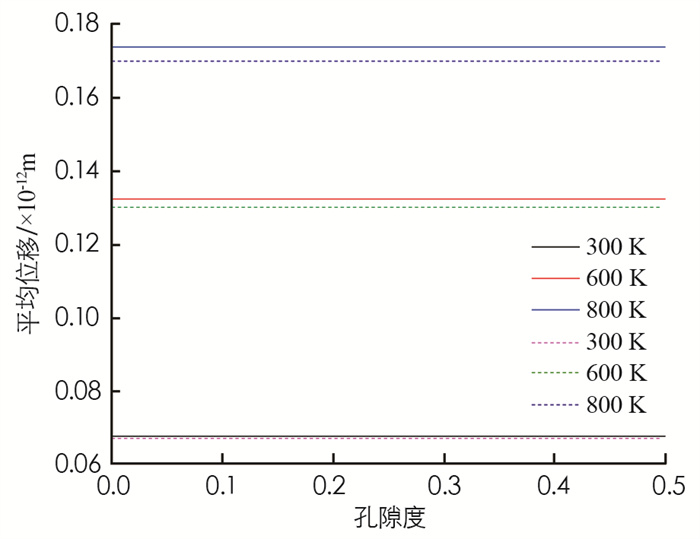
由(14)式, 得到给定时间t=3 600 s时, 温度T=300, 600和800 K时, Pt电极材料平均位移随孔隙度的变化见图 7.

由图 7看出, Pt电极热膨胀系数随孔隙度的增大而增大, 但幅度极小；考虑到非简谐效应, 孔隙度从0.1变化到0.5, 其Pt电极热膨胀系数平均分别增加了1.859×10^-4%(300 K), 1.882×10^-4%(600 K), 1.897×10^-4%(800 K)；故孔隙度愈大, 非简谐与简谐近似下的差距愈大, 即非简谐效应愈显著.

本研究考虑到原子非简谐振动, 探讨了多孔Pt电极材料原子振动频率、阻尼系数随温度的变化特点. 在此基础上, 应用固体物理理论和方法, 对电极材料的热膨胀性能随温度、时间、颗粒线度和孔隙度等的变化规律进行研究, 结果表明: ①原子振动频率随温度升高而线性增大, 表面原子的振动频率总小于体内. 原子振动的振幅受到的阻尼系数均随温度升高而增大, 但体内与表面受的阻尼不同: 体内阻尼系数大于表面, 是表面的1.414倍. ②Pt电极材料原子平均位移随温度升高而非线性增大；随时间的增长而按负指数规律非线性减小, 衰减的情况与温度有关: 温度愈高, 衰减愈大；随颗粒平均半径的增大而非线性减小, 线度愈小, 原子平均位移愈大；随孔隙度的增加而非线性增大, 但幅度极小, 孔隙度从0.1到0.5时, 原子平均位移仅变化了1.859×10^-4%(300 K), 1.882×10^-4%(600 K), 1.897×10^-4%(800 K). ③原子非简谐振动对Pt电极材料原子平均位移有重要影响: 简谐近似下无热膨胀, 原子振动频率、振幅、阻尼系数均为常数. 考虑到非简谐效应后, 原子振动频率、阻尼系数随温度升高而增大, 且与简谐近似的差值愈大；温度越高、平均半径越小, 时间越短, 孔隙度越大, 非简谐效应下原子平均位移与简谐近似下的差值愈大, 即非简谐效应愈明显.