-
小波分析自从出现之日开始,便因为其理论上的优美性和计算上的便利性得到了广泛关注,并最终成为数字信号处理与数字图像处理的标准工具. 构造小波的一个自然而有效的方法是多尺度分析[1]. 基于这一方法,研究者们发现了许多小波,比如Daubechies小波、B-样条小波等. 在众多小波中,B-样条小波因为其在消失矩、对称性、紧支撑性和光滑性等方面的良好性质受到了广泛关注[2]. 尽管小波在许多方面的应用表现优越,但它仍然有一些缺陷,比如对平移的敏感性,在数字图像处理中方向的弱选择性以及缺乏相位信息等. 而数字图像处理已经广泛地融入到生活的各方面,例如医学图像处理[3]、人脸识别[4]、病虫害预测[5]等,因此,许多研究人员试图提出一些改进的方法来解决这些缺陷. 比如文献[6]利用正交小波对来设计可调的滤波器,使之在图像处理中自适应控制相位信息和方向性. 文献[7-10]使用了双树小波滤波器来获得复小波系数的实部和虚部,并成功地用之于数字图像处理. 其后,文献[11-12]发现文献[7-10]构造的双树小波形成了一个近似的希尔伯特变换对,基于这一发现,研究了近似构成希尔伯特变换对的二进小波基的设计过程. 从那以后,小波的希尔伯特变换引起了越来越多的研究人员的关注.
文献[13]基于B-样条分解定理提出了一种巧妙的方法构造小波的希尔伯特变换对. 文献[14]研究了构成希尔伯特变换对的两个小波对应的尺度函数需要满足的相位条件. 进而,文献[15]研究了双正交小波基的希尔伯特变换对的构造. 既然小波的希尔伯特变换如此重要,那么,相对于小波本身,小波的希尔伯特变换是否在光滑性、衰减性、对称性和消失矩等方面也具有良好的性质?它们的表现是否不同于小波本身?小波对应的尺度函数的希尔伯特变换的表现如何?文献[16]试图解决这些问题,并证明了:在一定的光滑性和衰减性条件下,如果小波ψ具有n阶消失矩,那么小波的希尔伯特变换Hψ具有n+1阶的衰减性,并具有n阶消失矩,这一结论是对一般的小波给出的. 鉴于B-样条小波的优良性质,我们好奇B-样条小波的希尔伯特变换是否具有更特殊的性质. 考虑到消失矩在小波中的应用尤其重要,本文重点研究3阶B-样条小波的希尔伯特变换的消失矩性质.
HTML
-
在本节中,我们将介绍一些必要的记号和预备知识. 尽管希尔伯特变换可以定义在一般的Lp(1≤p≤∞) 空间中,本文主要讨论平方可积函数空间L2(
$ {\mathbb{R}} $ )上的希尔伯特变换. 即记f的二范数为而L2(
$ {\mathbb{R}} $ )={f:‖f‖2 < ∞}. 对∀f∈L2($ {\mathbb{R}} $ ),f的希尔伯特变换在x∈$ {\mathbb{R}} $ 处定义为其中p.v.表示柯西主值. 同时注意到
可类似地定义
沿用文献[13]的记号,有‖f‖1,∞=‖f‖1+‖f′‖∞.
如果ψ的二进伸缩和平移
$ \left\{2^{\frac{j}{2}} \psi\left(2^{j} x-k\right): j, k \in \mathbb{Z}\right\} $ 构成了L2($ {\mathbb{R}} $ )的一族规范正交基,则我们称函数ψ是一个小波[16]. 有时候,我们亦会减弱其正交性为双正交性,本文主要讨论的B-样条小波即为一种双正交小波.如果对任意整数0≤k < n,有
$ \int_{\mathbb{R}} x^{k} f(x) \mathrm{d} x=0 \text { 但 } \int_{\mathbb{R}} x^{n} f(x) \mathrm{d} x \neq 0 $ ,则称函数f具有n阶(n≥1)消失矩[17]. 消失矩在小波的诸多性质中占据非常重要的位置. 事实上,由于它如此重要,一些作者甚至将它写入了小波的定义,比如文献[16]定义了一个r阶小波:假设r∈$ {\mathbb{N}} $ ,一个r阶小波是指任意复值函数ψ:$ {\mathbb{R}} $ →$ {\mathbb{C}} $ ,使得ψ及其直到r阶的导数都属于L∞($ {\mathbb{R}} $ ),且满足如下两个条件:(ⅰ) ψ及其直到r阶导数快速衰减;
(ⅱ)对0≤q≤r,有
$ \int_{\mathbb{R}} x^{q} \psi(x) \mathrm{d} x=0 $ .
-
B-样条小波有两种常见的表达方式[18]. 第一种是利用等距节点且相邻节点之间距离为1的基数B-样条函数,将m阶等距节点的基数B-样条函数用Nm表示,则m阶B-样条构造小波ψm可表示为:ψm(x)=
$ \sum_\limits{n} q_{n} N_{m}(2 x-n) $ ,其中系数另一种表达方式是利用特征函数的累次积分,即
其中Pm(4m-3)可由递推关系
得到. 这里的4m-3表示从0开始算起,Pm能取到的最后一个分量数,即Pm的实际长度为4m-2. 这里的L(n,j)和R(n,j-1)为待选定的分段函数. 我们选取和文献[15]一样的L(n,j)和R(n,j-1),即
当m=3时可计算得到P3(9)={1 31 206 626 1 056 1 056 626 206 31 1}. 根据(2)式的定义,我们得到3阶B-样条小波的表达式为
由(3)式及P3(9)可以计算得到
由(4)式可见,3阶B-样条小波ψ3是一个紧支撑的分片多项式,支撑在10个区间长度为0.5的子区间上,在每个子区间内的表达式都是二次函数. 用ψ3,k(x)表示ψ3在第k个区间上的表达式,即ψ3,k(x)=a3(k)x2+b3(k)x+c3(k)(k=1,2,…,10). 利用这一分段多项式的表达式,我们可以确认一个已知的事实:3阶B-样条小波具有3阶消失矩[19].
-
在本节中,我们将基于3阶B-样条小波的分片多项式形式来给出其希尔伯特变换的表达式. 进一步计算3阶B-样条小波的希尔伯特变换的消失矩. 结果表明,3阶B-样条小波的希尔伯特变换比3阶B-样条小波具有更高的消失矩.
-
由希尔伯特变换的定义可知,3阶B-样条小波的希尔伯特变换为
将ψ3的表达式代入,有
接下来探讨(5)式中的积分部分.
将(6)式代入(5)式,得
根据计算发现
$ \sum\limits_{k=1}^{10} a_{3}(k)=0, \sum\limits_{k=1}^{10} b_{3}(k)=0 $ 且$ \sum\limits_{k=1}^{10} k a_{3}(k)=0 $ ,则3阶B-样条小波的希尔伯特变换为为统一性起见,定义ψ3,0(x)=ψ3,11(x)=0. 经过简单的计算发现,3阶B-样条小波的第k+1段与第k段之间有以下关系:
其中
因此得到3阶B-样条小波的希尔伯特变换表达式为
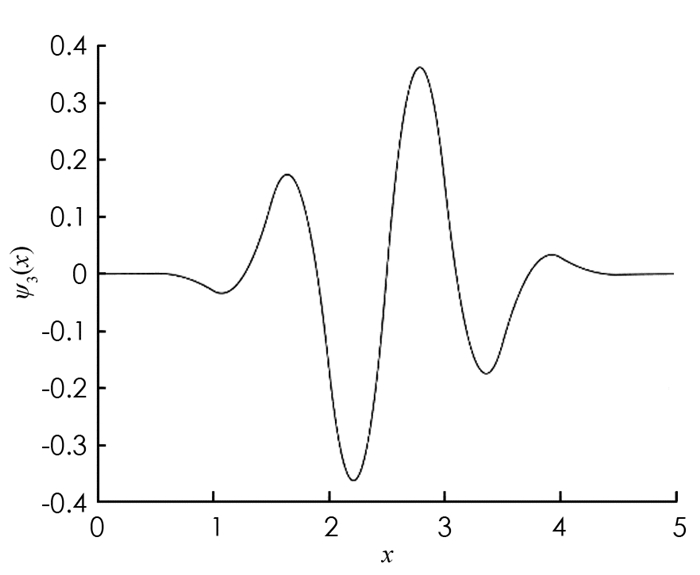
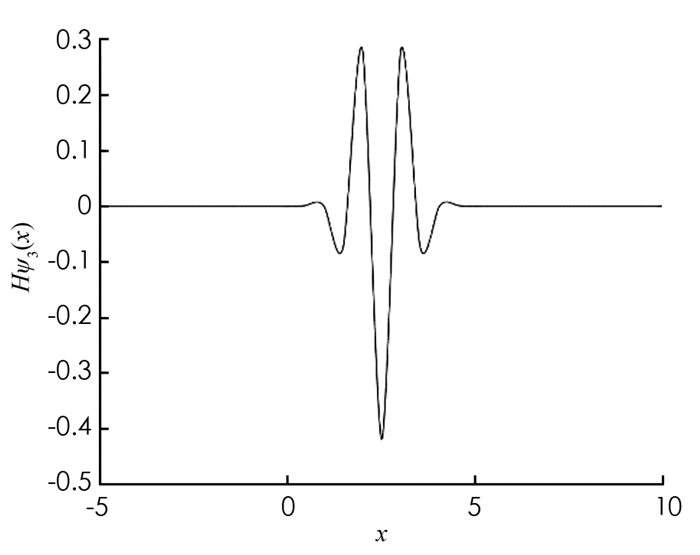
在图 1和图 2中,我们分别给出了3阶B-样条小波和3阶B-样条小波的希尔伯特变换的图像. 可以看到,它们具有可比较的光滑性和对称性,3阶B-样条小波关于其对称中心是反对称的,而它的希尔伯特变换关于其对称中心是对称的. 另外,我们知道,一个紧支撑的函数的希尔伯特变换不再具有有限支撑,因此在下一小节重点关注3阶B-样条小波的希尔伯特变换的消失矩性质.
-
将(7)式代入消失矩的定义,得
对(8)式第三行的积分进行积分变量替换,令
$ t=\frac{k}{2}-x $ ,我们有对(8)式第四行的积分进行积分变量替换,令
$ t=-\frac{k}{2}-x $ ,我们有将(9),(10)式代入(8)式,得
当r是偶数时,根据二项式展开容易得到
所以(11)式变为
其中矩阵K定义为K(i+1,k+1)=ki(i=0,1,…;k=0,1,…,10),h3是一个列向量,它的第k+1分量为
$ \boldsymbol{h}_{3}(k+1)=\frac{(-1)^{k}}{240}\left(Q_{3}\right)_{k} $ . 经计算,Kh3=[0 0 0 0 0 0 48 1 680 …]T,注意到这个向量从第7项开始才不为0,而后面的积分为一个多项式与对数函数乘积的积分,总不等于0. 因此,当i-r+1≥7时VHψ3(i)≠0. 注意到r从0开始计数,可以得到Hψ3(x)有6阶消失矩.文献[13]证明了一个重要的定理,指出若一个可微的小波ψ有n阶消失矩,同时假设‖ψ‖1,∞,‖xn+1ψ(x)‖1,∞以及‖xnψ(x)‖1都有限,则Hψ(x)也有n阶消失矩,且满足
从本文的结果来看,3阶B-样条小波ψ3满足了此定理的所有条件,不过由于3阶B-样条小波本身的特性,它的希尔伯特变换具有6阶消失矩. 为什么会有这一现象发生是我们正进一步思考的问题.
3.1. 3阶B-样条小波希尔伯特变换的表达式
3.2. 3阶B-样条小波希尔伯特变换的消失矩
-
本文首先给出了一个具体的3阶B-样条小波的分片多项式表达形式,然后得到了3阶B-样条小波的希尔伯特变换的一个简洁的表达式,最后计算了3阶B-样条小波的希尔伯特变换的消失矩. 从图像上可以看到,3阶B-样条小波的希尔伯特变换具有和3阶B-样条小波类似的光滑性,同时将3阶B-样条小波的反对称性变为了对称性. 由于紧支撑函数的希尔伯特变换不可能具有有限支撑,我们知道3阶B-样条小波经过希尔伯特变换后付出的代价是衰减性降低了,但从本文的结果可以看到,这一代价的收益便是它具有了更高的消失矩. 这一发现对构成希尔伯特变换对的小波的构造具有启发意义.






 DownLoad:
DownLoad: