The Randić Index in Random Pentagonal Chains and Random Spiro Pentagonal Chains

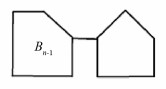
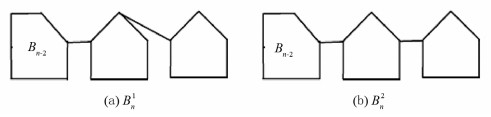
定义1^[4]  由n个五边形构成的α-五角链B_n可视为把由n-1个五边形构成的α-五角链B_n-1和一个五边形通过一条边相连所得(如图 1). 当n≥3时，B_n中最后一个五边形有两种连接方式，分别记为B_n¹与B_n²(如图 2). 因从B_k-1到B_k (k=3，4，…，n)是随机的，故将在α-五角链末端通过逐步增加五边形所得的五角链称为α-随机五角链.

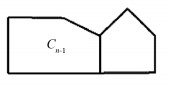
定义2^[4]  由n个五边形构成的β-五角链C_n可视为把由n-1个五边形构成的β-五角链C_n-1和一个五边形用一条共用边相连所得(如图 3). 当n≥3时，C_n中最后一个五边形有两种连接方式，分别记为C_n¹与C_n²(如图 4). 因从C_k-1到C_k (k=3，4，…，n)是随机的，故将在β-五角链末端通过逐步增加五边形所得的五角链称为β-随机五角链.

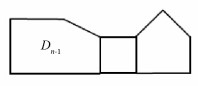
定义3^[4]  由n个五边形构成的γ-五角链D_n可视为把由n-1个五边形构成的γ-五角链D_n-1和一个五边形通过两条边相连所得(如图 5). 当n≥3时，D_n中最后一个五边形有两种连接方式，分别记为D_n¹，D_n²(如图 6). 因从D_k-1到D_k (k=3，4，…，n)是随机的，故将在γ-五角链末端通过逐步增加五边形所得的五角链称为γ-随机五角链.

设从B_n-1(C_n-1；D_n-1)到B_n¹(C_n¹；D_n¹)的概率为p(p₁；p₂)，则从B_n-1(C_n-1；D_n-1)到B_n²(C_n²；D_n²)的概率为1-p(1-p₁；1-p₂). 令R_n^(α)(p)(R_n^(β)(p₁)，R_n^(γ)(p₂))分别表示由n个五边形构成且从B_n-1(C_n-1；D_n-1)到B_n¹(C_n¹；D_n¹)的概率为p(p₁；p₂)的α-(β-，γ-)随机五角链. 注意到R(R_n^(α)(p))，R(R_n^(β)(p₁))及R(R_n^(γ)(p₂))均为随机变量，记它们的期望值分别为

接下来考虑t-随机五角链的Randić 指标的期望，t∈{α，β，γ}.

显然，α-五角链的边只可能是(2，2)，(2，3)，(3，3). 于是由Randić 指标的定义可得

故α-五角链的Randić 指标取决于m_2，2(B_n)，m_2，3(B_n)和m_3，3(B_n)的值.

定理1  设R_n^(α)(p)是一个n长的α-随机五角链，其中n≥2，则

证  当n=2时，直接计算得

当n>2时，显然m_2，2(B_n)，m_2，3(B_n)，m_3，3(B_n)的值由图 2中的两种结构确定.

情形1  设B_n-1到B_n¹的概率为p，则

由(1)式得

情形2  设B_n-1到B_n²的概率为1-p，则

由(1)式得

结合(2)，(3)式得

又因E[E_n^α]=E_n^α，应用期望算子可得

注意到(4)式为一阶常系数非齐次差分方程，显然其所对应的齐次方程的通解为E^α=C，这里C为常数. 设E^α′=kn为(4)式的一个特解，将其代入(4)式可得

故(4)式的通解为

结合初始条件E[R(B₂)]=$\frac{2 \sqrt{6}}{3}+\frac{10}{3}$可得

因此，当n≥2时，有

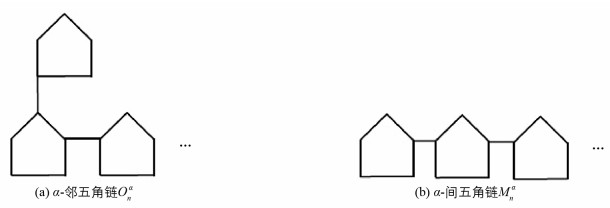
显然，如图 7所示的α-邻五角链O_n^α就是R_n^(α)(1)，而α-间五角链M_n^α就是R_n^(α)(0). 于是由定理1得：

推论1  α-邻五角链O_n^α和α-间五角链M_n^α的Randić 指标分别为

定理2  设R_n^(β)(p₁)是一个n长的β-随机五角链，其中n≥2，则

证  证明方法与定理1完全相似，不再赘述.

定理3  设R_n^(γ)(p₂)是一个n长的γ-随机五角链，其中n≥2，则

证  证明方法与定理1完全相似，不再赘述.

下面考虑t-五角链集(t∈{α，β，γ})的Randić 指标的均值.

设PC_n^(t)是n长的t-五角链的集合(t∈{α，β，γ})，则PC_n^(t)的Randić 指标的均值定义为

因在PC_n^(t)中每个t-五角链出现的概率相等，即

故由定理1、定理2、定理3分别可得下列定理4、定理5、定理6.

定理4  n长的α-五角链集PC_n^(α)的Randić 指标的均值为

注1  由定理1和推论1易得，{O_n^α，M_n^α}的Randić 指标的均值

定理5  n长的β-五角链集PC_n^(β)的Randić 指标的均值为

定理6  n长的γ-五角链集PC_n^(γ)的Randić 指标的均值为

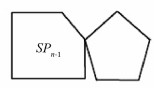
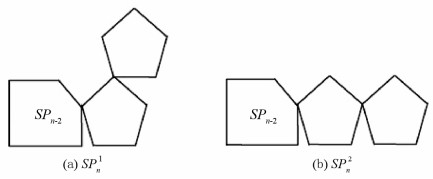
定义4  一个n长的螺旋五角链SP_n是指通过收缩α-五角链B_n的所有割边所得的五角链(如图 8). 当n≥3时，在SP_n-1后添加一个五边形有两种方式，分别记为SP_n¹，SP_n²(如图 9). 因从SP_k-1到SP_k是随机选择(k=3，4，…，n)，故将末端逐步添加五边形的螺旋五角链称为随机螺旋五角链. 假设SP_k-1到SP_k¹，SP_k²的概率分别为p₃，1-p₃(k=3，4，…，n). 令SP_n(p₃)表示由n个五边形构成，且从SP_n-1到SP_n¹的概率为p₃的随机螺旋五角链.

注意到螺旋五角链的边只可能是(2，2)，(2，4)，(4，4)，由Randić 指标的定义得

故计算SP_n(p₃)的Randić 指标取决于m_2，2(SP_n)，m_2，4(SP_n)和m_4，4(SP_n)的值. 显然R(SP_n(p₃))为随机变量，令其期望为E_n=E[R(SP_n(p₃))].

定理7  设SP_n(p₃)是一个n长的随机螺旋五角链，其中n≥2，则

证  当n=2时，通过直接计算可得

当n>2时，m_2，2(SP_n)，m_2，4(SP_n)及m_4，4(SP_n)的值可由图 9中的两种结构来确定.

情形1  设SP_n-1到SP_n¹的概率为p₃，则

因此由(5)式得

情形2  设SP_n-1到SP_n²的概率为1-p₃，则

因此由(5)式得

结合(6)，(7)两式得

又因E[E_n]=E_n，应用期望算子可得

注意到(8)式为一阶常系数非齐次差分方程，显然其所对应的齐次方程的通解为E=C₁，这里C₁为常数.令E′=sn是(8)式的一个特解，将其代入(8)式可得

从而(8)式的通解为

由初始条件E[R(SP₂)]=3+$\sqrt{2}$得

故当n≥2时，有

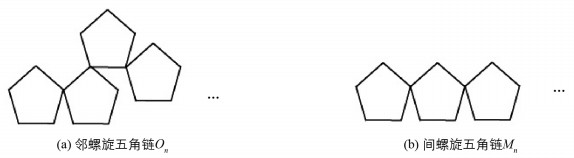
显然，如图 10所示的邻螺旋五角链O_n就是SP_n(1)，而间螺旋五角链M_n就是SP_n(0). 故由定理7得：

推论2  邻螺旋五角链O_n和间螺旋五角链M_n的Randić 指标分别为

接下来考虑螺旋五角链集的Randić 指标的均值. 设SC_n是n长的螺旋五角链的集合，则SC_n的Randić 指标的均值定义为

注意到，在集合SC_n中每个螺旋五角链出现的概率相等，即p₃=1-p₃=$\frac{1}{2}$，故由定理7得：

定理8  n长的螺旋五角链集SC_n的Randić 指标的均值为

注2  由定理7和推论2易得{O_n，M_n}的Randić 指标的均值为