Yamabe Problem on High Dimensional Spherical Cap

球极投影σ：Sⁿ-{N}→$\mathbb{R}$ⁿ将Sⁿ上(除北极点N外)任意一点P(ξ¹，…，ξⁿ，τ)通过北极点N(0，…，0，1)映照到欧氏空间$\mathbb{R}$ⁿ上的一点U(u¹，…，uⁿ). 我们知道，σ^-1可写为

其中$|u|^{2}=\sum\limits_{i=1}^{n}\left(u^{i}\right)^{2}$.

在球极投影下，球面上的标准度量表示为

其中ξ_E是欧氏空间上的标准度量. 在欧氏空间$\mathbb{R}$ⁿ的笛卡尔坐标系下，ξ_E=δ_αβdu^α⊗du^β，从而

我们知道，数量曲率在共形变换$\tilde{g}=\psi^{\frac{4}{n-3}} g$下的变换公式为

球面的标准度量h是一个Einstein度量，任何与h共形且具有常数量曲率的度量也是Einstein度量. 由于这个度量的Weyl曲率是0，因此它具有常截面曲率. 所以这个度量与标准度量是等距的. 我们利用标准球面Sⁿ上的球极投影，以及$\mathbb{R}$ⁿ上的伸缩、平移、旋转变换，构造出球面Sⁿ上的共形变换，从而得到以下结果：

若(Sⁿ，h)是维数n≥3的标准单位球面，设$g=\phi_{0}^{\frac{4}{n-2}} h \in[h]$. 标准单位球面上的Yamabe方程为

该方程在λ=n(n-1)时具有标准解

其中β>1，x₀是球面上的一点^[14].

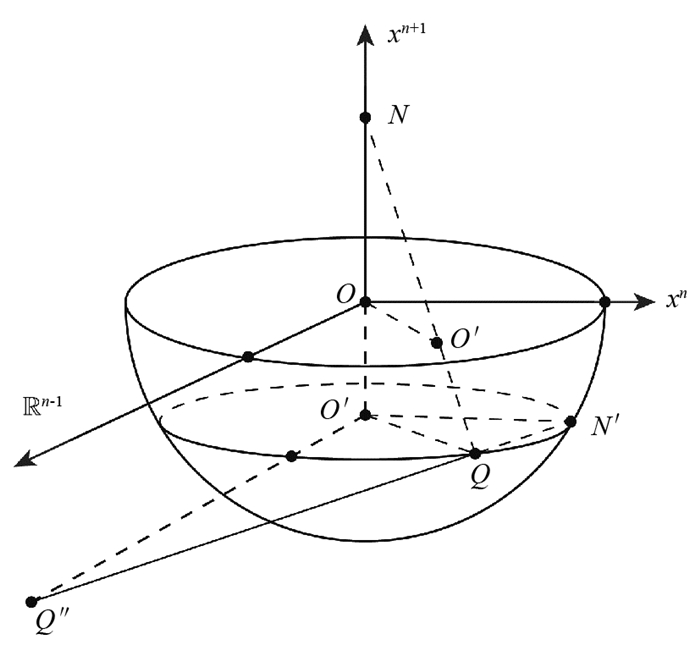
如图 1，令球冠M的半径为r(r≤1)，其边界为∂M. 令h是球面上的标准度量在球冠上的限制，g=φ^*h是通过包含映射φ：∂M→M得到的球冠边界上的诱导度量.

第一次球极投影σ以N(0，…，0，1)为投影中心，将点Q(x¹，…，xⁿ，$-\sqrt{1-r^{2}}$)映到点Q′(u¹，…，uⁿ，0)，计算得到

第二次球极投影$\tilde{\sigma}$以$ N^{\prime}\left(0, \cdots, r, -\sqrt{1-r^{2}}\right)$为投影中心，将球冠边界上任意一点Q(x¹，…，xⁿ，$-\sqrt{1-r^{2}}$)映到点Q″(v¹，…，v^n-1，0，$-\sqrt{1-r^{2}}$)，计算得到

引理1   设h_αβ(α，β=1，…，n)是球面Sⁿ上标准度量h在球极投影σ下的分量，g_ij(i，j=1，…，n-1)是h球冠边界∂M的诱导度量g在球极投影$\tilde \sigma $下的分量，则

证   将球极投影(6)，(7)式进行复合，得到包含映射φ：∂M-{N′}→Sⁿ-{N}的表达式

则

计算得到

由于g=φ^*h，所以

而$h_{\alpha \beta}=\frac{4}{\left(|u|^{2}+1\right)^{2}} \delta_{\alpha \beta}$，其中$|u|^{2}=\sum\limits_{\alpha=1}^{n}\left(u^{\alpha}\right)^{2}$，故

引理1得证.

我们接下来考虑球冠边界上Yamabe方程的解. 如果在球冠(M，h)上给出一个h的共形度量$\tilde h=\phi^{\frac{4}{n-2}} h$，则在球冠(M，h)上的Yamabe方程为

这个方程在h是球面标准度量的情况下是有标准解的. 由引理1可知，在给出h的共形度量下，球冠边界也诱导出相应的共形度量

由于球冠边界比球冠低一维，于是令$\bar{\phi}(x)=\phi^{\frac{n-3}{n-2}}(x), x \in \partial M$，那么

所以在边界(∂M，g)上，Yamabe方程为

定理1   对于球冠M(n=dim M≥4)，带边界条件的Yamabe方程

有解，其中λ，λ是常数，$\bar{\phi}(x)=\phi^{\frac{n-3}{n-2}}(x), x \in \partial M$.

证   由球冠边界的度量，我们很容易得到球冠边界(∂M，g)(n=dim M≥4)的数量曲率S_g. 由(1)式与引理1可知

令

由(6)式可知，在球冠边界上$|u|^{2}=\frac{r^{2}}{\left(1+\sqrt{1-r^{2}}\right)^{2}}$，因此A是常数. 令

从而可得

考虑共形变换$g_{i j}=\psi^{\frac{4}{n-3}} \delta_{i j}$. 我们知道，欧氏空间的数量曲率S_ξE=0，所以欧氏空间的拉普拉斯算子

由(3)式得到球冠边界的数量曲率

我们知道，标准球面Sⁿ上的Yamabe方程具有标准解

其中β>1，x₀是与球面上北极点相关的点，x是球面上任意一点. 那么这个解同样适用于球冠(Mⁿ，h)上，即满足

其中λ=n(n-1).

当这个共形变换只由伸缩、旋转生成时，易知x₀为北极点N或南极点S，此时ϕ₀是旋转对称的. 当限制在球冠边界∂M上时，ϕ₀为常数，记为Λ，从而

因此Δ_gϕ₀=0. 从而

由(14)式可知

即在球冠边界∂M上，满足

其中

我们将流形内部的几何性质与边界的几何性质相联系，提出了球冠上的Yamabe方程的一类边界条件，利用球面Yamabe方程的解，构造出球冠上相应边值问题的解. 这样的结果能否推广到一般的带边界流形以及如何推广，还有待进一步研究.