A Class of Primal-Dual Algorithms Based on BB Step Size

考虑如下二次凸优化问题：

其中$\boldsymbol{S} \in \mathbb{R}^{n \times n}, \boldsymbol{b} \in \mathbb{R}^n, \boldsymbol{c} \in \mathbb{R}^m, \boldsymbol{A} \in \mathbb{R}^{m \times n}$. 在本文中，我们作出如下假设：

(A1) $ \boldsymbol{S} \in \mathbb{R}^{n \times n}$为对称正定矩阵；

(A2) rank(A)=m.

问题(P)的Lagrange函数$\mathscr{L}: \mathbb{R}^n \times \mathbb{ R }^m \longrightarrow \mathbb{ R } $定义为

向量λ称为对偶变量或者原问题(P)的Lagrange乘子向量.

Lagrange对偶函数定义为

问题(P)的对偶问题定义为

引理1^[2]  对于凸优化问题(P)，若条件(A1)-(A2)成立，那么x^*，λ^*分别是原、对偶问题的全局最优解当且仅当

称满足(2)式的(x^*，λ^*)为KKT对. 由引理1知求解凸优化问题(P)的KKT对等价于求解原问题与对偶问题的最优解.

优化问题(P)的增广Lagrange函数为：

其中ρ>0是罚参数. 同样，可利用其增广Lagrange函数定义对偶函数：

引理2^[12]  若x^*，λ^*分别为增广Lagrange函数$\mathscr{L}_p(\boldsymbol{x}, \boldsymbol{\lambda}) $对应的原始、对偶问题的解，则(x^*，λ^*)为Lagrange函数$\mathscr{L}_p(\boldsymbol{x}, \boldsymbol{\lambda}) $的KKT对.

下面我们回顾经典的增广Lagrange乘子算法. 求解问题(P)的增广Lagrange乘子法(ALM)的迭代格式如下：

该算法中的步长ρ是固定的，而罚参数若选取不当，会显著增加求解时间. 为改进算法，考虑用BB算法的步长α_BB去替代固定的步长ρ. 给定$ \boldsymbol{x}_k, \boldsymbol{x}_{k-1}, \boldsymbol{\lambda}_k, \boldsymbol{\lambda}_{k-1}$，定义

其中$\boldsymbol{s}_{k-1}=\boldsymbol{\lambda}_k-\boldsymbol{\lambda}_{k-1}, \boldsymbol{y}_{k-1}=\boldsymbol{A} \boldsymbol{x}_k-\boldsymbol{A} \boldsymbol{x}_{k-1} $. 利用α_BB^k的定义方式，我们得到如下ALM-BB算法.

在本节，我们证明算法2的收敛性. 首先，我们证明算法2中更新Lagrange乘子的过程等价于求增广Lagrange函数对应的对偶问题的BB算法.

定理1  若条件(A1)-(A2)成立，则算法2中更新Lagrange乘子的过程等价于求增广Lagrange函数对应的对偶问题的BB算法.

证   由条件(A1)，对任意给定的$\boldsymbol{\lambda} \in \mathbb{R}^m $，存在唯一的$ \boldsymbol{x} \in \mathbb{R}^n$使得

由于$ \boldsymbol{x} \longmapsto \mathscr{L}_p(\boldsymbol{x}, \boldsymbol{\lambda})$为可微凸函数，由一阶最优性条件可得：

由此可得x的显式表达式：

其中$ \boldsymbol{R}=\boldsymbol{S}+\rho \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}, \boldsymbol{h}=\rho \boldsymbol{A}^{\mathrm{T}} \boldsymbol{c}+\boldsymbol{b}$. 因此对偶函数

其中C为与x，λ无关的常数项.

由(4)式，增广Lagrange函数对应的对偶问题可写为如下无约束凸二次优化问题(为简单起见，我们将常数项C省略，它对对偶问题最优解的求解不会产生影响)：

在假设条件(A1)-(A2)下，矩阵AR^-1A^T是对称正定矩阵，因此优化问题(5)的解存在唯一.

由文献[8]，求解无约束凸优化问题(5)的BB算法迭代格式为

这里$ \widetilde{\alpha}_{\mathrm{BB}}^k=\frac{\left\langle\boldsymbol{s}_{k-1}, \boldsymbol{s}_{k-1}\right\rangle}{\left\langle\boldsymbol{s}_{k-1}, \boldsymbol{y}_{\lambda_{k-1}}\right\rangle}, \boldsymbol{s}_{k-1}=\boldsymbol{\lambda}_k-\boldsymbol{\lambda}_{k-1}, \boldsymbol{y}_{\lambda_{k-1}}=\boldsymbol{g}\left(\boldsymbol{\lambda}_k\right)-\boldsymbol{g}\left(\boldsymbol{\lambda}_{k-1}\right), \boldsymbol{g}\left(\boldsymbol{\lambda}_k\right)=\nabla\left(-\tilde{d}_\rho\left(\boldsymbol{\lambda}_k\right)\right)=\boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{\lambda}_k+\boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{h}- \boldsymbol{c}$.

在ALM-BB算法第2步中，利用凸优化问题的一阶最优性条件可得x_k+1的精确解为

将(7)式代入ALM-BB算法第3步，则有

对比算法2与对偶问题的BB算法，我们只需证明

其中x_k+1为算法2中求得的子问题的最优解.

事实上，由凸优化问题的一阶最优性条件可知x_k+1应满足

利用之前的记号可得

故由(5)式中$ -\widetilde{d}_\rho(\boldsymbol{\lambda})$的定义，有

下面我们利用BB算法的收敛性结果证明算法2产生的迭代序列的收敛性.

定理2   设条件(A1)-(A2)成立，则由算法2得到的迭代序列{(x_k，λ_k)}收敛到原问题的KKT对(x^*，λ^*). 特别地，x^*为原问题的最优解.

证   由条件(A1)-(A2)知x^*为原问题的最优解等价于存在λ^*使得(x^*，λ^*)为KKT对，即(x^*，λ^*) 满足

根据BB算法的收敛性(见文献[13]定理2.5)及定理1，有$\boldsymbol{\lambda}_k \rightarrow \boldsymbol{\lambda}^*, k \rightarrow \infty $. 其中λ^*为对偶问题(5)的最优解. 因此，由一阶最优性条件，

另一方面，由x_k+1的精确表达式(8)及{λ_k}的收敛性知$\boldsymbol{x}_{k+1} \rightarrow \boldsymbol{x}^*, k \rightarrow \infty $，其中

结合(9)式和(10)式可得

即(x^*，λ^*)满足条件$\nabla_\lambda \mathscr{L}\left(\boldsymbol{x}^*, \boldsymbol{\lambda}^*\right)=\bf{0} $.

进一步，

由(10)式和(11)式可得

故(x^*，λ^*)为原问题的KKT对.

此外，利用BB算法的R-线性收敛率，知ALM-BB也具有R-线性收敛率.

设$ T>0, \mathbb{R}^n \text { 与 } \mathbb{R}^m$分别为n维与m维欧式空间，考虑如下线性控制系统：

其中：$ \boldsymbol{A} \in \mathbb{R}^{n \times n}, \boldsymbol{B} \in \mathbb{R}^{n \times m}$；$\boldsymbol{x}(\cdot) $为系统的状态，$\boldsymbol{u}(\cdot) $为系统的控制，$\boldsymbol{x}_0 \in \mathbb{R}^n $是给定的初值，$ \boldsymbol{x}_T \in \mathbb{R}^n$为给定的终值. 称$\boldsymbol{x}(T)=\boldsymbol{x}_T $为终端状态约束. 定义性能指标：

定义可行控制集$ \mathscr{U}:=\left\{\boldsymbol{u}(\cdot):[0, T] \longrightarrow \mathbb{R}^m \mid \boldsymbol{u}(\cdot)\right. \text { Lebesgue }$可测，$ \left.\|\boldsymbol{u}\|_{L^2}^2=\int_0^T|\boldsymbol{u}(t)|^2 \mathrm{~d} t <\infty\right\}$. 带约束的范数最优控制问题是：寻找控制$ \hat{\boldsymbol{u}}(\cdot) \in \mathscr{U}$及控制系统(12)相应于$\hat{\boldsymbol{u}}(\cdot) $的满足约束条件的状态$\hat{\boldsymbol{x}}(\cdot) $，使得

若$ \hat{\boldsymbol{u}}$是上述问题的解，则称$ \hat{\boldsymbol{u}}$为最优控制，相应的状态$ \hat{\boldsymbol{x}}$称为最优状态.

下面，我们给出范数最优控制问题(14)的离散格式. 对控制系统(12)中的线性微分方程，我们有x(T)的显示表达式：

记$ \boldsymbol{\eta}=\mathrm{e}^{\boldsymbol{A} T} \boldsymbol{x}_0, \boldsymbol{M}(t)=\mathrm{e}^{\boldsymbol{A}(T-t)} \boldsymbol{B}$. 则状态约束可表示为：

将(15)式中的积分表达式采用分段常量的逼近策略，取

其中$0=t_0 <t_1 <\cdots <t_N=T $定义如下：

可得如下近似方程：

若记$ \boldsymbol{u}=\left(\boldsymbol{u}^{\mathrm{T}}\left(t_0\right), \boldsymbol{u}^{\mathrm{T}}\left(t_1\right), \cdots, \boldsymbol{u}^{\mathrm{T}}\left(t_{N-1}\right)\right)^{\mathrm{T}}$. 在适当的可积性条件下，可得：

其中

由此可得，范数最优控制问题(12)对应的离散优化问题为：

其中

我们对线性系统(12)作如下假设.

(A3) 线性系统(12)完全能控，即秩条件$ \operatorname{rank}\left(\boldsymbol{A}, \boldsymbol{B} \boldsymbol{A}, \cdots, \boldsymbol{B}^{n-1} \boldsymbol{A}\right)=n$成立.

在条件(A3)下，最优控制问题(14)解存在唯一，并且其离散优化问题(16)中的矩阵S，M满足假设条件(A1)-(A2).

引理3^[14]  设$\hat{\boldsymbol{u}} \text { 与 } \tilde{\boldsymbol{u}} $分别是问题(14)与(16)的最优解，记$\tilde{\boldsymbol{u}}(t)=\sum\nolimits_{i=1}^{N-1} \hat{\boldsymbol{u}}\left(t_i\right) \boldsymbol{X}_{\left[t i-1, t_i\right)} $，则

其中C为常数.

由引理3，求原范数最优控制问题(14)可转化为求凸优化问题(16). 进一步，在假设条件(A3)下，我们可用ALM-BB算法求解问题(16). 下面我们给出一个具体的算例，并用它对原始的ALM与ALM-BB算法进行比较.

例6   设T=3，n=2，m=1，考虑如下控制系统：

及性能指标

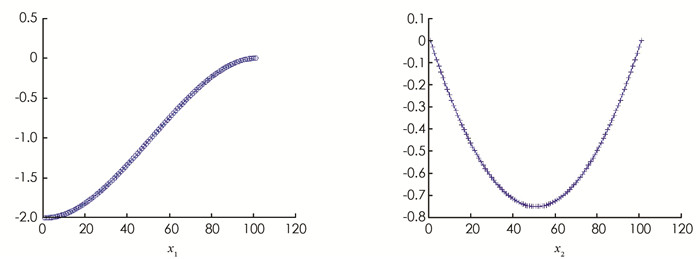
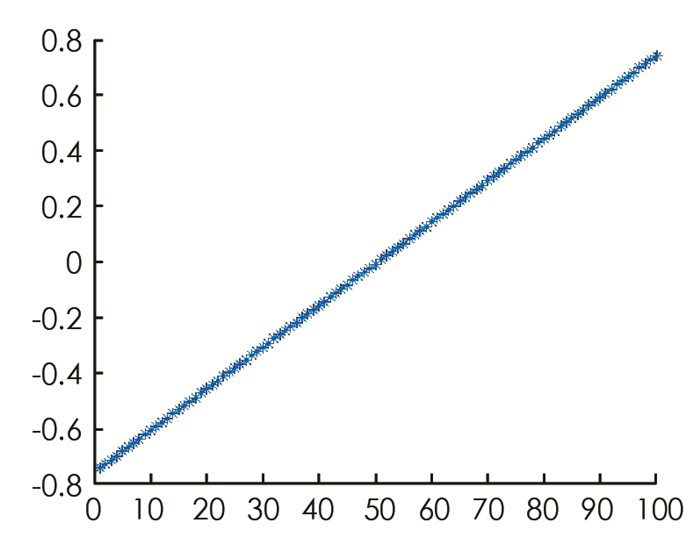
其中$ \boldsymbol{A}=\left(\begin{array}{cc} 0 & -1 \\ 0 & 0 \end{array}\right), \boldsymbol{B}=\left(\begin{array}{l} 0 \\ 1 \end{array}\right), \boldsymbol{x}_0=\left(\begin{array}{c} -2 \\ 0 \end{array}\right)$是初始状态，$\boldsymbol{x}_T=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) $为终端状态约束. 我们直接利用算法2计算其对应的离散优化问题(16)，其中N=100，初始迭代点为$\boldsymbol{u}_0=(3, 3, \cdots, 3), \boldsymbol{\lambda}_0=\left(\begin{array}{l} 1 \\ 5 \end{array}\right) $，算法停止误差ε=10^-6. 计算结果见图 1，2，其中图 1为两个分量x₁与x₂的最优状态图像，图 2为最优控制的图像.

为了说明ALM-BB算法的有效性，我们选择不同的罚参数和划分细度进行计算，将ALM-BB和ALM算法的计算时间和迭代次数对比见表 1.

由表 1可以看出，在划分细度与罚参数相同的情况下，ALB-BB算法迭代步数更少，收敛速度更快. 但是当罚参数选取过大时，ALM与ALM-BB算法运行时间差别不大，对罚参数的选取依然敏感.

本文通过改变ALM算法中更新乘子这一迭代步的步长来提高算法的收敛速度. 范数最优控制问题本质上是无穷维的二次凸优化问题，通过适当的离散格式可以将其转为有限维的二次凸优化问题. 通过求解范数最优控制问题的数值算例发现，ALM-BB算法较ALM计算效率更高. 从数值实验看出ALM-BB算法的数值表现仍依赖于参数的选取. 此外，本文的收敛性证明依赖于凸二次规划问题的具体结构以及子问题可精确求解，对于更一般的非精确的ALM-BB算法的收敛性有待进一步研究.