Exploring a Class of Reversible Reactions with the "anti" Le Chatelier Principle

为了让推导过程易于理解，参考大学教材可使用压力平衡常数(K_p)和压力熵(Q_p)判断平衡移动方向^[7]. K_p可以用平衡时各物质的分压计算得到，表示方法如下：对于一般的可逆反应mA+nB⇌hC+kD，在一定温度下，$K_{\mathrm{p}}=\frac{p^h(\mathrm{C}) \cdot p^k(\mathrm{D})}{p^m(\mathrm{~A}) \cdot p^n(\mathrm{~B})}$，其中p(A)，p(B)，p(C)，p(D)分别表示平衡时各气体的分压. 该常数只随温度的变化而变化，而不随浓度和压力的变化而变化. 用压力平衡常数(K_p)和压力熵(Q_p)的相对大小也可判断平衡移动的方向，压力熵表示为$Q_{\mathrm{p}}=\frac{p^h(\mathrm{C}) \cdot p^k(\mathrm{D})}{p^m(\mathrm{~A}) \cdot p^n(\mathrm{~B})}$.

当Q_p < K_p时，化学反应正向进行；当Q_p=K_p时，化学反应达到平衡；当Q_p>K_p时，化学反应逆向进行^[5].

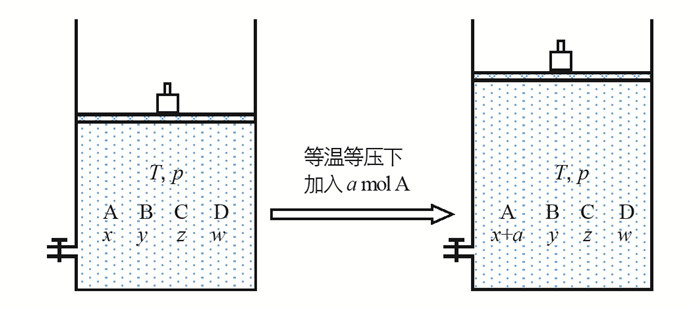
利用K_p和Q_p的相对大小可解决用勒夏特列原理解释不了的问题. 对于一般的可逆反应A+(h+k+1)B⇌hC+kD，在等温(T)等压(p)条件下达到平衡后，再加入a mol A(图 1)，平衡可能正向移动、不移动或者逆向移动. 具体情况如何，需计算比较Q_p与K_p的相对大小来加以判断.

用两段式表示为：A+(h+k+1)B⇌hC+kD

其中x，y，z，w和a均为正数.

在平衡态时，

在新状态时，

当Q_p>K_p时,

Ⅰ. 当y+z+w≤x时，即平衡时$\varphi_{\mathrm{A}} \geqslant \frac{1}{2}$，(1)式恒成立，即Q_p>K_p，在y+z+w≤x的情况下$\left(\varphi_{\mathrm{A}} \geqslant \frac{1}{2}\right)$恒成立，平衡一定逆向移动.

Ⅱ. 当y+z+w>x时，即$\varphi_{\mathrm{A}}<\frac{1}{2}$，且$a>\frac{(x+y+z+w)(y+z+w-x)}{x}$，此时Q_p>K_p，平衡逆向移动.

同理可推出以下另外两种情况.

Ⅲ. 当y+z+w >x时，即$\varphi_A<\frac{1}{2}$，且$a=\frac{(x+y+z+w)(y+z+w-x)}{x}$，此时Q_p=K_p，平衡不移动.

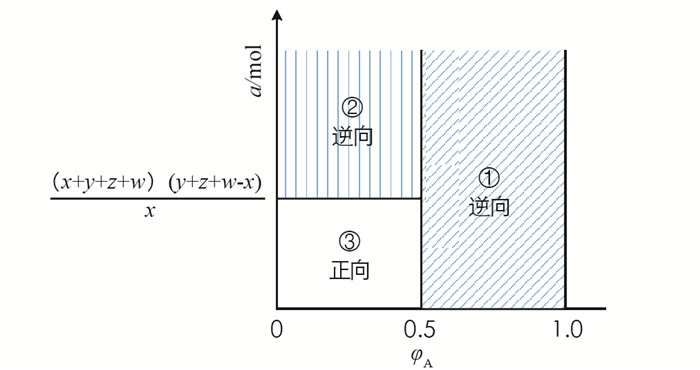
Ⅳ. 当y+z+w >x时，即$\varphi_A<\frac{1}{2}$，且$ a<\frac{(x+y+z+w)(y+z+w-x)}{x}$，此时Q_p < K_p，平衡正向移动.

综上，对于一般的可逆反应A+(h+k+1)B⇌hC+kD，在等温(T)等压(p)条件下达到平衡时有x mol A，y mol B，z mol C和w mol D，再通入a mol A，当φ_A和a处于如图 2所示的①区域，平衡逆向移动. 另外，发现当φ_A和a的值处于②区域，此时$\varphi_A<\frac{1}{2}$且$a>\frac{(x+y+z+w)(y+z+w-x)}{x}$，平移依然逆向移动，扩大了再加反应物平衡逆向移动的投料范围. 研究发现表 1中的反应都符合上述结论，从而拓宽了该结论的应用范围.

表 1中各反应在等温(T)等压(p)条件下达到平衡后，再加入A，当处于图 2中①和②区域，化学平衡逆向移动，出现“反”勒夏特列原理的现象. 这与文献[8]中提到“存在反常的勒夏特列原理”一致，只不过文献中并没有归纳出更多例具体反应，也没有推导出“违背”勒夏特列原理所需反应物的投料范围. 实际上再加入A，A的物质的量分数较大时，一方面由于体积变大使得B的分压减小，而B的化学计量数较大，使得B分压下降的影响较大，从而使平衡逆向移动；另一方面，A投料时浓度较大，大到一定程度时，受限于B浓度下降，A不能再转化成产物. 虽表面上与勒夏特列原理“相悖”，但实际上与勒夏特列原理相符.

N₂+3H₂⇌2NH₃可看作是一类反应A+(h+k+1)B⇌hC+kD中的特殊例子(h=2，k=0). 根据文献[9]得出的工业合成氨条件为投料比n(N₂)∶n(H₂)=1∶3、温度460 ℃、压强10~30 MPa. 根据文献数据^[7]计算得到合成氨反应在460 ℃时的K_p^Θ=1.56×10^-4. 设压强为20 MPa，加入1 mol N₂和3 mol H₂，列出以下的两段式：

根据$K_{\mathrm{p}}^{\ominus}=K_x\left(\frac{20 \mathrm{MPa}}{1 \times 10^5 \mathrm{~Pa}}\right)^{-2}=\frac{\left(\frac{2 x}{4-2 x}\right)^2}{\left(\frac{1-x}{4-2 x}\right)\left(\frac{3-3 x}{4-2 x}\right)^3}\left(\frac{20 \times 10^6}{1 \times 10^5}\right)^{-2}=$=1.56×10^-4，计算得到x=0.515，再加入a mol N₂，平衡态和新状态表示为：

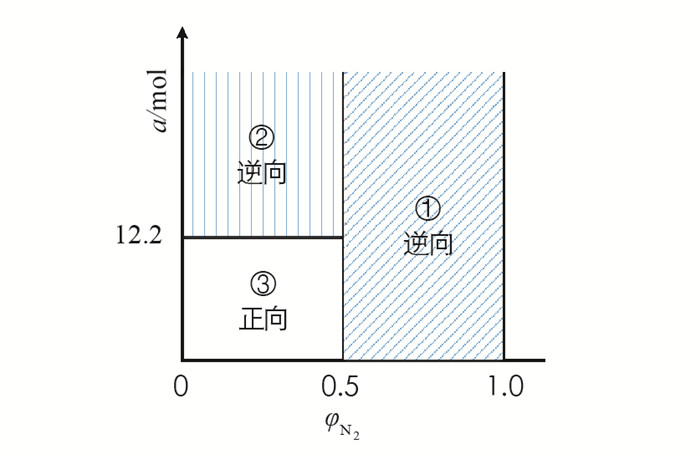
平衡态时N₂的物质的量分数$\varphi_{\mathrm{N}_2}=\frac{0.485}{2.97}=0.163<\frac{1}{2}$，故工业合成氨中不存在$\varphi_{\mathrm{N}_2} \geqslant \frac{1}{2}$，即不存在图 3中①区域. 根据一类反应A+(h+k+1)B⇌hC+kD的结论可推出工业合成氨中存在的3种可能性.

Ⅰ.$\varphi_{\mathrm{N}_2}<\frac{1}{2}, a>\frac{(x+y+z)(y+z-x)}{x}=$$\frac{(0.485+1.455+1.030)(1.455+1.030-0.485)}{0.485}$，此时Q_p>K_p，平衡逆向移动.

Ⅱ.$\varphi_{\mathrm{N}_2}<\frac{1}{2}$，且$a=\frac{(x+y+z)(y+z-x)}{x}=12.2$，此时Q_p=K_p，平衡不移动.

Ⅲ.$\varphi_{\mathrm{N}_2}<\frac{1}{2}$，且$a<\frac{(x+y+z)(y+z-x)}{x}=12.2$，此时Q_p < K_p，平衡正向移动.

因此，在460 ℃，20 MPa下，加入1 mol N₂和3 mol H₂达到平衡后，当再加入N₂的量大于12.2 mol，平衡逆向移动. 即工业中合成氨反应时不能只增加N₂的投料使平衡正向移动，因为还存在当再加入N₂的物质的量a>12.2 mol时，平衡会逆向移动，存在“反”勒夏特列现象. 故一类反应A+(h+k+1)B⇌hC+kD的结论也适用于特殊例子N₂+3H₂⇌2NH₃(h=2，k=0).

本文讨论了在A+(h+k+1)B⇌hC+kD一类反应中，在等温(T)等压(p)条件下以任意比例投料达到平衡后，当φ_A≥1/2时，无论再加入A的物质的量a为多少，平衡一定逆向移动；还发现当φ_A < 1/2且$a>\frac{(x+y+z+w)(y+z+w-x)}{x}$时，平衡也是逆向移动，拓宽了再加反应物使平衡逆向移动的投料范围. 该“反”勒夏特列原理的结论适用于很多常见反应，包括N₂+3H₂⇌2NH₃. 实际上由于体积增大导致B的浓度下降，限制了A再转化成产物，并且B的化学计量数较大，在压力熵的表达式中影响更大，为了减弱B的分压影响，平衡逆向移动，故本质上与勒夏特列原理相符. 通过对一类具有“反”勒夏特列原理的可逆反应A+(h+k+1)B⇌hC+kD的深入探析，可增强学生的探究意识，打破思维定式，有利于“变化观念和平衡思想”素养的培养，也利于后续其他化学学科的学习.