-
许多物理现象都可以用非线性演化方程来描述,一直以来受到学者的广泛关注和研究. 科学家们运用了各种方法来构造非线性系统的解,并研究发现利用对称方法构造其精确解是一种很有效的方法[1-2]. 文献[3]发现非线性系统Painlevé截断展开的奇异流形的留数是非局域对称,称之为留数对称[3]. 目前,很多方程都可以利用上述方法进行对称约化,如Korteweg-de Vries方程、Kadomtsev-Petviashvili方程、Burgers方程、色散长波方程等[4-11].
本文主要对Tu方程
进行研究,这是文献[12]在对Loop代数
${\tilde {A_1}}$ 进行分析后得到的一族新的可积系统,具有Painlevé可积性质、Hamilton结构和无穷多守恒律等性质,有重要的研究及应用价值. 文献[13-14]利用Tu方程的Painlevé截断展开性质,得到了系统的一些精确解[13-14]. 文献[15]研究了Tu孤子族换位表示的一般结构[15]. 文献[16]得到了Tu方程的几何对称结构[16]. 本文主要研究Tu方程(1)的留数对称,得到方程新的Bäcklund变换,然后证明Tu方程的CRE可解性,并得到该方程的孤立波解.
HTML
-
Tu方程(1)的Painlevé截断展开式为
其中:f表示奇异流形;u0,u1,v0,v1,v2,f都是关于x,t的函数.
将展开式(2)代入到式(1)中,合并f的同次幂,有
令其各次幂项的系数都为零,可解出系数:
同时f需要满足下面的Schwarzian形式:
根据展开式(3),如果{u,v}是方程(1)的解,则f的零次幂的系数为零的表达式说明{u0,v0}也满足Tu方程(1),从而得到如下自Bäcklund变换定理[3]:
定理1如果{u,v}是Tu方程(1)的解,则
就是方程(1)的一个自Bäcklund变换.
我们知道,Schwarzian方程(5)在Möbious变换
的作用下是形式上保持不变的,即方程(5)容许如下的3种对称:
其中c1,c2,c3为任意常数. 特殊地,取a=d=1,b=0,c=-ε,其中ε为任意群参数,则此时Schwarzian方程(5)式的对称为
根据上述分析,可以得到Tu方程的非自Bäcklund变换定理如下.
定理2 如果f是Schwarzian方程(5)的解,则
是f和Tu方程的解{u0,v0}之间的一个非自Bäcklund变换.
-
Tu方程(1)的对称方程为
与式(3)中的奇异流形f的留数作比较,可以知道{u1,v1}为Tu方程(1)的解{u0,v0}的留数对称,即:
其中{u0,v0}和f满足非自Bäcklund变换(7). 为了方便表示,不失一般性,本节我们用{u,v}代替{u0,v0}进行描述. 为将留数对称进行约化,首先对其进行局域化,解决如下初值问题:
其中ε为群参数. 将Tu方程进行适当延拓,引入辅助变量:
则解{u,v}的非局域留数对称(11)可以被局域化,得到延拓系统(1),(5),(13)的Lie点对称,即:
相应的Lie点对称的向量场表达式为
解如下初值问题:
可得到下面的对称群变换定理.
定理3(对称群变换定理) 如果{u,v,f,g,l,h,k}是方程(1),(5),(13)的解,则{
$\hat u, \hat v, \hat f, \hat g, \hat l, \hat h, \hat k$ }也是其解,其中
-
根据CRE方法,Tu方程(1)的解有如下展开式:
其中w=w(x,t),R(w)是Riccati方程:
的解,l0,l1,l2是任意常数. 将表达式(18)和(19)代入方程(1)中,令R(w)的各次幂前面的系数为零,可得
同时,函数w满足下面方程:
由此可知,Tu方程(1)是CRE可解的.
根据孤立波解通常可用双曲函数表示的特点,我们可将该方程用tanh函数展开方法求解. 取式(19)中l0=1,l1=0,l2=-1,此时Riccati方程的特解为
那么可以得到
此时我们称Tu方程是CTE可解的.
为了得到Tu方程的精确解,我们考虑以下两种特殊情形,说明Tu方程的孤立波解的具体形式.
例1 考虑w为如下形式:
其中k,h,b为任意常数,将其代入式(18)及式(1)中,令R(w)的所有次幂的系数为零,得到代数方程组如下:
通过解上述方程组,得到一组非平凡解为
由此得到Tu方程(1)的孤立波解为
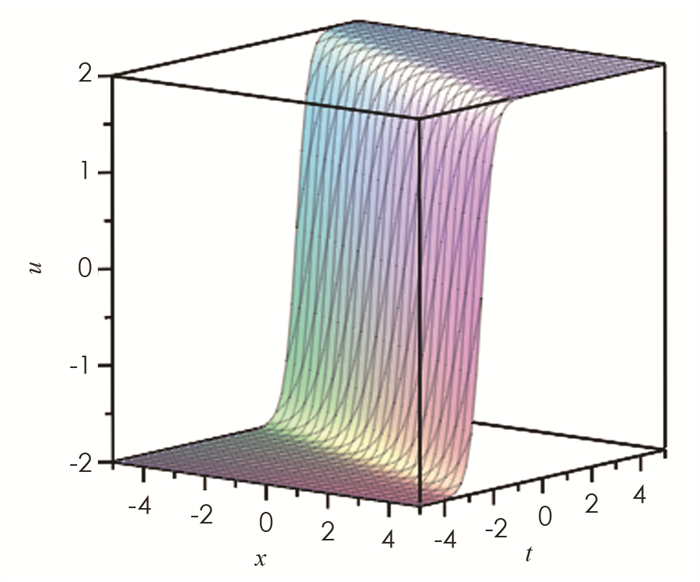
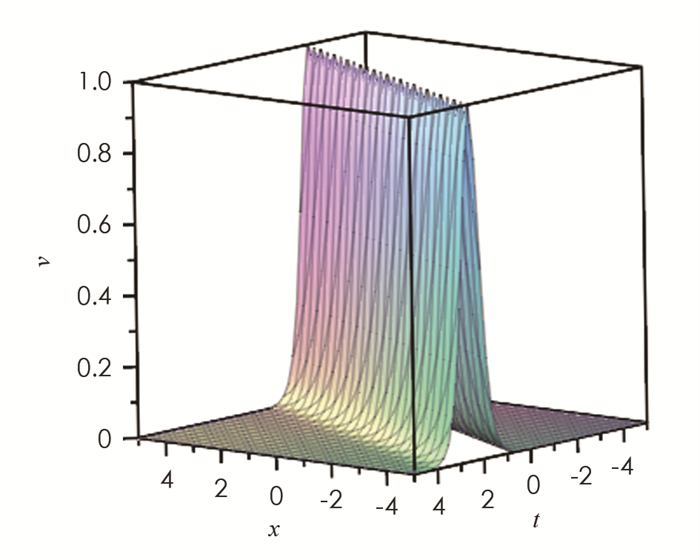
取参数值{k=1,h=3,b=0},利用MAPLE软件,我们得到孤立波相互作用解的波形图. 图 1为解u的波形图,是反扭结型孤立波,图 2为解v的波形图,是钟型孤立波.
例2 我们考虑w具有如下形式:
其中k1, k2, h1, h2都是任意常数,将式(28)代入式(21)中,我们发现W1=WX满足如下椭圆方程:
式中
其中h1,h2,C2,C3为任意常数. 则Tu方程的解具有如下形式:
接下来讨论方程(1)的非线性波之间的相互作用解. 取方程(29)的解W为如下形式:
其中sn(X,m)为椭圆函数,联立式(1),(28),(32)可解得系数的一组非平凡解为:
因此方程的解为
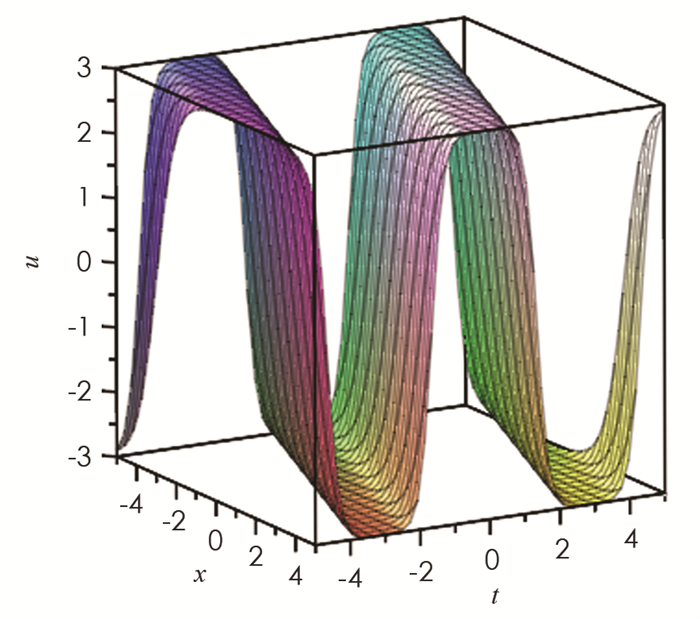
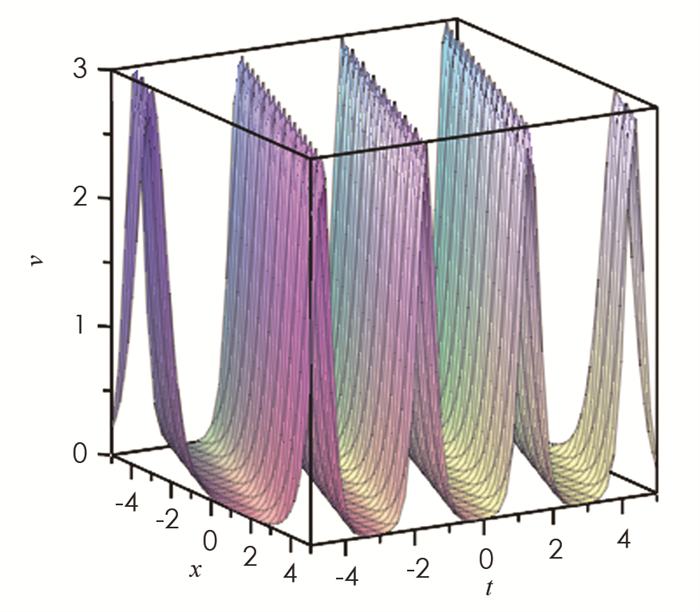
参数取值为{m=0.999,k2=1,h2=3},利用MAPLE软件,我们得到Tu方程(1)解的波形图,其中:图 3为解u的波形图,描述了椭圆周期波和反扭结型孤立波的相互作用;图 4为解v的波形图,描述了椭圆周期波和钟型孤立波的相互作用.
-
本文首先得到Tu系统的非局域留数对称,并分析其Bäcklund变换,通过引入合适的新变元将其局域化后利用Lie的第一基本定理得到了有限变换定理. 之后说明了Tu系统具有CRE可解性,并利用MAPLE软件作图描述Tu系统的不同形状的孤立波和周期波之间的相互作用.






 DownLoad:
DownLoad: