下面，我们引出Hilbert空间：

‖·‖_k和|·|_k分别表示通常的Sobolev空间H ^k(Ω)^d(k≥0) 的范数和半范数，(·，·)表示L²(Ω)^d(d=1，2，3) 的标准内积.定义三线性形式：b(u，v，w)=((u·▽)v，w)，∀u，v，w ∈X.其满足下列性质^[4]：

其中：当d=2时，s=ε为任意小；当d=3时， $s=\frac{1}{2}$ .

考虑方程(1)-(3) 的变分形式：求解(u，p)∈X×M，使得满足

其中双线性形式(▽· v，p)在X×M上是连续的且满足著名的inf-sup条件：存在一个常数β＞0使得

引理 1 ^[3] 设X′是H₀¹(Ω)^d的对偶空间，f∈X′，方程(1)-(3) 存在一个非奇异解u满足

设T^μ(Ω)={K}(μ=H，h且H＞h)是Ω的一个网格剖分.细网格T^h(Ω)是粗网格T^H(Ω)的加密.基于T^μ(Ω)={K}的有限元空间对(X_μ，M_μ)满足下列假设：

(A1) 逼近性：对任何(u，p)∈(H₀¹(Ω)∩H^k+1(Ω))^d×(L₀²(Ω)∩H^k(Ω))，满足

(A2) inf-sup条件：存在一个常数β＞0使得

这里P₁是次数不超过1的多项式空间.亚格子模型基于一个椭圆算子Π_μ：X→R₁其定义为^[6]

保持如下估计^[7]：

利用投影算子，我们定义亚格子稳定化项：

这里0＜α＜1是一个稳定化参数.定义连续双线性形式：

为了方便后面定理的推导，给出引理2，3，推导过程可参考文献[4].

引理 2 存在一个不依赖于h，H的常数γ＞0满足：

为了误差分析的需要，我们引进Galerkin投影(Q，R)：Y→Y^H如下：

引理 3 投影(Q，R)满足下列性质：

(ⅰ) |||(v-Q(v，q)，q-R(v，q))|||≤C|||(v，q)|||，∀(v，q)∈Y；

(ⅱ) ||v-Q(v，q)||_θ≤CH^1-θ|||(v，q)|||，∀(v，q)∈Y，0≤θ≤1；

(ⅲ) ||v-Q(v，q)||₀+H|q-R(v，q)|₁≤CH²(||v||₂+||q||₁)，∀(v，q)∈Y∩(H ²(Ω)^d×H ¹(Ω)).

算法 1 ^[5] 单水平有限元变分多尺度方法(1-VMS)求解(u_μ，p_μ)∈X_μ×M_μ，使得∀(v，q)∈X_μ×M_μ，满足

引理 4 ^[8] 假设(u，p)是Navier-Stokes方程的非奇异解且满足

当μ→0时α→0.则存在μ₀＞0，使得对于μ≤μ₀，算法1定义的近似解(u_μ，p_μ)满足

算法 2 回溯两水平有限元变分多尺度方法(b-VMS)

步骤1 求解(u_H，p_H)∈X_H×M_H，使得∀(v，q)∈X_H×M_H，满足

步骤2 求解(u ^h，p ^h)∈X_h×M_h，使得∀(v，q)∈X_h×M_h，满足

步骤3 求解(e_H，r_H)∈X_H×M_H，使得∀(v，q)∈X_H×M_H，满足

设置u ^*=u ^h+e_H，p ^*=p ^h+r_H.

此算法中，G_H(u_H，v)形如(11) 式(μ=H)，而G_h^*(u ^h，v)和G_H^**(e_H，v)分别定义如下：

定理 1 在引理4的条件下，算法2第二步的解(u ^h，p ^h)∈X_h×M_h满足：

证 在(20) 式中取(v，q)=(u ^h，p ^h)即可得到第一个结论||▽u ^h||₀≤||f||_-1.从(5) 式中减去(20) 式，得到

设(I^h u，J^h p)∈Y^h是(u，p)的插值，利用三角不等式、A^H的连续性、逼近性(7) 式和引理4得到

定理 2 在引理4和定理1的条件下，算法2的解(u ^*，p ^*)∈X_h×M_h满足：

证 由定理1可知：

其隐含：

根据步骤3和投影(16) 的定义有

从(25) 式减去(26) 式，可得

因为(I^hu-u ^*，J^hp-p ^*) ∈Y^h，利用(15) 式和双线性形式B^H连续性可得

其中对稳定化项的估计是容易的，于是

为了估计(28) 式的剩余部分，定义

进一步有

应用引理3和不等式(4) 有

又由逼近性知

综上所述，可得

注 1 定理1指出如果算法2停留在步骤2，粗细网格的关系为： $h\sim {{H}^{1+\frac{1}{k}}}$ ，k≥1.定理2指出如果算法2进行到步骤3，粗细网格的关系为：

从上面的比较中可以看出，步骤3改善了粗细网格的关系.

注 2 定理2指出算法2参数的选择为：

这部分我们主要通过做一些数值实验来验证算法的高效性，我们设计了两个实验.算法以有限元软件FreeFem++^[10]为平台，网格采用三角形单元，非线性迭代收敛准则为10^-6，粗网格上非线性迭代次数超过5 000视为迭代方法失败.

求解区域Ω=[0, 1]×[0, 1].

首先，为测试本文3种方法的渐近误差，我们在尺寸为 $h=\frac{1}{{{n}^{2}}}$ ， $H={{h}^{\frac{1}{2}}}$ ，(n=6，7，8，9，10，11) 的一致网格上，用回溯两水平有限元变分多尺度方法(b-VMS)计算Navier-Stokes方程的有限元解，这里粘性系数设置为ν=0.01.对(32) 式给出的真解问题，估计(24) 式取k=2.我们用Taly-Hood元，理论预测能量范数的收敛率为 $\mathscr{O}$ (h²).根据注2选择稳定化参数为α=0. 1h².用Newton迭代法求解非线性Navier-Stokes问题.数据结果见表 1，其中it表示满足停机准则的非线性迭代次数.从表 1可以看到我们的方法能得到最优渐近收敛阶，数据结果很好地支持了理论预测.

其次，为了评估本文所提方法的性能，我们分别用单水平有限元变分多尺度方法^[5]，文献[4]中的算法1，两参数稳定化有限元方法^[9]来计算有限元解.数据结果分别列在表 2，表 3，表 4.比较表 1-4，这几种方法的计算近似解的精度相差不是很多，特别地，对于速度近似解而言几乎是相同的.然而，与单水平有限元变分多尺度方法^[5]相比，我们的方法节省了大量的计算时间，当 $h=\frac{1}{{{n}^{2}}}$ (n=6，7，8，9，10，11) 时，分别节省时间74.7%，75.2%，77.3%，78.3%，78.5%，79.3%；与文献[4]中的算法1相比，我们的方法增加了稳定项却没有降低近似解的精度和收敛阶，特别是当粘性系数很小时(ν=0.000 01)，我们的方法工作得很好，而文献[4]中的算法1却是发散的；与两参数稳定化有限元方法^[9]相比，我们的方法用的时间较少，速度解精度也要高一些.

最后，为了验证步骤3的对近似解的贡献，我们把近似计算停留在步骤2.根据定理1可得h= $\mathscr{O}$ ( ${{H}^{\frac{k+1}{k}}}$ )，α= $\mathscr{O}$ (h^k)，对于(32) 式给出的真解问题，估计(22) 式对k=2保持.为了方便比较我们设置粗网格尺寸为 $H=\frac{1}{n}$ (n=6，7，8，9，10，11)，再根据 $h={{H}^{\frac{3}{2}}}$ ，α=0. 1h²，计算出细网格的尺寸和稳定化参数即可带入运行算法，数据结果详见表 1.比较表 1和表 5可以看到，步骤3对近似解的精度有大幅改善.

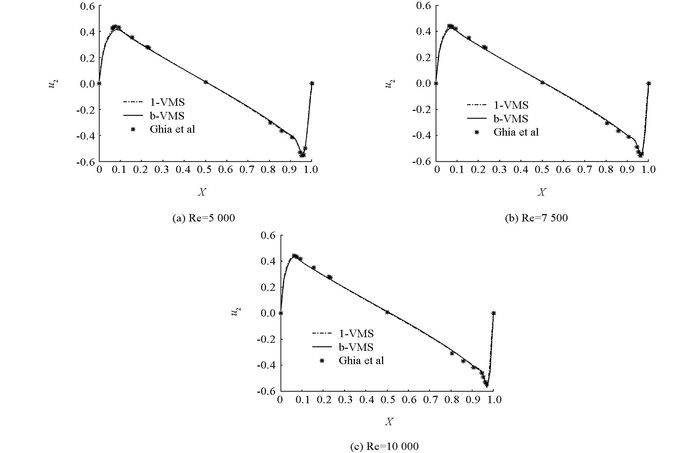
在这个试验中，我们考虑一个定义在单位正方形上的不可压缩方腔驱动流问题.外部体积力f=0，顶盖上的水平速度u₁=1，垂直速度u₂=0，其余三边的速度都为0.这个问题的雷诺数定义为 ${\mathop{\rm Re}\nolimits} {\rm{ = }}\frac{{UL}}{v}$ ，其中U是顶盖速度，L是侧边宽度.

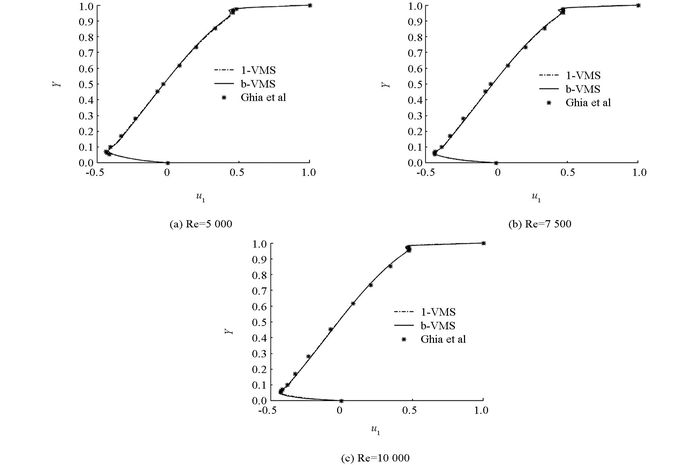
设置网格尺寸为 $h=\frac{1}{128}$ ， $H=\frac{1}{64}$ ，对这个问题，估计(24) 式对k=1保持，设置α=0. 1h.分别取雷诺数为Re=5 000，7 500，10 000.我们分别用单水平有限元变分多尺度方法(1-VMS)^[5]，本文所提算法以及文献[4]中的算法1来模拟方腔驱动流.值得注意的是在这种网格和雷诺数的情况下，文献[4]中的算法1由于在粗网格上的非线性迭代发散因此无法模拟，而前两种方法运行得很好.

我们在图 1-2画出了垂直中心线上的速度分量u₁和水平中心线上的速度分量u₂，与Ghia等人^[11]的数据结果作比较. 图 1-2表明，本文所提算法的精度可以和Ghia等人^[11]的结果相媲美.单水平有限元变分多尺度方法(1-VMS)^[5]和本文所提算法的数据结果没有明显差异，但后者节省了大量的计算时间，详见表 6.

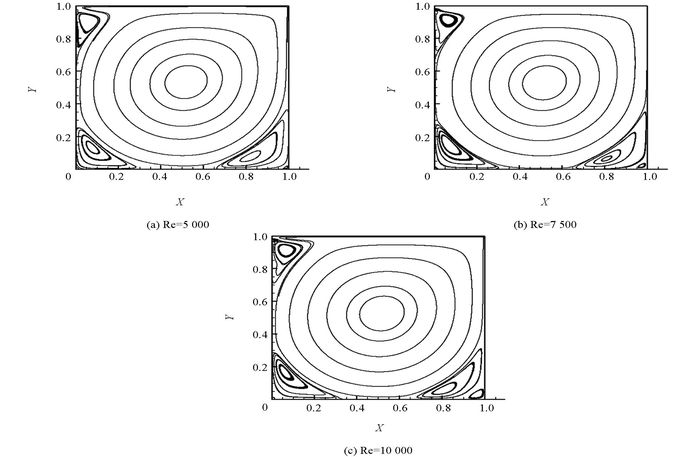
图 3-4描绘了在设置α=0.05 h，取不同雷诺数5 000，7 500，10 000 d的情况下，本文所提方法(b-VMS)模拟得到的线性流和压力等值线，与文献中的相一致，这就证明了此算法的有效性.

我们的方法基于粗网格上的亚格子模型稳定化的Navier-Stokes问题，细网格上的一个稳定化线性Oseen问题和一个回溯到粗网格的完全线性化校正问题.通过适当的稳定化参数和粗细网格尺寸的选取，这些算法能取得最优渐近收敛阶.数值算例验证了其高效性，并且从与普通算法的比较中可以看出，我们的算法性能最为良好，既能够解决大雷诺数问题，又能够节省大量的计算时间.