-
20世纪30年代Elton[1]最初提出了食物网的概念以及研究方法,从此拉开了食物网的研究序幕.随后,学者们广泛地研究了食物网的特征,包括稳定性、复杂性和动力学等特点[2-4],如1991年Hastings和Powell[3]在一个简单的三种群食物链模型中发现了混沌行为;Fussmann和Heber[4]认为食物网系统中营养级越多,混沌的预测就越困难,而且自然食物网的结构特征在本质上可能降低种群动态出现混沌的可能性.因此食物网模型动力学行为的研究,对理解自然生态系统的特性具有关键的作用.
食物网模型是种群动力学中最重要的模型之一[5-6].近年来,具有功能反应的食物网模型引起了人们的广泛关注[5-10],如Baek[5]研究了两种功能反应下的三种群食物网动力系统模型,讨论了系统在平衡点处的稳定性,并根据极限环存在的条件确定了系统的稳定性条件,通过数值模拟展示了Hopf分岔等行为;Raw等人[7]提出并讨论了一个具有防御机制的三种群食物网模型,并发现了许多复杂的动力学行为,如Hopf分岔、拟周期分岔和混沌等.
食物网模型的动力学行为研究是种群动力学的前沿问题之一[7, 11].食物网系统的动力学行为对于揭示种群随时间演化的分布规律有着非常重要的生态学意义.因此,本文基于Hasting-Powell模型[3]构建了Holling-Ⅱ型三种群食物网动力系统模型,其表达式为:
其中:Fi(U)表示Holling-II型功能反应函数,其表达式为
式中:X,Y,Z是种群密度; T是时间;R是种群X的内在增长率;K是环境对种群X的最大承载能力;E1是种群Y捕食种群X的转化率;E2是种群Z捕食种群X的转化率;E3是种群Z捕食种群Y的转化率;I1是种群Y的死亡率;I2是种群Z的死亡率;Ai(i=1,2,3)是捕获率;Bi是饱和率.
从生态学的角度来讲,参数R,K,Ii,Ei,Ai和Bi的值均不小于零,还应注意到种群密度也应不小于零.因此,方程(1)应该限制在
$ \mathbb{R}_{+}^{3}=\left\{(X, Y, Z) \in \mathbb{R}^{3} : X \geqslant 0, Y \geqslant 0, Z \geqslant 0\right\}$ 的状态空间.为了减少方程(1)中参数的数量,对其无量纲化,引入:利用(3)式替换(1)式中的相应变量,可以得到无量纲的食物网系统:
其中:
全文HTML
-
令dx/dt=0,dy/dt=0,dz/dt=0,可以得到系统(4)的唯一共存平衡点E*(x*,y*,z*),且共存平衡点E*满足代数方程:
用Jacobian矩阵和Routh-Hurwitz判据来讨论系统(4)在共存平衡点E*处的局部渐进稳定性.系统(4)在共存平衡点E*处的Jacobian矩阵可写为
那么Jacobian矩阵J(E*)对应的特征方程为
其中,bij为Jacobian矩阵的元素,且
定义
根据Routh-Hurwitz判据,如果条件Δ1>0,Δ2>0和Δ3>0同时满足,那么系统(4)在共存平衡点E*处是局部渐进稳定的.否则,在共存平衡点E*处是不稳定的.
举例验证系统(4)在共存平衡点E*处的局部渐进稳定性.选择参数:
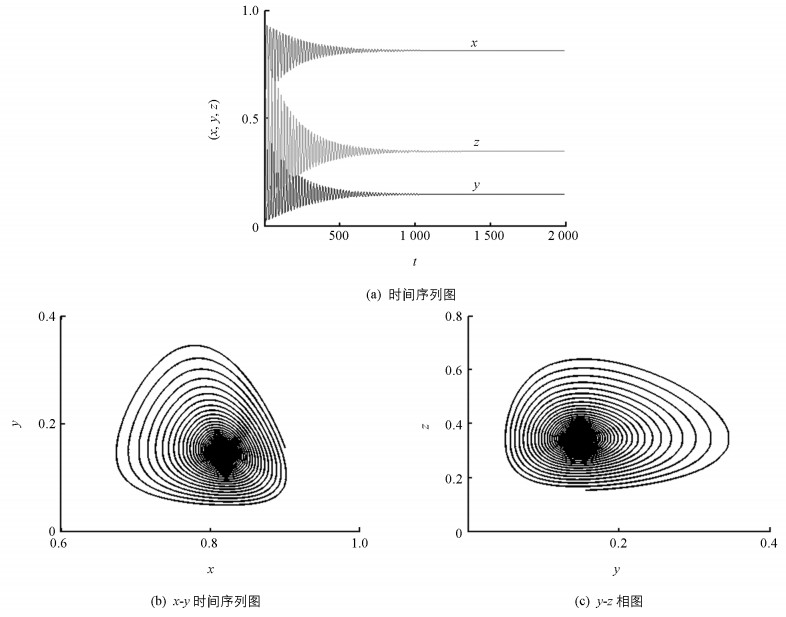
图 1表明系统(4)是局部渐进稳定的,即种群状态随着时间的演化由初始的震荡状态最终趋于稳定平衡(图 1(a));x-y相图(图 1(b))和y-z相图(图 1(c))也表明种群状态最终趋于稳定平衡,即趋于一个稳定的中心.
由(10)式提供的参数可得共存平衡点E*=(0.901 9,0.144 1,0.363 5),那么Jacobian矩阵J(E*)对应特征方程的特征根为:
可见特征根的实部均小于零,表明系统(4)是局部渐进稳定的.
相应地,可以得到:
可见条件Δ1>0,Δ2>0和Δ3>0同时满足,从而进一步表明系统(4)在共存平衡点E*处是局部渐进稳定的.
-
本节将用Hopf分岔理论和中心流形理论[12-15]来确定系统(4)产生Hopf分岔的条件.根据Hopf分岔理论,当系统(4)经历Hopf分岔时,相应的特征方程(7)必须有一对共轭的纯虚根,即
选择参数r作为分岔参数.当参数r的值在Hopf分岔临界点r0附近变化时,纯虚根±iω将变成复特征根λ
$ \lambda=v+i \tilde{\omega}$ ,并将$ \lambda=v+i \tilde{\omega}$ 带入特征方程(7)进行实部和虚部的分离,可得化简(14)式和(15)式,可得
在r=r0处,(16)式对r求导,可得
如果
$ \left.\frac{\mathrm{d} v}{\mathrm{d} r}\right|_{r=r_{0}} \neq 0$ 满足,那么系统(4)将产生Hopf分岔,表明当参数r跨过分岔临界点r0时,种群状态随着时间的演化由稳定平衡变为周期震荡.系统(4)在r=r0处经历Hopf分岔时还应满足最后的决定条件.考虑(7)式的特征根为λ1,2=±iω和λ3,为了得到这个条件,引入
将(18)式代入系统(4)并进行线性部分和非线性部分的分离,可得
其中:
其中O|x1|+|x2|+|x3|4是关于变量(|x1|,|x2|,|x3|)的四阶多项式函数.
通过引入可逆变:
其中,系数
$q_{l_{1} l_{2}}\left(l_{1}, l_{2}=1, \cdots, 3\right) $ 的表达式为:那么系统(19)的标准型可以写为
其中,
式中:多项式
$\widetilde{F}\left(y_{1}, y_{2}, y_{3}\right) $ 的系数为$ \widetilde{m}_{j_{1} j_{2} j_{3}}, \tilde{n}_{j_{1} j_{2} j_{3}}, \tilde{l}_{j_{1} j_{2} j_{3}}$ .基于中心流形理论,利用原点处存在的中心流形WC(0,0,0)对系统(23)降维,即
其中,
通过计算可得:
相应地,系统的动力学性质被限制在中心流形WC(0,0,0)处,联立(25)式,系统(23)可以简化为
其中:
式中:
引入偏导数记号,
下标y1和y2分别表示对第1个和第2个变量求偏导数.
基于(29)式,可得
$ g_{y_{1}}=0, g_{y_{2}}=-\omega \neq 0, p_{y_{1}}=\omega \neq 0, p_{y_{2}}=0$ 和$g_{y_{2}} p_{y_{1}}<0 $ .此外,它能确保系统(28)有纯虚特征根$ \pm i \sqrt{ | g_{y_{2}} p_{y_{1}}} |$ .所以,可以最终确定系统(4)产生Hopf分岔[12]:化简(32)式可得
总结上面的分析,如果条件(17)和(33)同时满足,那么系统(4)在共存平衡点
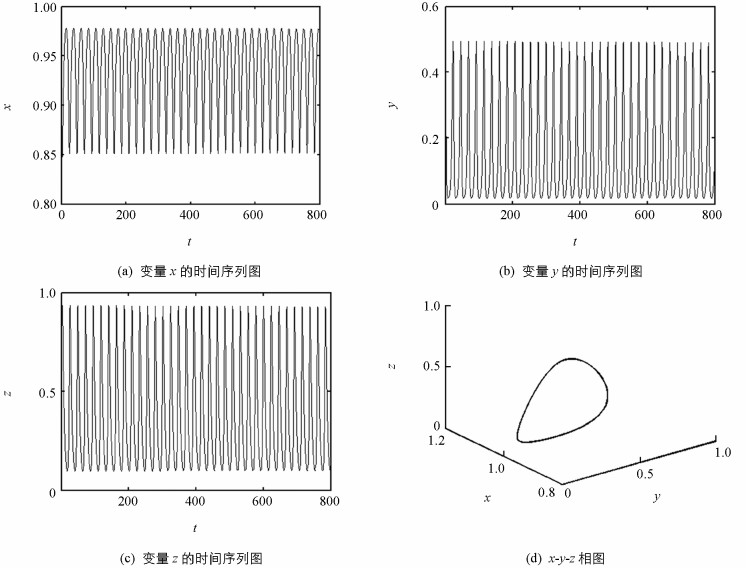
$\left(x_{r_{0}}^{*}, y_{r_{0}}^{*}, z_{r_{0}}^{*}\right) $ 处将产生Hopf分岔.此外,当$ \left.\frac{\mathrm{d} v}{\mathrm{d} r}\right|_{r=r_{0}}<0$ 时:①如果Kr0<0且0<r-r0≪1,那么系统(4)将产生超临界Hopf分岔并形成稳定的周期轨,其半径大约为$\sqrt{\left|\nu_{r_{0}} / K_{r_{0}}\right|} $ ;②如果Kr0>0且0<r-r0≪1,那么系统(4)将产生亚临界Hopf分岔并形成稳定的周期轨,其半径大约为$ \sqrt{\left|\nu_{r_{0}} / K_{r_{0}}\right|}$ .此结果表明3种群食物网系统中可能存在Hopf分岔行为,现举例验证这一结果.选择参数r为分岔参数,其他的参数见(10)式.在此参数条件下,可得系统(4)经历Hopf分岔的临界值r0=3.051 5,同时在分岔临界点处的共存平衡点为E*(0.930 0,0.143 1,0.368 5),相应的特征值为λ1,2=±0.314 963i和λ3=-2.707 03,即具有一对共轭的纯虚根.此外,根据以上的计算结果,可以进一步得到$\left.\frac{\mathrm{d} v}{\mathrm{d} r}\right|_{r=r_{0}}=-0.0105031<0 $ 和最后的Hopf分岔决定值Kr0=-2.421 59<0.由此可知,系统(4)将产生超临界Hopf分岔并形成稳定的周期轨迹.图 2展示了当r=3.3时,食物网系统的动力学行为.相应地,Jacobian矩阵J(E*)对应特征方程的特征根为
可见特征根的实部不全小于零,表明系统(4)是不稳定的.
由Routh-Hurwitz判据,可得:
可见条件Δ1>0,Δ2>0和Δ3>0不能同时满足,这也就意味着系统(4)是不稳定的. 图 2(a)、图 2(b)和图 2(c)反映了随着时间的演化变量x,y,z始终处于震荡状态. 图 2(d)中x-y-z相图明确地表明其轨迹是一个稳定的极限环.
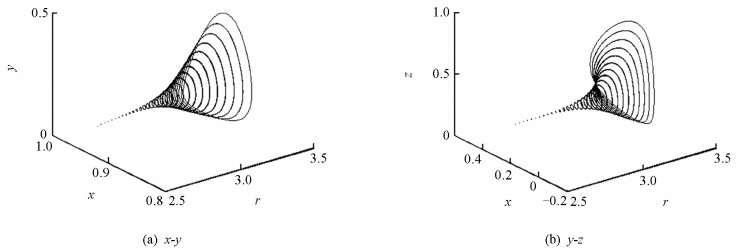
图 3展示了随参数r变化的Hopf分岔图.随着参数r的增大系统(4)的x-y相图和y-z相图由一个稳定点变成一个极限环,这一变化过程充分地显示了Hopf分岔和相应的动力学转变过程.
-
研究了Holling-Ⅱ型三种群食物网系统的Hopf分岔行为.通过Jacobian矩阵、中心流形理论和Hopf分岔理论,讨论了食物网系统产生Hopf分岔的条件.选择恰当的参数,系统能够产生超临界Hopf分岔,即随着分岔参数r的变化,系统的动力学行为由稳定的中心转变成周期轨.



 下载:
下载: