-
混沌同步一直是非线性领域研究热点[1-3].随着分数阶微积分理论的不断完善,整数阶同步方法被推广到分数阶领域,实现了分数阶混沌系统之间的同步[4-5].
在实际中,不同阶数和不同维数的混沌系统的同步问题也引起人们的关注[6-7].目前的研究主流是整数阶与分数阶的同步[8-11].所有的研究可以被概括为两种:①使用Laplace变换,将分数阶转换成整数阶[8-9];②利用追踪器的思想[8, 11].利用追踪器思想是实现不同分数阶数的混沌系统的主流方法[12-14].此外,参数不确定是混沌系统中由于数学建模、噪声等原因而普遍存在的现象,对混沌的同步会产生一定的影响.
滑模控制方法是自动控制领域内一种常用的设计方法[6],其设计与系统参数无关,抗外界干扰能力强.因此,处于滑模运动的系统具有很好的可靠性、鲁棒性,并且能够快速响应,也不需要系统进行在线辨识,物理实现简单[6].目前尚无文章采用滑模方法来研究阶数不同的混沌同步.
本文为实现带有不确定参数的异结构不同阶的混沌系统的广义同步,结合滑模控制和自适应方法,提出自适应同步准则.基于重新构造的受控响应系统的思想,设计整数阶滑模面;再基于追踪器的思想,设计分数阶滑模面.进而采用Lyapunov稳定性理论进行稳定性分析.本文的研究拓展了对于不同阶系统的研究方法,并拓展了滑模变结构控制的研究领域.
全文HTML
-
为了进行稳定性分析,还需要一个必要的引理.
引理1[15] 自治系统
$D_t^q\mathit{\boldsymbol{x}}(<italic>t</italic>) = \mathit{\boldsymbol{Ax}}(<italic>t</italic>),\mathit{\boldsymbol{x}}\left( 0 \right) = {\mathit{\boldsymbol{x}}_0}$ 是渐进稳定的当且仅当其中:
$D_t^q\mathit{\boldsymbol{x}}(<italic>t</italic>)$ 表示x(t)的Caputo分数阶微分;eig(A)计算矩阵A的特征值;arg(z)计算z在空间中的辐角.注 本文没有应用分数阶微分的性质进行求解等问题,因此分数阶微分的定义方式对于本文同步方法的结论没有影响,即结论同样适用于Riemann-Liouville,Grunwald-Letnikov和Weyl的定义方式.
-
驱动和响应系统的数学模型如下:
其中:α,β∈
$\mathbb{R}$ ,x(t),y(t)∈${\mathbb{R}^n}$ ,A,B∈${\mathbb{R}^{n \times n}}$ ,f(x(t)),g(y(t)):${\mathbb{R}_ + } \times {\mathbb{R}^n} \to {\mathbb{R}^n}$ 分别为系统的阶数、状态变量、参数矩阵和非线性项,而Δf(x(t)),Δg(y(t))∈${\mathbb{R}^n}$ 是参数的不确定性,D1(t),D2(t)∈${\mathbb{R}^n}$ 为额外的噪音,u(t)为待设计的控制项.系统的不确定性和扰动通常比较小,则存在常数γ1,γ2,使得
和
令误差为e(t)=y(t)-x(t).只要构造合适的控制器u(t)使得
即说明实现了不同阶系统(2)和(3)间的同步.本文使用两种思想实现了具有不同分数阶数的系统的自适应滑模同步.
-
由于两个分数阶混沌系统的阶数不同,因此不能通过对两个系统做差得到误差系统.重构系统法的主要思想是以原响应系统为主体,结合驱动系统的输出来构造新的受控响应系统[12].
其中
${\mathit{\boldsymbol{N}}(\mathit{\boldsymbol{x}}) = \mathit{\boldsymbol{\dot x}}(t) - D_t^\alpha \mathit{\boldsymbol{x}}(t)}$ .结合驱动系统(2),得到误差系统
假设驱动系统和响应系统的非线性项满足Lipschitz条件,即存在两个Lipschitz常数使得
其中Lf,Lg为两个正常数.
-
其中S(t)=(S1(t),S2(t),…,Sn(t))T,K∈
${\mathbb{R}^{n \times n}}$ .根据滑模具有的性质,当响应系统(4)模动时,满足以下条件
对滑模面(8)求导,有
即
因此需要设计矩阵K使引理1成立,从而实现系统(5)的渐进稳定.
因此令滑模面的达到率为
进而,设计控制器为
其中:r,ρ1,ρ2为非负常数;sgn(·)是符号函数;γ1,γ2是对未知常数γ1,γ2的近似值.控制器(10)满足如下自适应率:
其中k1,k2为非负常数.而对于两个Lipschitz常数的近似值Lf,Lg,其自适应率满足:
其中kf,kg为非负常数.
因此在控制器(10)条件下,误差系统(5)变为
-
定理1 对于误差系统(15),令控制器中的参数为r>0,ρ1>1,ρ2>1,δf>1,δg>1.选择矩阵K,满足
则误差系统是渐进稳定的.
证 构造如下Lyapunov函数
求导可得
结合式(8),(11),(12),(13),(14),(15)得
化简整理得
则误差系统是稳定的.
-
重新构造一个受控响应系统的方法在很多情况下并不方便,而且容易造成额外的误差影响.为此我们考虑在原有的受控响应系统中加入驱动系统的输出信号来讨论两个系统的同步问题.
追踪器方法的主要思想是要求受控响应系统的输出y(t)跟踪驱动系统的输出x(t)[8].由于要实现的是分数阶混沌系统的输出信号的追踪,因此对输出参考信号x(t)采取相应的分数阶微分操作.因此,控制器被设计为
其中U(t)为将要设计的控制器,u(x)是补偿器,且有
则得到分数阶误差系统
-
其中S(t)=(S1(t),S2(t),…,Sn(t))T,K∈
${\mathbb{R}^{n \times n}}$ 控制增益矩阵.相似的,当响应系统(3)模动时,应满足条件
则有
由(21)式可以得到
因此需要设计矩阵K使引理1成立从而实现系统(19)的渐进稳定.
对应的,设计控制器为
其中r,ρ1,ρ2为非负常数,sgn(·)是符号函数.γ1,γ2是对未知常数γ1,γ2的近似值,自适应率其满足(11)和(12).
在控制器(22)的条件下,误差系统(19)变为
-
定理2 对于误差系统(23),控制器中的参数为r>0,ρ1>1,ρ2>1.选择满足引理1条件的矩阵K,则误差系统是渐进稳定的.
证 构造如下Lyapunov函数
求导得
结合式(20),(11),(12),(23)得
化简可得
则可知误差系统是稳定的.
-
当驱动系统和响应系统的非线性项满足Lipschitz条件时,即存在两个Lipschitz常数使得
其中Lf,Lg为两个正常数.
滑模面的设计仍如式(20)所示,设计新的控制器为
其中r,ρ1,ρ2,δf,δg为非负常数,sgn(·)是符号函数.γ1,γ2是对未知常数γ1,γ2的近似值,其自适应率满足(11)和(12),而对于两个Lipschitz常数的近似值Lf,Lg,其自适应率满足(13)和(14).
则误差系统(19)变为
定理3 对于误差系统(25),控制器中的参数为r>0,ρ1>1,ρ2>1,δf>1,δg>1.选择使引理1成立的矩阵K,则误差系统是渐进稳定的.
证 构造如下Lyapunov函数
求导得
结合式(11),(12),(13),(14),(20),(25)得
化简可得
则误差系统是稳定的.
注 在追踪器中设计分数阶微分,在保留原始分数阶驱动系统拓扑结构的基础上,使得控制器可以直接追踪分数阶驱动系统.这样在设计上进行了简化,避免了转换操作可能产生的计算误差.
2.1. 重构系统法
2.1.1. 设计整数阶滑模面
2.1.2. 同步条件
2.2. 追踪器的方法
2.2.1. 设计分数阶滑模面
2.2.2. 同步条件
2.2.3. 进一步延伸
-
选取两个混沌系统进行数值模拟.
选取Chen系统(27)作为驱动系统和Qi系统(28)作为响应系统
其中:
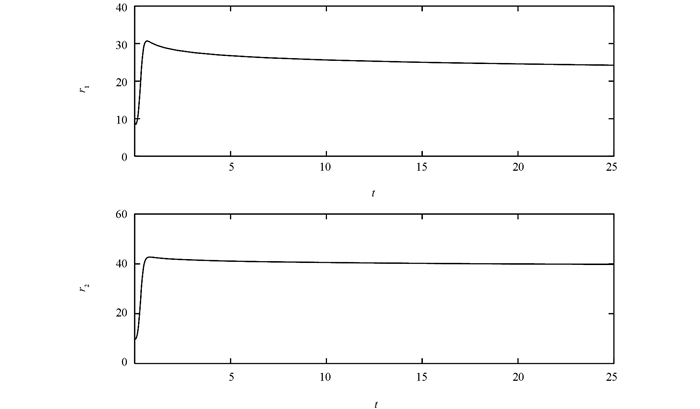
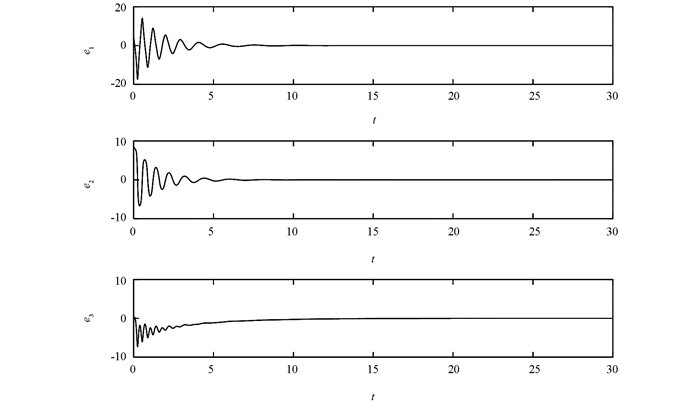
$\mathit{\boldsymbol{A}} = \left[ \begin{array}{l}\ -a\ \ \ a\ \ \ \ 0\\c - a\ \ c\ \ \ \ \ 0\\\ \ \ \ 0\ \ \ \ \ 0 \ -b\end{array} \right],f(\mathit{\boldsymbol{x}}) = \left( \begin{array}{l}0\\ - {\mathit{\boldsymbol{x}}_1}{\mathit{\boldsymbol{x}}_3}\\{\mathit{\boldsymbol{x}}_1}{\mathit{\boldsymbol{x}}_2}\end{array} \right),\mathit{\boldsymbol{B}} = \left[ \begin{array}{l} -{a_1}\ \ {a_1}\ \ \ \ 0\\\ \ {c_1}\ \ \ {d_1}\ \ \ \ 0\\\ \ 0\ \ \ \ \ 0 \ \ -{b_1}\end{array} \right],g(\mathit{\boldsymbol{y}}) = \left( \begin{array}{l}4{\mathit{\boldsymbol{y}}_2}{\mathit{\boldsymbol{y}}_3}\\ - {\mathit{\boldsymbol{y}}_1}{\mathit{\boldsymbol{y}}_3}\\{\mathit{\boldsymbol{y}}_1}{\mathit{\boldsymbol{y}}_2}\end{array} \right)$ ,a=35,b=3,c=28,a1=14,b1=43,c1=-1,d1=16.定理1和定理2只是证明方法的不同,只做一次数值模拟.阶数分别为α=0.95和β=0.98;系统初值为x0=(6,2,4)T和y0=(-6,-6,2)T,常数r=2,ρ1=2,ρ2=2.5.数值模拟结果为图 1和图 2.
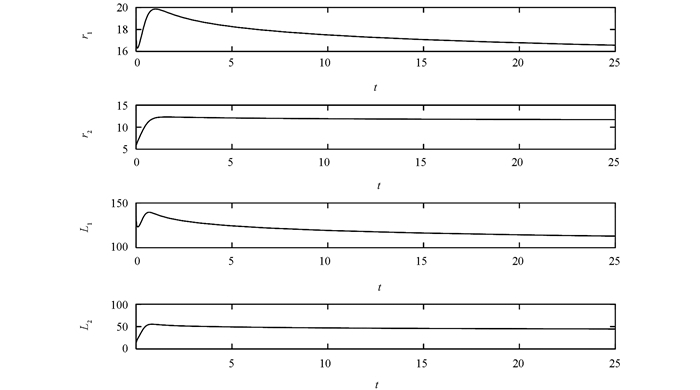
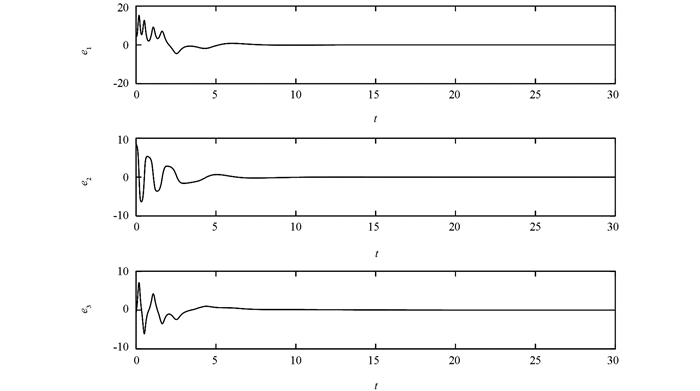
对于定理3,阶数为α=0.95和β=0.98;常数r=2,ρ1=2,ρ2=2,δf=1.8,δg=2;系统初值为x0=(-4,18,-6)T和y0=(2,3,2)T.数值模拟结果为图 3和图 4.在图 3中,r1和r2分别表示系统(27)和(28)中的不确定项,而L1和L2表示未知的Lipschitz常数.
-
本文针对带有不确定参数的不同阶的混沌系统,提出自适应滑模同步准则.采用重构新的受控响应系统和追踪器思想这两种方法,分别构造整数阶和分数阶滑模面来设计自适应控制器.减少计算量的同时避免了建模误差,从而使得系统的同步性更准确.



 下载:
下载: