(1) Density-Graph法原理

Density-Graph法识别城市建成区的原理是根据兴趣点密度等值线在城市与乡村的疏密程度不一，在城市内部兴趣点密度高，密度等值线相对紧密，在乡村区域密度低，等值线相对稀疏. 针对这一属性特征，通过刻画密度与等值线半径增长的变化规律来识别城市与乡村的界线. 等值线所围成的闭合曲线面积为S_d，理论半径为$\sqrt {{S_d}} $，以密度值d为横坐标，理论半径增量Δ$\sqrt {{S_d}} $为纵坐标做图，即Density-Graph图. 在理想情况下，城市内部密度等值线是均匀扩散的，其理论半径增量是一个常数，求导可得：

然而实际的城市内部空间结构具有复杂性，理论半径增量是不完全均匀的，因而有：

当理论半径增量的导数大于0时说明曲线向外发散；当导数小于0时说明曲线收缩. 由于城市内部的复杂性，以及城市多中心的存在，在城市建成区范围内理论半径增量是在一定范围内波动的，将这个波动范围设定为容许值r，当导数超过设定的容许值r，且曲线变化趋势不可逆时，认定拐点出现，即：

以此时的兴趣点密度d分割密度表面，即可得到城市建成区.

(2) 核密度分析

核密度方法是通过核密度函数估计点要素在周围邻域内的密度^[19]，是高质量的密度估计方法.

式中，P_i为估计点i的估计密度值；h为研究对象j点的周围规则邻域宽度，即带宽；n为带宽内样本点的数量；D_ij为待估点与研究对象j的距离；W_j为研究对象的权重. 带宽h对核密度分析结果产生影响，需要根据空间点的分布状况以及研究问题的实际情况确定. 研究为避免人为主观设定，使用“Silverman经验规则”确定带宽. 该规则依靠点数据自身的空间分布确定搜寻半径，确定整个事件点的平均中心，计算平均中心到各个事件点的距离，取这些距离的中位数D_m，并计算事件点的标准距离SD^[9]，即：

式中，SD为标准距离；D_m为中值距离.

(1) 城市扩张曲线

Tannier认为城市内部空间形态类似于白色街道线条对黑色建筑方块的切割，随着白色线条宽度的减小，黑色方块数量减少^[12](图 1). 白色线条的宽度与黑色方块的数量遵循幂函数规律，即以城市建筑进行扩张，随着扩张半径的增大，城市建筑彼此融合直至形成一个斑块，扩张半径R与斑块集群数量N符合幂律关系，集群数量与扩张半径的关系曲线为城市扩张曲线.

式中，N为集群数量；a为常数；R为扩张半径；D为分维数. 对等式两边取对数得到双对数曲线函数，可见分形理论上的双对数曲线是以D为斜率的直线.

(2) 城市扩张曲线曲率变点

然而城市只具有类似于前分形的特征，即只在某个范围内扩张半径与集群数量具有相同的变化规律. 因此双对数曲线中的斜率D并不是一个常数，而是一个变化量，对双对数曲线进行拟合，其偏离理论直线最大点就是城乡分界拐点. 参考相关研究^{[12-13, 20]}，引入城市扩张曲率，来测度双对数曲线偏离直线的程度. 曲率是表明曲线偏离直线程度的指数，用其定量测量双对数曲线拐点，具有客观性，曲率计算公式如下：

式中$\ddot y$，为曲线二阶导数，$\dot y$为曲线一阶导数. 在有效的扩张半径内，曲率绝对值最大时得到城乡分界拐点. 由于矢量建筑数据获取困难，参考学者^[13]的方法，以道路交叉点代替矢量建筑进行扩张.

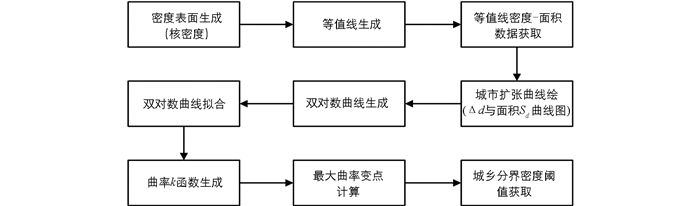
基于Density-Graph法与城市扩张曲线法，研究提出一种以兴趣点密度中心代替地理实体构建扩张体，以密度搜索为扩张半径进行扩张，通过密度与对应等值线面积的变化规律来确定城市建成区的方法(图 2). 该方法主要包括3个步骤：最小扩张单元的构建、城市扩张曲线绘制、城乡分界阈值识别.

城市是兴趣点集聚的区域，具有以兴趣点密度中心向四周发散，随着密度值的减小，城市覆盖面积逐渐变大，在城乡交界处出现突变的特征. 因此可将其城市空间抽象为以密度中心为中心的同心圆，以密度中心向外扩张，随着密度值的减少，等值线围成的面积增大，显然在城市内部密度值d与对应等值线面积S_d之间存在数学联系.

Density-Graph法以及相关研究^{[1, 9, 18]}已说明与验证了在城市内部兴趣点密度以及车辆轨迹点密度等值线围绕密度中心接近均匀分布，即使出现小范围的波动也可将其视为均匀. 则由公式(1)与(2)可推出，密度值d与等值线理论半径S_d存在以下关系：

其中，$\sqrt {{S_d}} $为密度中心对应的理论半径值；d_max为密度中心对应的密度值；a₁为常数. 在密度中心理论半径很小，接近于0，则公式(9)可变为：

为简化公式，令：

则在城市内部，等值线面积S_d与密度值变化量Δd关系可近似为：

式中，S_d为等值线所围成的面积；a为常数；Δd为密度变化量；D为分维数. 显然，S_d与Δd遵循幂律关系，符合分形理论规律，可用城市扩张曲线描述其关系. 类似于Tannier将城市空间抽象为白色街道线条对黑色建筑方块的切割，该关系只在城市内部成立. 双对数曲线是表示物体分形测量结果的常用方式^[21]，因此其也适合展示在城乡区域由于密度值的不同造成的密度值面积产生分形的结果. 同样的也可通过多项式对双曲线进行估算，进而求出最大曲率变点，计算出密度阈值，提取城市建成区. 兴趣点密度与城市扩张曲线结合法提取城市建成区流程如图 3.

研究选择重庆市中心城区二环区域为研究对象，重庆市中心城区原为重庆市主城区，2020年5月重庆主城区由9区扩容到21区，原主城区变为中心城区，其城市建成区主要分布在二环区域内. 其城市中心为明显的多中心结构^[22]，相较于单中心、双中心等结构城市空间结构更复杂，以其为研究区能够保证识别方法在其他研究区的适用性.

研究数据包括2019年重庆市中心城区全类别兴趣点数据、2018年土地利用现状图. 全类别兴趣点数据量为610 286个，通过高德地图API采集. 数据进行了去重与坐标纠偏处理. 2018年土地利用现状图由中国科学院资源环境中心下载，该数据基于Landsat 8遥感影像，通过人工目视解译生成，用于与识别结果比较，以验证识别方法精度.

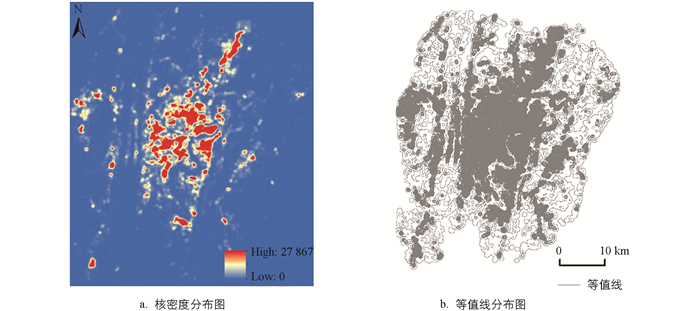
采用“Silverman经验规则”确定核密度带宽为796.83m，通过Arcgis核密度分析工具生成兴趣点密度面，如图 4(a)所示，兴趣点密度分布与城市空间分布接近，核密度区间在0~27867之间. 生成的栅格面是平滑的表面，为获得更多的数据反映密度与等值线面积的关系，通过Arcgis提取等值线工具，设置等值间距为10提取等值线，如图 4(b)，等值线分布与密度中心相对应.

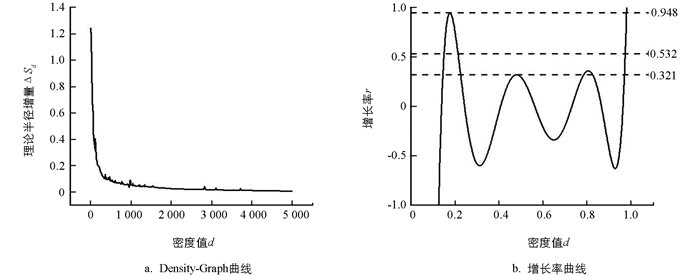
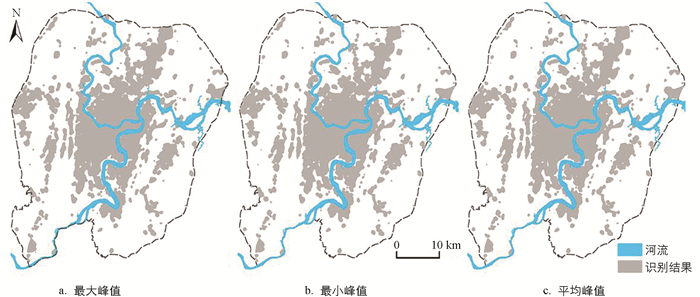
以密度值d为横轴，理论半径增量Δ$\sqrt {{S_d}} $为纵轴绘制Density-Graph曲线，如图 5(a). 随着密度值d的降低，曲线的趋势呈接近水平偶有波动的形态，随着密度值越来越低，曲线逐渐上升，直至在某个点急剧上升. 由曲线的变化趋势，可以判断在城市内部密度等值线分布均匀，理论半径增量趋于稳定，由于城市内部结构，会出现某种波动，但总体上趋于平稳，在靠近城乡边界处，曲线增长幅度开始加大，直至超过城市内部结构容许值时达到城乡分界拐点.

对密度值与理论半径增量进行无量纲处理，对无量纲化的Density-Graph曲线进行拟合，为保证拟合精度，仅选取0~500密度值与对应的理论半径增量进行拟合(根据Density-Graph图密度阈值不可能大于500)，拟合R²在0.96以上，对拟合曲线求导，求出理论半径增长率曲线如图 5(b). 与Density-Graph曲线变化对应，随着密度的变化增长率先是呈波动状态，随后在拐点处出现不可逆的下降趋势. 由增长率曲线可看出，研究区城市内部结构的复杂，波动性强，增长率的波动远大于学者^[1]提出的5%的容许值，因此针对研究区实际情况，分别选择波动状态下的最小峰值、最大峰值以及所有峰值的平均值作为容许值，当理论半径增长率大于容许值且呈现不可逆的趋势时，提取密度阈值点(表 1).

根据识别的阈值点提取城市建成区，结果如图 6. 在不同容许值下提取的最佳密度阈值有差异，识别结果也有差异，虽然此处由于在拐点之后增长率几乎呈直线下降，不同容许值提取的密度阈值差异不大，但可判断容许值对密度阈值的影响与增长率的变化幅度有关. 因此Density-Graph法识别城市建成区结果受容许值影响，在不同区域的城市需要设定不同的容许值，如何确定最优容许值还需研究.

道路交叉节点可以反映人类活动范围和空间形态特征^[23]，即使最小的城镇也至少有一个道路交叉节点^[24]，因此以道路交叉点代替矢量建筑进行扩张具有可行性. 基于Arcgis 10.5平台将国道、省道、县道、乡道以及城市四级道路合并为一个图层，将所有道路线段进行合并处理，避免同一条道路出现断点，然后建立拓扑关系，在交点处打断线，通过建立网络数据集以及空间链接获取连接线段为2以上的点，即可获得道路交叉点. 借助Arcpy模块编写程序实现道路交叉点以5 m为步长，从5~1 000 m的扩张(缓冲分析)，并统计各个扩张距离下集群体的数量.

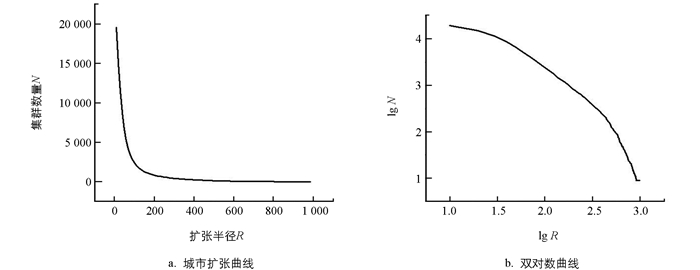
以扩张半径为横轴，集群数量为纵轴绘制城市扩张曲线，如图 7(a)，随着扩张半径的增加集群数量在不断减少. 对扩张半径与集群体取对数，绘制双对数曲线，如图 7(b)，可见双曲线不是直线具有明显的分形特征.

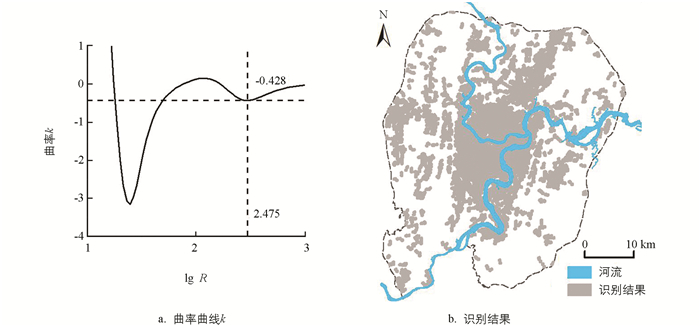
对双对数曲线进行拟合，拟合R²为0.99，代入式(6)，求出曲率函数. 通过曲率函数绘制曲率曲线如图 8(a)，由曲率曲线可看出，出现了多个曲率极值点，由实际城市道路交叉点距离可判断最佳扩张半径不可能小到几十米，也不可能大到上千米. 因此具有实际意义的lgR范围为[1.5~3]，在此区间以绝对值最大的曲率极值-0.428，对应的搜索半径298.37 m提取城市建成区，结果如图 8(b). 相关学者^{[8, 12-13]}在识别出最佳扩张半径之后，选择面积最大的集群体作为城市建成区. 然而，在不同的研究区中，“一城多区” “一城多镇”城市空间形态很常见，研究区两种城市空间形态都具备，单以最大集群面积的集群体代表城市建成区显然不符实际；另外，为直观地说明最小扩张单元对最后识别结果的影响，研究以所有集群体作为最后的识别结果.

由识别结果可以看出，在主要的城市区域，道路交叉点密度大，分布均匀，随着搜索半径的增加，道路交叉点逐渐融合，识别效果较好. 在道路交叉点密度小的区域，点与点之间距离较远，在识别出的最佳扩张半径内无法融合，因此形成了一个个独立的集群体. 这种现象有两种原因：一种是这些独立的集群体同样是城市建成区，但山地城市受地形影响，城市建成区结构较平原城市复杂，同样是城市建成区，道路交叉节点具有区域差异性，在全局最佳搜索半径内并未融合，使识别结果产生误差；另一种是这些独立的集群体并不是城市建成区，而仅仅是一个道路交叉路口，作为最小的扩张单元最后以独立的集群体存在.

由上述分析可得，以道路交叉点或矢量建筑等地理实体进行邻域扩张，绘制的城市扩张曲线通过曲率变点，能客观地识别城乡分界拐点，但其识别结果受最小扩张单元影响；同时在山地城市，由于城市结构差异较大，以地理实体数据作为最小扩张单元识别城市建成区适用性没有在平原城市好. 因此基于地理实体数据的城市扩张曲线识别方法更适用于城市形态分布均匀的区域，且最小扩张单元必须是城市建成区的一部分，对数据准确性有着严格要求.

由于识别结果精度的判断受多种因素影响，在此不对两种方法最终的识别精度进行比较，仅针对两种识别方法阈值确定的客观性、识别结果的确定性进行比较. 确定性指识别结果是否一定属于城市建成区.

Density-Graph法识别阈值之前需要确定容许值，容许值的确定需要考虑城市空间结构的复杂性，当前仍简单的依靠设定的经验值确定，存在主观性；城市扩张曲线通过最大曲率变点识别城市建成区阈值，在有效的区间内，最大曲率变点代表了曲线偏离直线的最大点，完全通过曲线形态识别，显然客观性更好.

Density-Graph通过密度分析进行筛选，小密度区域直接被剔除，识别结果中密度中心一定属于城市建成区，受阈值的准确性影响，在边界处，识别结果可能偏大或偏小；城市扩张曲线以道路交叉点或矢量建筑等地理实体进行扩张，然而，独立的道路交叉点或矢量建筑在城市与乡村是相似的，不论确定的扩张半径是多少，乡村地理实体的扩张体也被包含在识别结果中，造成了识别结果的偏大，显然在确定性上Density-Graph更好.

在客观性与确定性上两种方法结合可以实现互补，继承优点，弥补不足. 兴趣点密度等值线在反映城市属性的同时具有形态学上的规律，使两种方法结合成为可能.

兴趣点密度中心与城市空间分布一致，可以判断兴趣点密度中心一定属于城市建成区. 不同于以地理实体进行扩张，地理实体仅仅考虑了城市在某方面的几何形态，没有考虑城市要素集聚的属性特征，因此某些具有与城市实体形态相近却不属于城市建成区的区域会被识别，比如上述的乡村道路交叉节点及城市周边的工矿厂房. 以核密度生成的兴趣点密度中心是城市实体在空间上集聚的高值区域，其形成的等值线也具有几何分形特征，因此以兴趣点密度中心等值线构建最小扩张单元能够弥补以矢量建筑或道路交叉节点数据的缺陷. 研究构建以兴趣点密度中心为扩张体，以密度搜索为扩张半径的最小扩张单元，从密度最大的密度中心开始扩张，随着密度值的减小，集群面积不断增加，直至密度减小到最低值，面积不再增加，停止扩张.

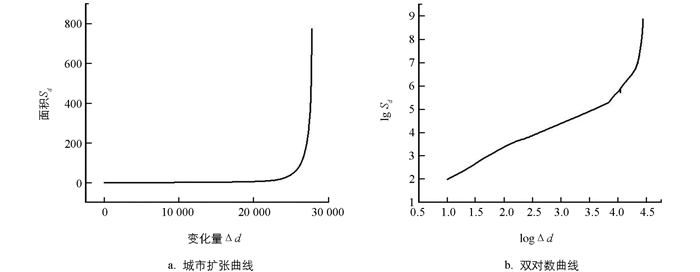
借助Arcpy模块编写程序，统计每一条密度等值线所围成的面积. 以密度变化量Δd(d_max-d)为横轴，集群面积S_d为纵轴，绘制城市扩张曲线；对两边取对数，绘制双对数曲线函数(图 9).

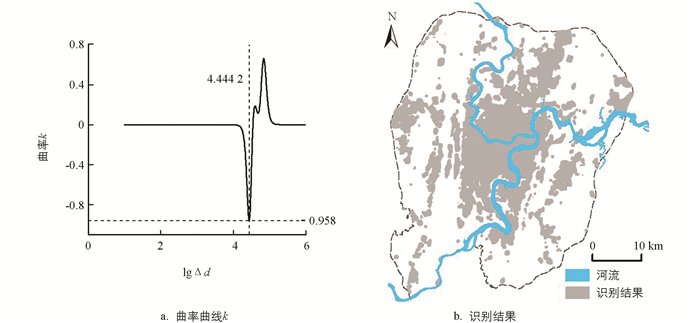
与道路交叉点的城市扩张曲线相似，随着密度变化量的增加集群面积在不断增加，曲线与幂函数曲线相近，双对数曲线不是直线形状，有明显的分形结构，因此在理论上可以找到最大曲率变点. 对双对数曲线进行拟合，拟合R²在0.99以上，求出曲率函数，并绘制曲率函数曲线，如图 10(a).

得到城市扩张曲线对应的最大曲率值绝对值为-0.958，对应的兴趣点密度值d为50.063. 以密度阈值提取城市建成区边界得到研究区城市建成区面积为659.82 km². 识别结果显示[图 10(b)]，研究区城市建成区分布特征显示为“一主区、多片区、多点”的空间分布特征，“一主区”指中心城区中部连片的城市建成区、“多片区”指连片区以外的北碚区、沙坪坝区、巴南区等区县规模离主区较远的城市建成区，“多点”指的是在城市建成区周边的城镇建成区.

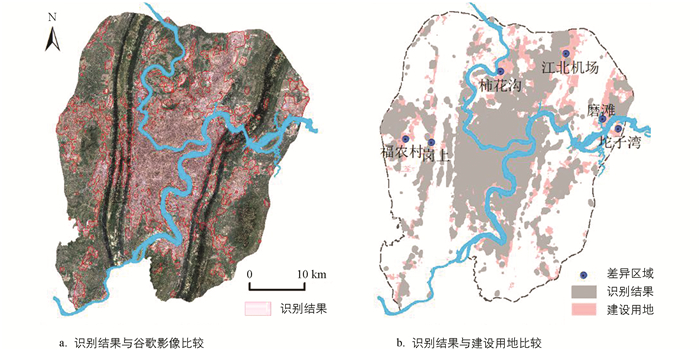
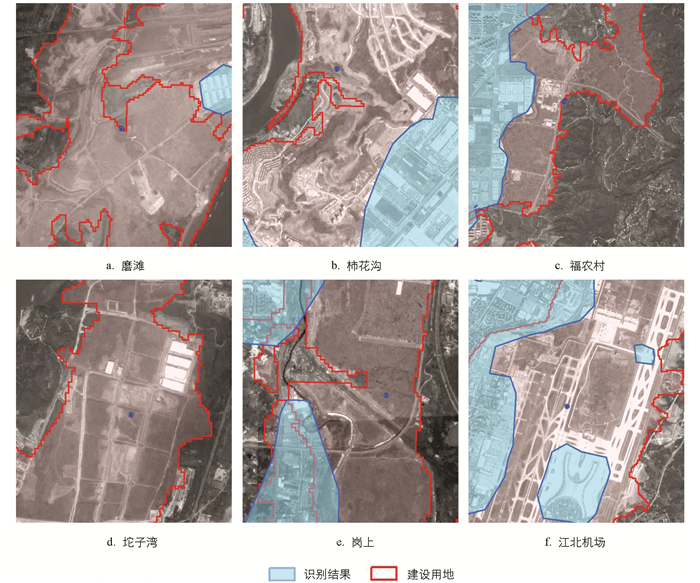
为验证识别结果的精确程度，参考相关学者^{[18, 25-26]}研究结果，使用面积精度与空间重叠度两个指标进行精度检验. 面积精度是指用识别结果与现状真值比较得到面积上的精确程度. 空间重叠度是指用识别结果与现状真值叠加，获得识别结果在空间分布上的精确程度. 由于实际建成区数据难以获得，以土地利用现状中城镇及其他建设用地面积758.84 km²为真值，得到面积精度为86.95%，空间重叠度为89.63%，实际建成区面积要小于现状城镇及其他建设用地面积，因此面积精度应在86.95%以上. 将识别结果与谷歌影像以及2018年二环区域土地利用现状中城镇及其他建设用地叠合(图 11). 识别的城市建成区与城镇及其他建设用地空间分布基本相符，有部分区域识别结果与土地利用现状有较大差异，这些差异有两种原因：一种是该用地属于在建区域，尚未建成，兴趣点覆盖密度小，在属性上与城市建成区概念不符，例如渝北区的鱼嘴镇磨滩区域图 12(a)、悦来街道柿花沟区域图 12(b)、沙坪坝区曾家镇福农村区域图 12(c)、江北区的广阳镇坨子湾区域图 12(d)以及沙坪坝区西永镇的岗上区域图 12(e)；另外一种是由于兴趣点是地理实体在空间上的抽象点，无论空间上面积多大的实体都会抽象为一个点，因此在大型交通运输用地、工厂、厂房集聚的大的区域虽然建筑密度大，然而抽象为兴趣点时仅有少量的兴趣点，从而造成识别误差. 例如渝北区的江北国际机场为大型交通运输用地图 12(f)，识别结果仅覆盖了其中小部分，对于机场跑道等并未覆盖，再次说明以兴趣点密度方法识别更注重城市要素集聚属性特征.

(1) 研究比较了基于城市属性的Density-Graph法与基于城市形态的城市扩张曲线法两种城市建成区识别方法，两种方法各有优点与不足. 在识别效果上Density-Graph方法通过密度识别，能够将城市属性在空间上反映出来，即城市是各类要素在空间上的聚合体，排除了少数的兴趣点对识别结果的影响，但其受容许值估计的主观性影响，在阈值识别上依然带有一定主观性. 城市扩张曲线方法基于城市形态的自相似性与分形理论，通过最大曲率变点，能够客观地识别阈值，但识别结果受最小扩张单元的影响，不管阈值是多少，最小扩张单元必然会被识别为城市建成区，因此该方法要求最小扩张单元能够完全代表城市建成区；另外，由于地形导致的城市空间的复杂性，基于该方法使用矢量地理实体数据识别山地城市建成区，适用性不高.

(2) 结合Density-Graph方法与城市扩张曲线方法，研究提出一种新的城市建成区识别方法. 以兴趣点密度中心等值线代替矢量建筑或道路交叉点等地理实体数据构建最小扩张单元，绘制城市扩张曲线，通过最大曲率变点识别城市建成区. 相较于城市扩张曲线法，该方法以代表实际地物的抽象点POI构建最小扩张单元，能够弥补以地理实体数据扩张时只注重城市形态而忽视城市属性的缺点. 相较于Density-Graph法，该方法同样是根据城市内部与乡村POI密度的差异，来区分城市建成区；不同的是，在识别边界阈值时借用了更加定量化的城市扩张曲线中的最大曲率变点，不用考虑设置容许值，避免了主观判断过程，能够较为客观与准确地确定城乡分界阈值. 两种方法的结合，在一定程度上继承了两种方法的优点，互补了两种方法的不足. 通过实证研究，该方法识别面积精度为86.95%，空间重叠度为89.63%，识别结果具有准确性，该方法可为城市建成区识别提供新思路.

(3) 考虑到地理实体抽象为兴趣点时的同质性，对特殊类别的兴趣点赋予权重，使得兴趣点密度在反映城市属性的同时，在一定程度上能够反映其在空间上的规模，从而弥补在某些大型建筑抽象为兴趣点时密度较小的现象，可作为深入层次的研究. 另外，核密度表面的生成在一定程度上影响着识别结果，通过提前使用最终结果进行环节检验和参数校准，以确定生成密度表面的最佳带宽需要进一步研究. 相较于遥感影像通过地物的反射光谱解译城市建成区，研究所采用方法是基于城市要素集聚属性，一个是基于城市形态，一个是基于城市属性，两者的识别目标为同一个，识别结果可互相验证，因此对于城市内部小范围的非城市建设用地，可通过遥感影像解译后与识别结果综合确定城市建成区，探寻多源数据融合的城市建成区识别方法是今后的研究趋势.