-
开放科学(资源服务)标志码(OSID):

-
在现代生活中,电能作为一种不可或缺的能源,直接影响着我们的生产与生活,所以,高压线路的安全问题逐渐引起了人们的重视. 过去的电力巡检工作往往是由人来完成的,但是存在着安全风险大、工作效率低等问题,而电力巡检机器人可以替代人来完成这种工作.
电力巡检机器人是一种具有强耦合性的欠驱动非线性系统[1-3],在过去的几十年中,人们对于强耦合非线性系统已经进行了大量的研究[4-6]. 欠驱动系统与全驱动系统相比,其输入个数要少于控制量的个数,这为欠驱动系统的控制带来了很大挑战. 但欠驱动系统在节约能量、降低造价、减轻质量、增强系统灵活度等方面都较全驱动系统有一定的优越性. 目前,关于电力巡检机器人运行姿态的研究较少[6-8],于是提出了增益调度动态面控制来控制电力巡检机器人的运行姿态[6],提出了基于增益调度的反演控制来控制电力巡检机器人[7]. 但是在文献[6-7]中,被控对象为电力巡检机器人的线性化模型,而这与工业实际不符,所以,本文将针对电力巡检机器人的非线性模型来展开研究.
滑模控制,也被称为变结构控制,它的特点就在于在动态运动的过程中,其结构可以根据被控对象的状态而产生有目的的变化,进而能够完成整个控制过程,获得更好的控制效果. 滑模控制作为非线性控制的一种有效方法,在实际工程中也得到了广泛的应用,如电机控制、机器人控制、飞行器控制等[9-16].
在滑模控制中,一般会先完成滑模面的设计,然后根据滑膜到达条件完成滑模控制律的求导. 但传统的滑模控制采用的一般是线性滑模面,而线性滑模面在实际应用中也可能存在一定的问题. 一是抖振问题,这是在滑模控制中十分不希望看到的,于是提出了使用趋近律来改善滑模控制中的抖振问题[5],取得了良好的控制效果. 同时,与一些智能控制方法如自适应控制、模糊控制等的结合也可以改善抖振问题[17-20]. 二是收敛问题,传统的线性滑模控制可能会导致其稳态误差不能在有限时间内收敛至零,而终端滑模控制的提出可以有效地解决这一问题[21-23]. 但在终端滑模控制中,有可能会存在控制律的奇异性问题,即系统状态接近零时,控制律中状态负指数项会导致控制量趋向于无穷大,产生奇异点,而非奇异终端滑模控制的提出解决了这一问题.
本文通过使用终端滑模控制以及非奇异终端滑模控制来控制电力巡检机器人非线性模型的运行姿态.
全文HTML
-
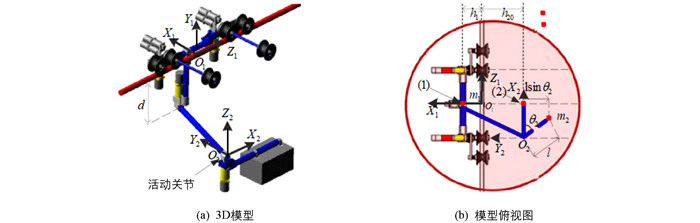
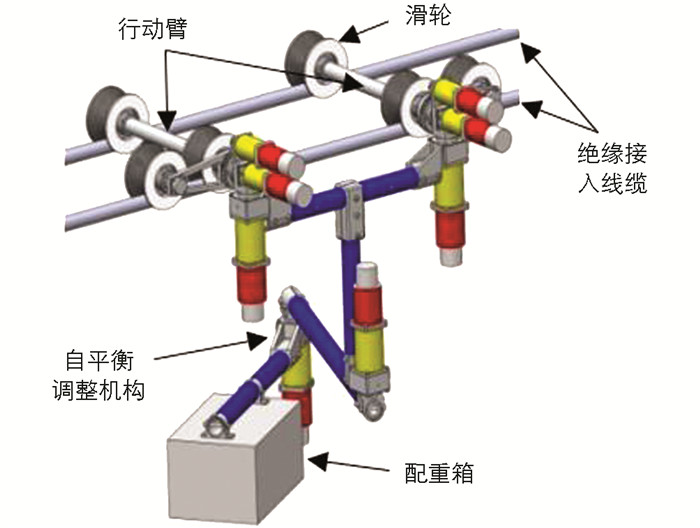
本节将介绍电力巡检机器人的动力学模型,其线载模型如图 1所示,其平衡调整参数如图 2所示. 本节主要参考文献[6-8]. 定义状态变量如下:
其中,θ1是机器人的旋转角,而θ2是活动关节的转动角度.
$ {\dot \theta _1}和{\dot \theta _1}$ 分别是θ1和θ2的角速度.电力巡检机器人的状态方程为
其中m1=63 kg,m2=27 kg,h1=0.18 m,h20=0.42 m,l=d=0.5 m.
其线性化方程为
式(3)又可简化表示为
其中
其中
在式(3)中,x=[x1,x2,x3,x4]T为其状态向量,u为控制输入. 从状态方程中可以看出,电力巡检机器人是一个1输入4输出的强耦合非线性系统,因而对电力巡检机器人的研究是十分有必要的. 传统的滑模控制针对的一般为1输入2输出的非线性系统,而针对电力巡检机器人的欠驱动特性,本文将使用复合滑模面函数来完成控制律的求解.
-
基于第1节中的电力巡检机器人模型,本节将会对终端滑模控制器的设计进行阐述. 基于终端滑模控制方法的思想[21-23],定义终端滑模面函数为
其中,c1,c2为常数,β1,β2为正常数,同时,p1,q1,p2,q2为奇数,且pi>qi>0(i=1,2). 对式(8)求导可得
为了减少滑模控制中可能存在的抖振问题,考虑使用指数趋近律如下:
根据式(9)和式(10),并将式(3)中
${\dot x_n}$ 带入,可得终端滑模控制律为现有的终端滑模控制器的设计方法存在控制奇异问题,即当系统处于状态空间的某个特定子空间时,终端滑模控制器的输出信号可能出现无穷大的情况. 对于终端滑模的控制奇异性问题,现有的一种解决方法是在终端滑模和线性滑模之间进行切换,或者令系统轨迹运动到一个预先指定的保证终端滑模控制非奇异的区域,然而这些方法都是间接的[24-27],而非奇异终端滑模控制的提出,可直接从滑模设计方面解决上述问题.
-
本节将会对非奇异终端滑模控制器的设计进行说明. 基于非奇异终端滑模控制方法的思想[24-25],定义非奇异终端滑模面函数为
其中,d1,d2为常数,γ1,γ2为正常数,并且,m1,n1,m2,n2为奇数,对公式(12)求导可得
为了减少滑模控制中可能存在的抖振问题,加入指数趋近律如下:
根据式(12)和式(13),并将式(3)中
${\dot x_n}$ 带入,可得非奇异终端滑模控制律为
2.1. 终端滑模控制器设计
2.2. 非奇异终端滑模控制器设计
-
本节将会使用终端滑模控制器(TSMC)与非奇异终端滑模控制器(NTSMC)完成电力巡检机器人非线性模型的运行姿态控制. 在终端滑模控制律式(11)中,c1=2.3,c2=4.5,β1=2,β2=8,q1=3,p1=5,q2=11,p2=13. 非奇异终端滑模控制律式(15)中d1=2,d1=4,γ1=2,γ2=0.5,m1=13,n1=15,m2=11,n2=13,且令ε1=ε2=k1=k2=1. 为了更好地对比不同方法的控制效果,考虑使用以下性能指标评价函数:
1) 方差的积分(ISE)
2) 误差绝对值的积分(IAE)
3) 时间乘以误差绝对值的积分(ITAE)
为了更好地对比两种控制器的控制效果,本文考虑了在两种情况下进行仿真.
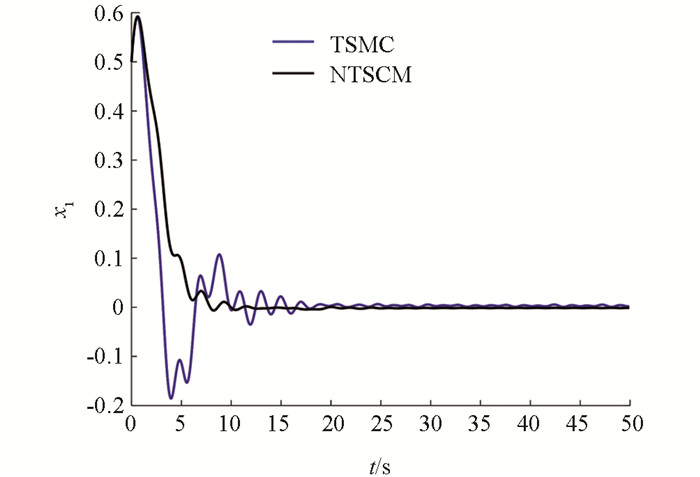
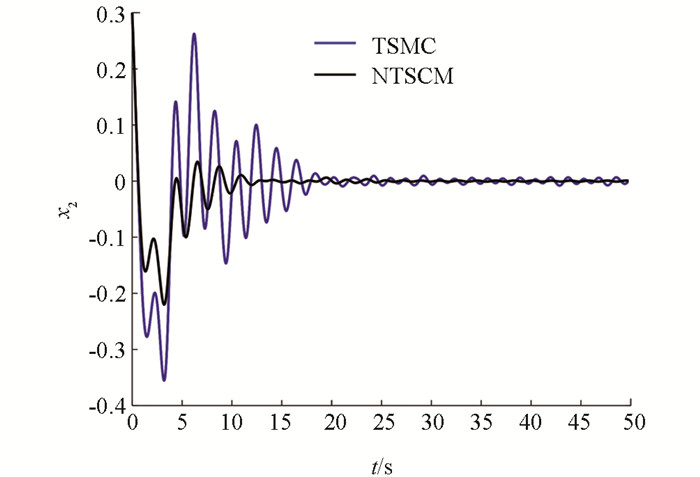
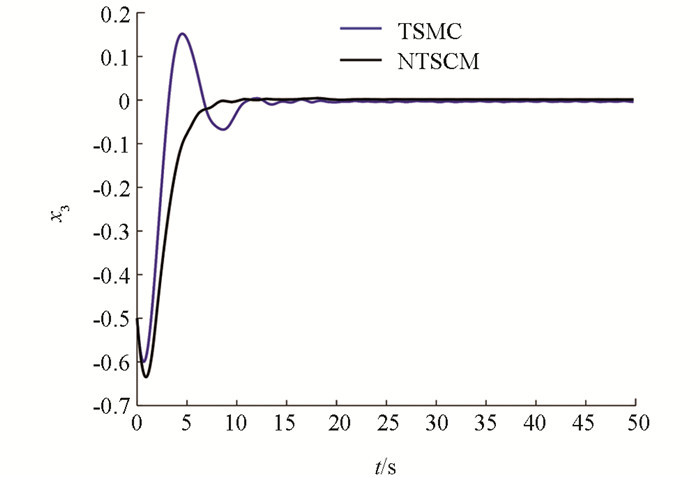
情况1:无外界干扰情况,其仿真结果如图 3-图 6所示,其性能指标值如表 1-表 3所示.
通过图 3-图 6可知,在经过有限时间后,终端滑模控制器与非奇异终端滑模控制器均可以完成电力巡检机器人的平衡控制,但非奇异终端滑模控制器的调节时间要快于终端滑模控制器,并且其超调也要小于终端滑模控制器. 同时可以看出,终端滑模控制器在到达平衡位置之后,还会在平衡位置附近产生小幅的抖振.
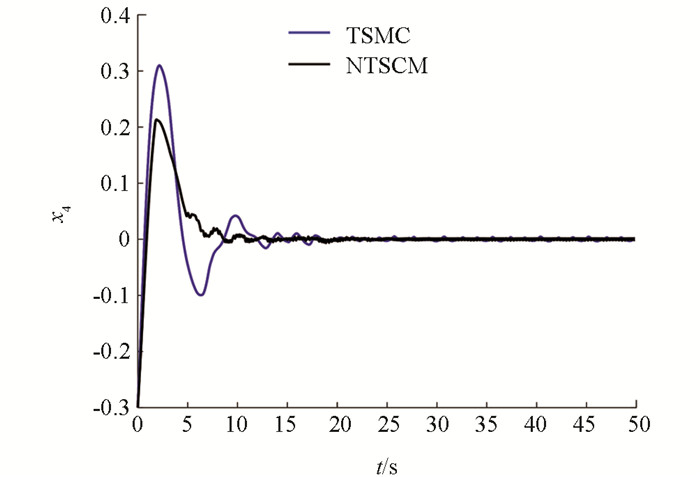
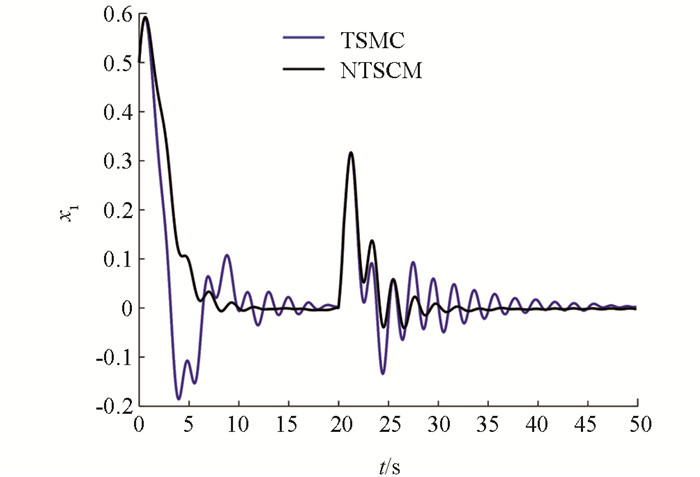
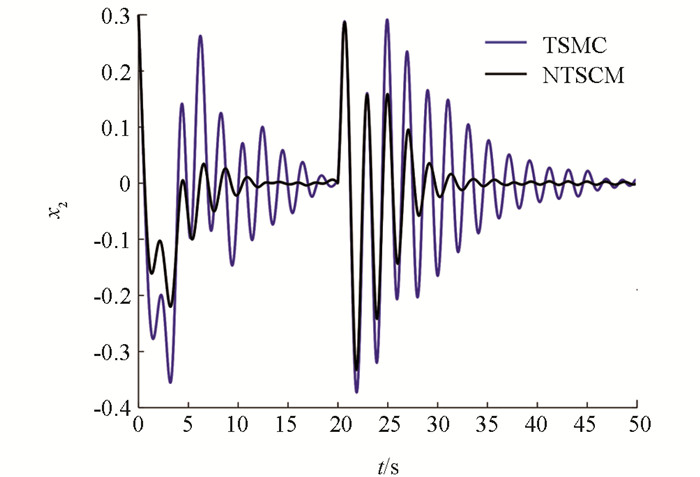
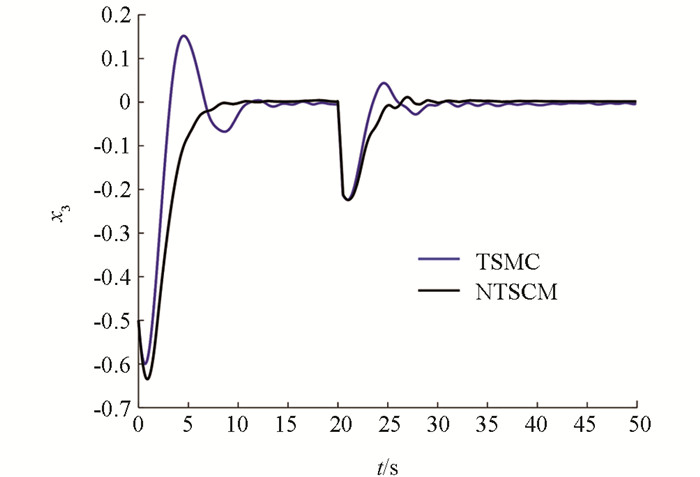
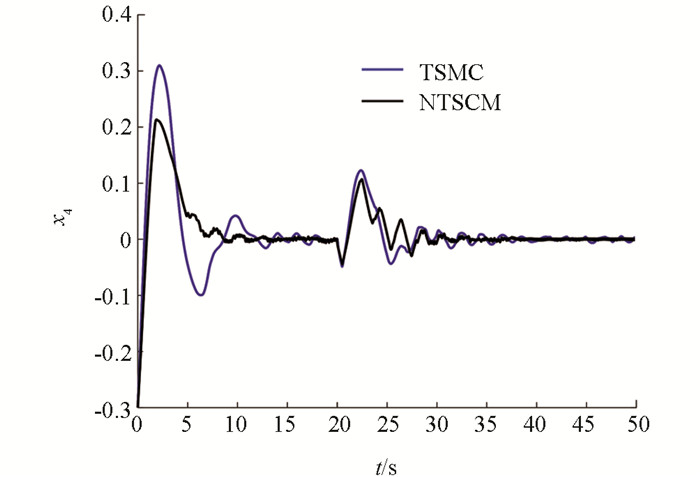
情况2:在第20s时,分别在x1,x2,x3,x4上添加幅值为0.4,0.45,-0.75,-0.3的瞬时冲击扰动,其仿真结果如图 7-图 10所示,其性能指标值如表 4-表 6所示.
通过图 7-图 10可知,当在4个状态上加入不同幅值的瞬时冲击扰动后,两种控制器都能够在一段时间后使电力巡检机器人回归平衡状态,但非奇异终端滑模控制器的调节时间要明显少于终端滑模控制器.
-
电力巡检机器人是一种典型的非线性欠驱动系统,本文使用了终端滑模控制器与非奇异终端滑模控制器来控制其非线性模型,进而完成运行姿态控制. 对于其欠驱动特性,本文将传统的对于1输入2输出系统的终端滑模面设计方法拓展到了1输入4输出的系统. 为了解决抖振问题,本文使用了趋近律,最终设计出了终端滑模控制器与非奇异终端滑模控制器,并将其用于控制电力巡检机器人的非线性模型,使其能够保持良好的运行姿态. 通过仿真结果,可以得到以下结论.
1) 两种控制器均可以完成电力巡检机器人非线性模型的平衡控制,但相比较于终端滑模控制器,非奇异终端滑模控制器的调节时间更短,控制效果更优.
2) 当加入瞬时冲击扰动时,两种控制器均能够使电力巡检机器人经过一段时间的调整后,回归平衡状态. 但通过仿真结果以及性能指标参数可以看出,相比较于终端滑模控制方法,非奇异终端滑模控制的调节速度要更快,这与先前的结论是一致的.
如何减轻滑模控制中存在的抖振问题一直是滑模控制的热点问题,与智能控制系统如模糊控制、神经网络等结合进行研究将会成为我们未来的研究方向.



 下载:
下载: