考虑如下二维非稳态对流扩散方程：

初始条件：

边界条件：

其中：Ω∈[a₁，a₂]×[b₁，b₂]为${\mathbb{R} ^2}$上的矩形区域，∂Ω为Ω的边界，u(x，y，t)为待求未知量，p(x，y，t)，q(x，y，t)分别为x，y方向的对流项系数，α为扩散项系数(常数)，f(x，y，t)为源项，且p(x，y，t)，q(x，y，t)，f(x，y，t)，g(x，y)，s(x，y，t)均为已知函数.

为了不失一般性，将计算区域Ω进行均匀网格剖分，x方向剖分为a₁=x₀，x₁，x₂，…，x_Nx=a₂，y方向剖分为b₁=y₀，y₁，y₂，…，y_Ny=b₂，定义空间步长为h_x=x_i-x_i-1，1≤i≤N_x，h_y=y_j-y_j-1，1≤j≤N_y，以τ表示时间步长， t_n=nτ，0≤n≤M. u_i，jⁿ表示u(x，y，t)在点(x_i，y_j，t_n)处的离散值. x方向和y方向的一、二阶导数的中心差分算子分别定义如下

将方程(1)改写为

对二阶导数u_xx和u_yy采用如下逼近：

将(7)，(8)式代入(6)式，考虑其在点(x_i，y_j)的值，得到

为了使(9)式空间保持四阶精度，对u_x和u_y的计算采用如下四阶Padé公式^[9]

考虑(9)式在第n+1时间层的离散值，对u_t采用如下二阶BDF^[10-11]进行离散

舍去高阶项，可得

式(13)即为求解方程(1)的四阶紧致格式，截断误差为O(τ²+h_x⁴+h_y⁴)，本文称之为(2，4)格式. 该格式涉及3个时间层，除了初始时刻的值已知外，还需求得第一时间步的值，才可以向下计算. 因此，考虑(9)式在第$n + \frac{1}{2}$时间层的值，时间导数项采用C-N格式离散，空间项采用加权平均方法离散，即可得到

其中G为(9)式的右端项.

在文献[12]中已经证明当K≤6(K代表精度)时，BDF是无条件稳定的. 另外，由式(13)可以看出，在每个时间步上，该格式为5点模板的全隐格式. 为了得到u(x，y，t)的计算值，(14)式中出现的u_x和u_y除需知道其内点值，还需知道其在边界点处的值，为保持与内点差分格式同样的精度，对边界上的u_x，u_y采用一致四阶边界条件^[2]计算.

为了得到方程(1)的六阶精度的格式，需由Taylor级数展开得到一、二阶导数的六阶近似公式

将(15)-(18)式代入(6)式，有

为使(19)式具有六阶精度，需对其中的三阶导数项u_xxx和u_yyy进行四阶离散，对五阶导数项u_x⁽⁵⁾和u_y⁽⁵⁾、六阶导数项u_x⁽⁶⁾和u_y⁽⁶⁾进行二阶离散，为此采用如下离散公式

将(20)-(25)式代入(19)式，考虑其在点(x_i，y_j)的值，即可得到如下半离散的紧致格式

为了使(26)式具有六阶精度，对u_x和u_y采用文献[9]中的六阶差分公式计算，u_xx和u_yy采用文献[13]中的六阶差分公式计算

考虑(26)式在第n+1时间层的值，对u_t采用三阶BDF^[10]进行离散

略去高阶项，可得

(32) 式即为求解方程(1)的六阶紧致格式，截断误差为O(τ³+h_x⁶+h_y⁶)，本文称之为(3，6)格式. 由(32)式可以看出，在每一个时间步上，该格式仍为5点模板的全隐格式. 该格式涉及4个时间层，除了初始时刻的值已知外，还需求得第一、第二时间层的值，方可向下计算. 为此，第一、第二时间层中u_t分别用(14)，(12)式离散，并分别令n=0和n=1，可得上述2个时间步的计算值. 由文献[12]可知，(32)式也是无条件稳定的. 尽管前两个时间步精度不够三阶，但只用其完成前两个时间步的计算，当时间推进到第3个时间步以后，全部采用三阶BDF计算，因此并不影响格式的整体精度，这一点在文献[10-11]中已经得到了验证，本文也会在后面的算例中进行验证. 为了得到u(x，y，t)的计算值，(32)式中出现的u_x和u_y以及u_xx和u_yy除需知道其内点值，还需知道其在边界点处的值，为保持与内点差分格式同样的精度，边界上的u_x，u_y，u_xx和u_yy采用六阶精度的边界格式^[9]计算.

本文将利用以下4个问题进行数值实验，验证(2，4)格式和(3，6)格式的稳定性和有效性，文中涉及到的误差及收敛阶定义如下：

1) 最大绝对误差：

2) L₂范数误差：

3) 收敛阶：

其中U_i，j^M表示点(x_i，y_j，t_M)处的精确解，u_i，j^M表示点(x_i，y_j，t_M)处的数值解，E₁和E₂分别表示空间步长为h₁和h₂时相对应的最大绝对误差或L₂误差，计算时x方向和y方向取相同空间步长h. 所有数值算例的程序均使用Fortran77计算机语言编写，在具有8GB内存、Intel Core i5-8250u处理器的电脑上调试运行.

问题1   考虑如下非齐次对流扩散问题

其精确解为u(x，t)=e^-txy(1-x)(1-y)，初边值条件及右端项f(x，y，t)均由精确解给出.

表 1给出了问题1当τ=h²，t=0.5时的计算结果. 从表中可以看出，本文(2，4)格式和文献[6]格式在空间上均达到了四阶精度，但本文(2，4)格式的计算结果比BTCS格式和文献[6]格式更好；本文(3，6)格式在空间上达到了六阶精度(网格为64时的数值已经达到机器精度，所以收敛阶受到影响不准确)，且最大绝对误差比(2，4)格式的小2~3个数量级，计算结果更精确. 当h=0.01，t=0.5时，不同时间步长τ下的L_∞误差、收敛阶及CPU时间由表 2给出. 从表中可以看出，本文(2，4)格式时间上达到的精度为二阶，本文(3，6)格式时间上达到的精度为三阶，这与理论分析一致；另外当τ较大时计算收敛慢，所用的CPU时间相对较长，计算过程中(3，6)格式需要计算在节点处的一、二阶导数值，因此所用的计算时间比(2，4)格式长.

问题2   考虑如下变系数对流扩散问题

其精确解为u(x，t)=txy(1-x)(1-y)e^x+y，初边值条件及右端项f(x，y，t)均由精确解给出.

表 3给出了问题2当τ=h²，t=0.25时本文格式与C-N格式和BTCS格式的L_∞误差及收敛阶的比较. 从表中可以看出，C-N格式和BTCS格式在空间上达到的精度均为二阶，本文(2，4)格式在空间上达到的精度为四阶，而本文(3，6)格式空间上达到的精度为六阶，且(3，6)格式的计算结果误差更小，充分验证了本文两种格式的精确性和有效性. 另外，上述两个例子的计算结果进一步说明低精度的启动步并不影响格式的整体精度.

问题3   考虑如下高斯脉冲问题

其精确解为$u\left( {x, {\rm{ }}y, {\rm{ }}t} \right) = \frac{1}{{4t + 1}}{{\rm{e}}^{\frac{{ - {{(x - pt - 0.5)}^2} + {{\left( {y - qt - 0.5} \right)}^2}}}{{\alpha \left( {4t + 1} \right)}}}}$，初边值条件由精确解给出.

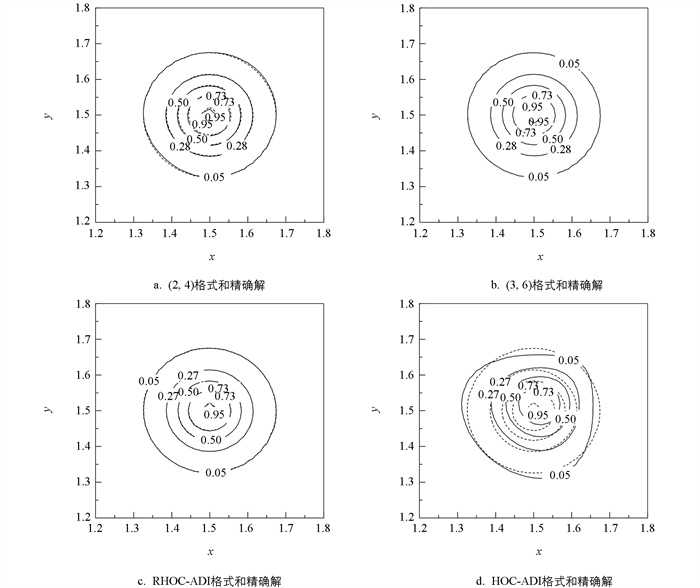
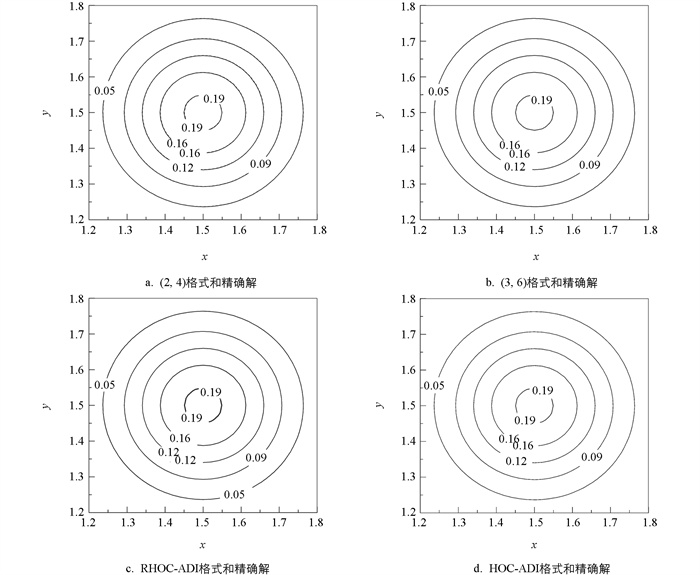
表 4给出了问题3当h=0.02时对不同的t，p，q，τ，高阶紧致差分格式(HOC-ADI)^[4]、有理型高精度紧致差分格式(RHOC-ADI)^[5]及本文(2，4)格式和(3，6)格式的L_∞误差和L₂误差的比较. 从表中可以看出，对于给定的t，p，q，τ，本文(2，4)格式的计算误差比文献[4]格式小，但比文献[5]格式的计算误差略大，(3，6)格式的计算结果明显比文献[4]和文献[5]格式的计算结果更精确. 定义配克立数(Peclet number)为$Pe = \frac{{ph}}{\alpha } = \frac{{qh}}{\alpha }$，图 1和图 2给出了问题3当配克立数Pe分别为2和2 000时，在计算区域1.2≤x，y≤1.8内，不同格式计算解和解析解的等值线，其中虚线所示为解析解，实线所示为计算解. 从图 1可以看出，当Pe=2时，本文(2，4)格式、(3，6)格式、文献[4]格式以及文献[5]格式的计算解均能与解析解吻合得很好，能准确捕获移动脉冲，产生以(1.5，1.5)为中心的脉冲；随着Pe增大到2 000，从图 2可以看出(2，4)格式的计算解与解析解之间的吻合度产生了微弱的偏差，文献[4]格式的计算解与解析解之间产生了相当大的偏差，而本文(3，6)格式和文献[5]格式的计算解仍能与解析解高度吻合，说明本文(3，6)格式与文献[5]格式一样能有效地模拟此类波的传播问题.

问题4  考虑如下非线性方程

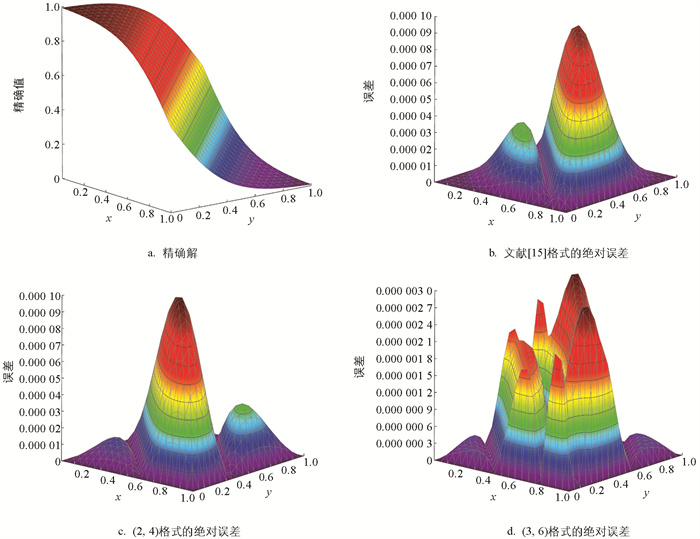
其精确解为$u\left( {x, {\rm{ }}y, t} \right) = \frac{1}{{1 + {{\rm{e}}^{\frac{{x + y - t}}{{2\alpha }}}}}}$，初边值条件由其给出.

表 5给出了问题4当t=1，τ=h²时，本文(2，4)格式和(3，6)格式在α分别取1和0.1时的最大绝对误差与收敛阶. 从表中可以看出，本文(2，4)格式在空间上达到的精度是四阶，(3，6)格式达到的精度是六阶(网格为64，α=1时最大绝对误差的值已经达到机器精度)，这与理论推导是一致的，从表中还可以看出，α=1时所用的CPU时间比α=0.1时的长，(3，6)格式的CPU时间比(2，4)格式的长. 表 6给出了当N=7，τ=0.01，α=1时，t=15和t=20的计算解与精确解的绝对误差. 表中数据表明，本文(2，4)格式的计算误差比文献[14]格式小5~6个数量级，与文献[15]格式的计算结果大致相当；本文(3，6)格式的计算结果比文献[14]格式小7~9个数量级，比文献[15]格式小2~3个数量级. 因此，对于此类非齐次边界的Burgers方程，本文两种高精度紧致差分格式非常有效. 图 3给出了N=20，t=1，τ=0.01，α=0.1时本文两种格式的绝对误差和文献[15]格式的绝对误差比较，从图中可以看出，本文(2，4)格式的绝对误差与文献[15]格式的绝对误差大致相当，但本文(3，6)格式的计算结果更加精确，绝对误差更小.

本文针对二维非稳态变系数对流扩散方程，对时间的离散分别采用二阶BDF和三阶BDF，对空间的离散分别采用四阶紧致差分公式和六阶紧致差分公式，得到了两种无条件稳定的紧致差分格式，格式的截断误差分别为O(τ²+h_x⁴+h_y⁴)和O(τ³+h_x⁶+h_y⁶). 最后通过4个数值算例验证了本文格式的精确性和稳定性. 计算结果显示，本文四阶格式与文献中四阶格式具有相同精度，而本文六阶格式较文献中格式具有更高精度.