首先利用椭圆型方程的极大值原理和比较原理得到方程(2)非负解的一个先验估计.

定理 1  ^[11]假设(u，v)是方程(2)的一个非负解，则(u，v)满足

(i) 0 < u < θ < $\frac{{r - b}}{a} $.

(ii) 0 < v < v₀∶= $ c + \frac{{md\left( {r - b} \right)}}{{a + p\left( {r - b} \right)}}$. 如果c>λ₁，则v>θ_c.

在利用不动点指标理论之前，引入以下记号.

设E是Banach空间，W⊂E是一个闭凸子集. 如果∀α≥0均有αW⊂W，那么称W为楔，并且如果W∩{-W}=0，那么称楔W为锥. 对于任意的点y∈W，定义楔W_y={x∈E：存在γ>0使得y+γx∈E}和S_y={x∈W_y：-x∈W_y}. 设F：W→W是一个紧线性算子，且有一个不动点y，F关于点y的Fréchet导数为L. 设L：W_yW_y是紧线性算子，称L具有α性质，如果存在t∈(0，1)，w∈W_y\S_y，使得w-tTw∈S_y.

引理 1  ^[12]设q(x)∈C(Ω)，M是正常数，使得-q(x)+M>0在Ω上成立，则下面的结论成立：

1) λ₁(q(x)) < 0⇒r[(-Δ+M)^-1(-q(x)+M)]>1.

2) λ₁(q(x))>0⇒r[(-Δ+M)^-1(-q(x)+M)] < 1.

3) λ₁(q(x))=0⇒r[(-Δ+M)^-1(-q(x)+M)]=1.

引理 2  ^[12]如果I-L在W_y上可逆，那么

1) 若L有α性质，则index_W(F，y)=0.

2) 若L没有α性质，则index_W(F，y)=(-1)^σ，其中σ是L所有大于1的特征值的代数重数之和. 利用拓扑度理论得到共存解的存在性，首先引入以下记号：

① X∶=C₀(Ω)⊕C₀(Ω)；

② W∶=P₁⊕P₂，这里P_i={φ∈C₀(Ω)：φ(x)≥0，x∈Ω}；

③ D∶=(u，v)∈X：u≤ $ \frac{{r - b}}{a}$，v≤v₀∶= $c + \frac{{md\left( {r - b} \right)}}{{a + p\left( {r - b} \right)}} $；

④ D′∶=(intD)∩W.

对于任意t∈[0, 1]，定义一个正紧算子F_t：D′W，则

其中M充分大使得M=max{r-b，v₀}. 利用标准椭圆型方程理论，可知F_t是一个完全连续算子. 设t=1时，F=F₁，因此，(u，v)是方程(2)的正解当且仅当F在D′内有一个不动点. 设F关于(u，v)的Fréchet导数为F′(u，v)，则

引理 3   index_W(F，D′)=1.

证   利用Leray-Schauder度的同伦不变性，得到

当t∈[0, 1]足够小时，得到

设

利用引理1，得到r(L₀) < 1，I-L₀在W_(0，0)上是可逆的，L₀在W_(0，0)上没有α性质，利用引理2，得到index_W(F，D′)=1. 证毕.

引理 4   若r-b>λ₁或c>λ₁，则index_W(F，(0，0))=0.

证易知F(0，0)=(0，0)，并且

假设存在(ξ，η)∈W_(0，0)使得F′(0，0)(ξ，η)=(ξ，η)，等价于(ξ，η)满足

如果ξ>0，那么r-b=λ₁，这与r-b=λ₁矛盾，所以ξ≡0. 类似地，若η>0，c=λ₁，这与c>λ₁矛盾，所以η≡0. 因此，I-L₀在W_(0，0)是可逆的.

设T_r-b=(M-Δ)^-1(r+b+M). 因为r-b=λ₁，所以r₀∶=r(T_r-b)>1，且主特征函数ξ_r-b>0，ξ_r-b∈P₁\{0}.

设t₀=1/r₀∈[0, 1]，则(ξ_r-b，0)∈S(0，0)=(0，0)，即F′(0，0)具有α性质，因此index_W(F，(0，0))=0. 证毕.

引理 5   假设r-b=λ₁，

(i) 若c>λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $，则index_W(F，(θ，0))=0.

(ii) 若c < λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $，则index_W(F，(θ，0))=1.

证   (i) 假设存在(ξ，η)∈W_(θ，0)使得F′(θ，0)(ξ，η)=(ξ，η)，等价于(ξ，η)满足

若η 0，注意到η∈P₂，c=λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $，这与假设条件矛盾，所以η≡0. 此时(3)式的第一个方程可以简化为-Δξ=(r-b-2aθ)ξ，因为特征值λ₁(2aθ+b-r)>λ₁(aθ+b-r)=0，所以ξ≡0. 因此(ξ，η)≡(0，0)和I-F′(θ，0)在W_(θ，0)是可逆的.

通过引理1和c>λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $，得到

利用Krein-Rutman理论知存在ψ>0，ψ∈P₂\{0}使得

设t₁= $ \frac{1}{{{r_1}}}$∈[0, 1]，则(0，ψ)∈W_(θ，0)\S_(θ，0)和(I-t₁F(θ，0))(0，ψ)∈S_(θ，0)，即F′(θ，0)有α性质，因此index_W(F，(θ，0))=0.

(ii) 与(i)类似，很容易证明当c < λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $时F′(θ，0)没有特征值超1，所以σ=0，其中σ是F′(θ，0)所有实特征值的代数重数之和，因此引理得证. 证毕.

引理 6   假设c>λ₁，

(i) 若λ₁ $ \left( {b - \frac{r}{{1 + k{\theta _c}}} + \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$ < 0，则index_W(F，(0，θ_c))=0.

(ii) 若λ₁$ \left( {b - \frac{r}{{1 + k{\theta _c}}} + \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$>0，则index_W(F，(0，θ_c))=1.

证 (i)当(u，v)=(0，θ_c)时，通过简单的计算得到

首先证明I-F′(0，θ_c)在W_(0，θc)是可逆的.

假设存在(ξ，η)∈W_(0，θc)使得F′(0，θ_c)(ξ，η)=(ξ，η)，等价于(ξ，η)满足

如果ξ 0，那么b=λ₁ $ \left( {\frac{r}{{1 + k{\theta _c}}} - \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$，这与假设条件矛盾，所以ξ≡0. 类似地，若η 0，则0是下面特征值问题的一个特征值

这与λ₁(2θ_c-c)>λ₁(θ_c-c)=0矛盾，所以(ξ，η)≡(0，0).

其次证明F′(0，θ_c)有α性质.

利用λ₁ $ \left( {b - \frac{r}{{1 + k{\theta _c}}} + \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$ < 0和引理1，得到

利用Krein-Rutman理论，则存在φ>0， φ∈P₂\{0}使得

设t₂= $\frac{1}{{{r_2}}} $∈[0, 1]，则(φ，0)∈W_(0，θc)\S_(0，θc)和(I-t₂F(0，θ_c)(φ，0))∈S_(0，θc). 因此F′(0，θ_c)具有α性质，由引理2可得index_W(F，(0，θ_c))=0.

(ii) 与(i)类似，很容易得到当λ₁ $ \left( {b - \frac{r}{{1 + k{\theta _c}}} + \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$>0时，F′(0，θ_c)没有特征值超过1，所以σ=0，其中σ是F′(0，θ_c)所有实特征值的代数重数之和. 因此index_W(F，(0，θ_c))=1. 证毕.

定理 2   设r-b=λ₁，对于任意的x∈Ω，有

(i) 如果λ₁$\left( { - \frac{{md\theta }}{{1 + p\theta }}} \right) $ < c < λ₁，那么方程(2)除了(0，0)，(θ，0)外，至少还有一个正解.

(ii) 如果c>λ₁和λ₁ $ \left( {b - \frac{r}{{1 + k{\theta _c}}} + \frac{{m{\theta _c}}}{{1 + q{\theta _c}}}} \right)$ < 0，那么方程(2)除了(0，0)，(θ，0)，(0，θ_c)外，至少还有一个正解.

证   利用拓扑度理论，得到

其中(u_i，v_i)是F在D′内的所有不动点. 如果条件(i)成立，利用引理3-6，那么

因此，方程(2)在D′至少有一个正解.

如果条件(ii)成立，则利用引理3-6，那么

因此，方程(2)在D′至少有一个正解. 证毕.

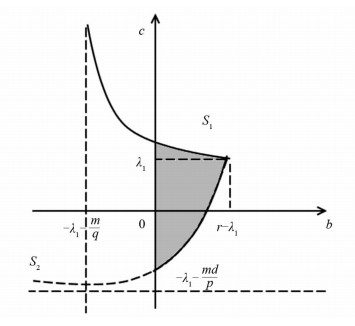
为了研究定理2的意义，在bc-平面内定义：

利用文献[13]中的方法，我们可以得到下面的引理：

引理 7   集合S₁形成一条有界的曲线

其中c=c_*(b)是关于b∈ $\left( { - {\lambda _1} - \frac{m}{q}, r - {\lambda _1}} \right) $的正连续函数且满足下面的性质：

(i) c=c_*(b)关于b∈$\left( { - {\lambda _1} - \frac{m}{q}, r - {\lambda _1}} \right) $是严格单调递减，

(ii) c_*(r-λ₁)=λ₁，c_* $\left( { - {\lambda _1} - \frac{m}{q}} \right) $.

证   设S₁(b，c)=λ₁ $ \left( {b{\rm{ + }}\frac{{m{\theta _c}}}{{1 + q{\theta _c}}} - \frac{r}{{1 + k{\theta _c}}}} \right)$，由θ_λ1=0和c>λ₁可得

因此S₁(b，c)是关于b和c单调递增的. 设b₀是任意固定的实数，若λ₁+b₀-r < 0，即b₀ < r-λ₁，若

即

则利用零点存在定理可得，存在c₀∈(λ₁，∞)使得S₁(b₀，c₀)=0和S₁(b₀，c)≥0，因此，由隐函数定理可知，方程S₁(b，c)=0确定了一个光滑函数c=c_*(b)使得下面结论成立：

其中δ>0. 因为b₀∈ $ \left( { - {\lambda _1} - \frac{m}{q}, r - {\lambda _1}} \right)$的任意性，则当b∈$ \left( { - {\lambda _1} - \frac{m}{q}, r - {\lambda _1}} \right)$时，存在唯一一个光滑函数c=c_*(b)使得S₁(b，c_*(b))=0，对S₁(b，c_*(b))=0关于b微分(或利用隐函数可微性定理)得

即

又因为S_1b(b，c_*(b))>0和S_1c(b，c_*(b))>0，因此c′_*(b) < 0，即c=c_*(b)关于b∈$ \left( { - {\lambda _1} - \frac{m}{q}, r - {\lambda _1}} \right)$是严格单调递减. 很容易得证c_*(r-λ₁)=λ₁和c_* $ \left( { - {\lambda _1} - \frac{m}{q}} \right)$=∞成立. 证毕.

引理 8   集合S₂形成一条有界的曲线

其中b=b^*(c)是关于c∈ $\left( { - {\lambda _1} - \frac{m}{q}, {\lambda _1}} \right) $的正连续函数，且满足下面的性质：

(i) b^*(c)关于c∈ $ \left( { - {\lambda _1} - \frac{m}{q}, {\lambda _1}} \right)$是严格单调递增，

(ii) b^*(λ₁)=r-λ₁，b^* $ \left( { - {\lambda _1} - \frac{m}{q}} \right)$=-∞.

推论 1   设r-b=λ₁，(b，c)位于图 1坐标系内的阴影区域，则原方程(2)至少存在一个共存解.

$ {\lambda _1} - \frac{{md}}{p}$的正负性影响的是曲线S₂的取值范围，若$ {\lambda _1} - \frac{{md}}{p}$>0，则b^*(c)>0；若$ {\lambda _1} - \frac{{md}}{p}$=0，则b^*(c)穿过原点；若$ {\lambda _1} - \frac{{md}}{p}$ < 0，则b^*(c)图像如图 1所示.

定理 3   设r-b=λ₁，r-b> $ {\lambda _1} + \frac{{md{v_0}}}{{1 + q{v_0}}}$.

令

如果$ \frac{{md{v_0}}}{{1 + q{v_0}}}$ < a且m²Λ(1+d)+2rkmΛ(1+p) < 4a，那么方程(2)存在唯一正解.

证   因为

则由定理1可知，正解的存在性显然.

设(u₁，v₁)和(u₂，v₂)是方程(2)的正解. 由椭圆型方程的比较原理可得

令A=u₁-u₂，B=v₁-v₂，则A，B满足T₁A+T₃=0和T₂B+T₄=0，其中

因为(u₁，v₁)是方程(2)的正解，所以存在(ξ，η)满足

利用特征值的变分原理可得：

和

在T₁A+T₃=0两边同乘A，并联立(4)式可得：

其中

令

故W₁>0. 同理，在T₂B+T₄=0两边同乘B，并联立(5)式可得：

其中

设I=∫_Ω[W₁u₂A²+(W₂u₂+W₄v₂)AB+W₃v₂B²]dx，由(6)式和(7)式知I≤0，则

因为Δ≤0，所以I≡0，因此A=B=0，即(u₁，v₁)=(u₂，v₂). 证毕.

本文研究了Dirichlet边界条件下，一类带有恐惧效应模型共存解的存在性和唯一性. 由定理2和推论1的研究结果可知：(i)当反应扩散模型不受恐惧效应影响时，即当k=0时，食饵和捕食者满足一般种群数量的增长规律；(ii)当食饵和捕食者的内禀增长率在一定范围内变化，且恐惧效应对食饵的影响不大时，食饵和捕食者在区域内可以共存；(iii)当恐惧效应强度过高时，捕食者和食饵的种群数量变化更加丰富，需要更进一步的研究.