-
张量是数值多重线性代数的主要研究对象,其在量子力学、心理测量学、化学计量学、信号处理、高阶统计等领域有重要应用[1-3]. 张量是向量和矩阵的高阶推广,它的许多性质与矩阵情形类似,但也有很大不同[4]. 张量相关问题的研究要比矩阵情形复杂得多. 目前,在张量分解、张量的低秩逼近、张量互补问题、张量特征值问题和张量方程等方面已有诸多研究成果[4-9]. 本文考虑基于Einstein积[10]的一类张量方程的求解问题.
为了表述方便,首先介绍本文用到的一些记号和定义. m-阶I1×I2×…×Im-维复张量A=(ai1i2… im),ai1i2… im∈
$ \mathbb{C} $ ,1≤ij≤Ij(j=1,2,…,m). 我们用$ \mathbb{C} $ I1×I2×…×Im表示所有m-阶I1×I2×…×Im-维复张量的全体. 本文中In=(ei1i2… inj1j2… jn)∈$ \mathbb{R} $ I1×I2×…×In×I1×I2×…×In表示单位张量,它的元素定义为ei1i2… inj1j2… jn=$ \mathop \Pi \limits_{k = 1}^n $ δikjk,这里δikjk=1如果ik=jk,否则δikjk=0.若张量A=(ai1i2… imj1j2… jn)∈
$ \mathbb{C} $ I1×I2×…×Im×J1×J2×…×Jn,B=(bj1j2… jnk1k2… kp)∈$ \mathbb{C} $ J1×J2×…×Jn×K1×K2×…×Kp,则它们的Einstein积A*nB为I1×I2×…×Im×K1×K2×…×Kp-维张量,依据文献[7]定义其元素为进一步,设张量S=(ai1i2… imj1j2… jn),T=(bk1k2… kml1l2… ln)且S,T∈
$ \mathbb{C} $ I1×I2×…×Im×J1×J2×…×Jn,则其内积定义为张量的内积诱导出张量的Frobenius范数,即对于张量T有‖T‖=
$\sqrt {\left\langle {\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{T}}} \right\rangle } $ .定义1 设张量A=(ai1i2… imj1j2… jn)∈
$ \mathbb{C} $ I1×I2×…×Im×J1×J2×…×Jn,则其共轭转置AH定义为若张量A∈
$ \mathbb{C} $ I1×I2×…×Im×I1×I2×…×Im满足条件AH=A,则称之为Hermitian张量.若定义1中A是实张量,则共轭转置退化为转置[7]. 值得一提的是,最新的研究发现,Hermitian张量在量子纠缠中有实际应用[11]. 本文考虑张量方程
的Hermitian解,这里A,B∈
$ \mathbb{C} $ P1×P2×…×Pm×I1×I2×…×In为已知张量,X∈$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In为未知的Hermitian张量. 张量方程(1)在控制系统、连续力学等领域有实际应用[7, 11]. 例如,对于2-维泊松方程Ω={(x,y)|0≤x,y≤1},利用中心差分格式,可以离散为张量方程[7]
这里张量A∈
$ \mathbb{R} $ N×N×N×N的非零元为F∈
$ \mathbb{R} $ N×N,对于没有约束条件的张量方程(1),文献[7]引入了张量逆的概念,得到了它的最小二乘解. 进一步,作为张量逆的推广形式,文献[12]提出了张量的Moore-Penrose广义逆,并讨论了张量方程(1)的可解性及其通解形式.在图像处理等领域的应用中,考虑方程解的特殊结构是降低算法复杂度的重要途径[13],但是对于带有约束条件的形如方程(1)的张量方程求解问题尚无研究. 借助张量的Moore-Penrose广义逆的性质,我们将建立张量方程组(1)有Hermitian解的充要条件,并得到有解时的一般解表达式. 进一步,将考虑张量方程(1)约束下的张量逼近问题.
设X0∈
$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In为一给定张量,求Hermitian张量$ {\mathop {\boldsymbol{X}}\limits^ \wedge } $ ∈$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In使之满足等式其中Θ表示张量方程(1)的所有Hermitian解的集合.
矩阵最佳逼近问题在有限元、控制论等领域具有实际应用,且已被深入研究[14-16]. 张量最佳逼近问题(3)可以看作是矩阵情形的直接推广形式,同时也可以看作是张量完全问题、张量低秩逼近问题等应用型问题的一般形式[17-19]. 在式(3)中,张量X0由实际测量或试验观测所得,但由于误差原因,它往往不满足所要求的特殊结构或性质,而
$ {\mathop {\boldsymbol{X}}\limits^ \wedge } $ 是满足实际需求的张量. 若解集合Θ非空,可以证明上述张量逼近问题的解是唯一的,且可以利用已知张量的Moore-Penrose逆具体表示.
全文HTML
-
为了研究Hermitian张量约束下的张量方程(1)的求解问题,我们首先引入如下引理,这对得出本文的主要结果是十分重要的.
引理1[19] 设F∈
$ \mathbb{C} $ I1×I2×…×Im×J1×J2×…×Jn,G∈$ \mathbb{C} $ K1×K2×…×Kp×L1×L2×…×Lq,E∈$ \mathbb{C} $ I1×I2×…×Im×L1×L2×…×Lq,则张量方程F*nZ*pG=E有解当且仅当F*nF+*mE*qG+*pG=E,此时它的通解为其中张量Y∈
$ \mathbb{C} $ J1×J2×…×Jn×K1×K2×…×Kp是任意的.引理2 设张量A,B∈
$ \mathbb{C} $ P1×P2×…×Pm×I1×I2×…×In,则张量方程(1)有Hermitian解的充要条件为张量方程组有一般解.
证 若张量方程(1)有Hermitian解,则显然张量方程组(4)有解. 反之,若M为张量方程组(4)的一个解,即A*nM=B,M*nAH=BH. 令
$ \mathit{\boldsymbol{Y}} = \frac{{\mathit{\boldsymbol{M}} + {\mathit{\boldsymbol{M}}^{\rm{H}}}}}{2} $ ,显然Y是一个Hermitian张量且满足式(1),即张量Y为它的一个Hermitian解.由引理2可见,求解张量方程(1)的Hermitian解等价于求解张量方程组(4)的一般解. 基于此,我们得到如下定理.
定理1 设张量A,B∈
$ \mathbb{C} $ P1×P2×…×Pm×I1×I2×…×In,则张量方程(1)有Hermitian解的充要条件为此时它的一般解为
其中:
$\mathit{\boldsymbol{\bar {\bar X}}}$ =$ \frac{1}{2} $ [A+*mB+BH*m(AH)++A+*mB*n(I1-A+*mA)+(I1-A+*mA)*nBH*m(AH)+],I1∈$ \mathbb{R} $ I1×I2×…×In×I1×I2×…×In为单位张量,V∈$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In是任意的Hermitian张量.证 根据张量Moore-Penrose广义逆的性质和引理1可知,张量方程(1)有解的充要条件为
此时
这里Z∈
$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In为任意张量. 当式(7)成立时,结合式(4)可知A*nBH=B*nAH,即知式(5)成立.进一步,将式(8)代入式(4)的第二个方程X*nAH=BH并整理得
这是关于变量Z的张量方程. 在条件(7)成立时,该方程总是有解的,且由引理1知其一般解为
其中W∈
$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In为任意张量. 将式(9)代入式(8)可得结合引理2的证明过程可得式(6)成立. 命题得证.
注 根据Moore-Penrose广义逆的性质有〈
$\mathit{\boldsymbol{\bar {\bar X}}}$ ,(I1-A+*mA)*nV*n(I1-A+*mA)〉=0,故$\mathit{\boldsymbol{\bar {\bar X}}}$ 为张量方程(1)的Hermitian极小范数解.接下来考虑张量的最佳逼近问题(3). 首先引入如下引理.
引理3[19] 设E∈
$ \mathbb{C} $ I1×I2×…×Im×J1×J2×…×Jn,F∈$ \mathbb{C} $ I1×I2×…×Im×I1×I2×…×Im,G∈$ \mathbb{C} $ J1×J2×…×Jn×J1×J2×…×Jn且满足则‖E-F*mE*nG‖=
$ \mathop {\min }\limits_{\boldsymbol{H} \in \mathbb{C} ^{ {I_1} \times {I_2} \times \cdots \times {I_m} \times J_1 \times J_2 \times \cdots \times {J_n}} } \, $ ‖E-F*mH*nG‖当且仅当F*m(E-H)*nG=O.根据引理3,我们可以证明张量逼近问题(3)的解是唯一的,并给出解的具体形式.
定理2 给定张量X0∈
$ \mathbb{C} $ I1×I2×…×In×I1×I2×…×In. 若定理1中的条件(5)成立,则张量最佳逼近问题(3)有唯一Hermitian解$ {\mathop {\boldsymbol{X}}\limits^ \wedge } $ ,即成立,此时
其中张量
$\mathit{\boldsymbol{\bar {\bar X}}}$ 的具体形式见定理1.证 当定理1中的条件(5)成立时,张量方程(1)的解集合Θ是非空的,且容易验证它是一个闭凸集,这说明最佳逼近问题(3)有唯一解. 由式(6)和式(3)可得
因为I1-A+*mA为正交投影张量,故满足引理3中的假设条件,从而有
当且仅当
由式(12)和式(13)可得式(10),而式(6)和式(14)说明最佳逼近问题(10)的唯一解为
利用
$\mathit{\boldsymbol{\bar {\bar X}}}$ 的具体表达式和张量Moore-Penrose广义逆的性质,化简式(15)即知式(11)成立.
-
本节通过数值例子验证所得结论的可行性. 接下来的所有实验数据均是通过配置了Inter(
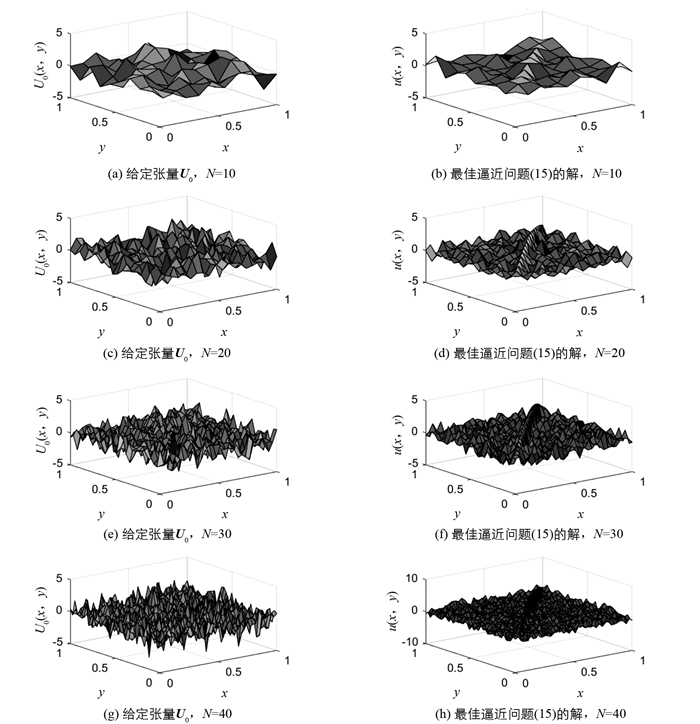
$ \mathbb{R} $ ) Core(TM) i5-4200M CPU与4.00 G内存的电脑上的MATLAB软件编程实现,其中张量积的运算用到了张量工具包[20].例 考虑离散的2-维泊松方程的Hermitian解,即张量方程(2),这里取张量F=eyes(N,N)为单位张量. 另外,给定张量U0∈
$ \mathbb{R} $ N×N随机产生,即U0=randn(N,N),容易验证,已知张量A和F满足定理1中的条件(5),故相应的张量逼近问题有唯一解
$ {\mathop {\boldsymbol{U}}\limits^ \wedge } $ . 对于不同正整数N和张量U0,根据定理2,可以得到上述最佳逼近问题的解(图 1). 图 1展示了最佳逼近解的对称性.
-
本文考虑了基于Einstein积的张量方程A*nX=B关于Hermitian张量X的可解性问题. 利用张量Moore-Penrose广义逆的性质,得到了上述问题有解的充要条件,并得到了它的一般解表达式. 另外,对于任意给定张量,在假定上述条件成立时,讨论了相应的张量最佳逼近问题,证明了解的唯一性,并得到了它的具体表达式. 最后给出实际应用实例验证了本文所得结果的可行性,这些结果对张量相关理论的完善具有重要意义.



 下载:
下载: