高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

成渝地区时空压缩格局的模拟：一个改良的时空图制图模型

,  , 

上一篇

下一篇

葛恒衡, 阎建忠, 王涛. 成渝地区时空压缩格局的模拟：一个改良的时空图制图模型[J]. 西南师范大学学报(自然科学版), 2022, 47(1): 82-90. doi: 10.13718/j.cnki.xsxb.2022.01.011
引用本文: 葛恒衡, 阎建忠, 王涛. 成渝地区时空压缩格局的模拟：一个改良的时空图制图模型[J]. 西南师范大学学报(自然科学版), 2022, 47(1): 82-90. doi: 10.13718/j.cnki.xsxb.2022.01.011
shu
GE Hengheng, YAN Jianzhong, WANG Tao. Simulation of Time-Space Compression Pattern in Chengdu-Chongqing Region: an Improved Time-Space Mapping Model[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(1): 82-90. doi: 10.13718/j.cnki.xsxb.2022.01.011
Citation: GE Hengheng, YAN Jianzhong, WANG Tao. Simulation of Time-Space Compression Pattern in Chengdu-Chongqing Region: an Improved Time-Space Mapping Model[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(1): 82-90. doi: 10.13718/j.cnki.xsxb.2022.01.011
shu

成渝地区时空压缩格局的模拟：一个改良的时空图制图模型

  • 西南大学 资源环境学院，重庆 400715

  • 基金项目: 国家自然科学基金项目(41761144081)
详细信息
    作者简介:

    葛恒衡，主要从事区域地理学研究 .

    通讯作者: 阎建忠，研究员，博士研究生导师; 

  • 中图分类号: X321, U125

Simulation of Time-Space Compression Pattern in Chengdu-Chongqing Region: an Improved Time-Space Mapping Model

  • College of Resources and Environment, Southwest University, Chongqing 400715, China

  • 摘要: 针对已有时空图制图模型中存在的数据来源单一、应用范围受限、数据要求过高等问题，该文提出以路径优化为思路、Dijkstra算法为基础的制图模型改良方法. 改良后的模型通过网络爬取来获得OD(Optical Density)数据；Dijkstra算法被用于实现OD矩阵数据的合并；应用多维尺度度量方法，生成最佳拟合空间；使用七参数空间坐标转换算法将拟合空间点位投影至原始地理空间中，并对拟合误差进行可靠性检验. 最终依据节点的点位位移和拟合空间的扭曲现象，分析多轮区域时空压缩效应的格局. 该文以成渝城市群为例，绘制不同交通网络建设水平下的通行时间时空图，预测规划高铁网建成条件下的未来可达性格局. 该文证实了Dijkstra算法在时空图制图模型上的应用可行性，总结了模型改良后具有降低数据量需求及实现数据合并的优势，探索了多种通行方式下地区时空图及规划条件下预测时空图的模拟方法，扩展了时空图制图法的应用范围.
    Abstract: In view of the shortcomings of single data source, limited application scope and high data requirement in the existing time-space mapping models, an improved mapping model based on path optimization and Dijkstra algorithm has been proposed in this paper. The improved model obtains OD(Optical Density) data through network crawling. Dijkstra algorithm is used to merge OD matrix data. The best fitting space is generated by multi-dimensional scale measurement method. The seven-parameter spatial coordinate transformation algorithm is used to project the points of the fitting space into the original geographic space, and the reliability of the fitting error is tested. Finally, according to the point displacement of nodes and the distortion of the fitting space, the time-space compression effect pattern of the multi-wheel region is analyzed. Taking Chengdu-Chongqing Urban Agglomeration as a case area, the regional time-space map of transit time under different levels of transportation network construction has been drawn in this paper, and the region's future accessibility pattern predicted under the condition of planned high-speed rail network construction. The feasibility of Dijkstra algorithm's application to time-space mapping method has been confirmed, the advantages of the improved model summarized in reducing the demand of data volume and realizing data consolidation, the methods of drawing time-space maps explored under various traffic modes or prediction conditions, and the application scope of time-space mapping method expanded.
  • 加载中

  • 图 1  成渝城市群范围

    下载: 全尺寸图片 幻灯片

    图 2  时空图制图法分析流程

    下载: 全尺寸图片 幻灯片

    图 3  矩阵算法优化思路示意图

    下载: 全尺寸图片 幻灯片

    图 4  拟合空间生成示意图

    下载: 全尺寸图片 幻灯片

    图 5  拟合空间与地理空间对比示意图

    下载: 全尺寸图片 幻灯片

    图 6  时空图上的水平位移和垂直位移

    下载: 全尺寸图片 幻灯片

    表 1  拟合效果分级标准

    Stress值/% 拟合效果
    20 弱
    10 一般
    5 好
    2.5 极好
    0 完美
    下载: 导出CSV

    表 2  公路-铁路出行方式下的时空图分析拟合结果

    分析参数 城市样本数 200
    有效OD数据 19 900
    通行时间数据 公路-铁路通行时间(现状) 公路-铁路通行时间(规划)
    有效性检验 标准拟合误差σ值 0.007 63 0.009 69
    拟合误差系数Stress 0.087 34 0.098 46
    误差分析 绝对拟合误差平均值 +0.38 h +0.26 h
    拟合误差标准差 0.49 h 0.36 h
    95%误差范围b -0.84 h~+1.11 h -0.72 h~+0.73 h
    误差率τ平均值 +0.00% +0.00%
    95% τ值范围b -40.1%~+17.0% -41.5%~+19.5%
    下载: 导出CSV
  • [1] JANELLE D G. Central Place Development in a Time-Space Framework [J]. The Professional Geographer, 1968, 20(1): 5-10. doi: 10.1111/j.0033-0124.1968.00005.x
    [2] 蒋海兵, 张文忠, 祁毅, 等. 区域交通基础设施可达性研究进展[J]. 地理科学进展, 2013, 32(5): 807-817. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DLKJ201305014.htm
    [3] HANSEN W G. How Accessibility Shapes Land Use [J]. Journal of the American Institute of Planners, 1959, 25(2): 73-76. doi: 10.1080/01944365908978307
    [4] 陈卓, 梁宜, 金凤君. 基于陆路综合交通系统的中国城市网络通达性模拟及其对区域发展格局的影响[J]. 地理科学进展, 2021, 40(2): 183-193. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DLKJ202102001.htm
    [5] 吴红波, 郭敏, 杨肖肖. 基于GIS网络分析的城市公交车路网可达性[J]. 北京交通大学学报, 2021, 45(1): 70-77. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT202101009.htm
    [6] 曹芳东, 黄震方, 黄睿, 等. 江苏省高速公路流与景区旅游流的空间关联及其耦合路径[J]. 经济地理, 2021, 41(1): 232-240. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JJDL202101026.htm
    [7] 俞路. 高铁新时代下中国铁路交通可达性分布格局及其均衡程度的研究[J]. 世界地理研究, 2020, 29(6): 1148-1160. doi: 10.3969/j.issn.1004-9479.2020.06.2019312
    [8] 陈伟. 基于可达性的中国城市群空间范围识别研究[J]. 地理研究, 2020, 39(12): 2808-2820. doi: 10.11821/dlyj020200365
    [9] 陈洁, 陆锋. 京津冀都市圈城市区位与交通可达性评价[J]. 地理与地理信息科学, 2008, 24(2): 53-56. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DLGT200802015.htm
    [10] 陆锋, 陈洁. 武汉城市圈城市区位与可达性分析[J]. 地理科学进展, 2008, 27(4): 68-74. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DLKJ200804010.htm
    [11] 蒋海兵, 徐建刚, 祁毅. 京沪高铁对区域中心城市陆路可达性影响[J]. 地理学报, 2010, 65(10): 1287-1298. doi: 10.11821/xb201010013
    [12] TOBLER W. Map Transformation of Geographic Space[D]. Seattle: University of Washington, 1961.
    [13] 朱昱, 游建胜, 李晓. 时间距离地图超制图学研究——以福州、上海间铁路客运为例[J]. 杭州师范大学学报(自然科学版), 2010, 9(3): 231-236. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HSFZ201003013.htm
    [14] 沈陈华, 王旭姣, 司亚莉, 等. 基于旅行者运动轨迹的时间地图变换[J]. 地理研究, 2015, 34(6): 1160-1172. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ201506015.htm
    [15] 周恺, 钱芳芳, 邹宇. 湖南省城镇空间时空压缩特征及其可视化表达——基于时空图分析模型[J]. 地理科学进展, 2014, 33(12): 1666-1675. doi: 10.11820/dlkxjz.2014.12.010
    [16] 周恺, 刘冲. 可视化交通可达性时空压缩格局的新方法——以京津冀城市群为例[J]. 经济地理, 2016, 36(7): 62-69. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JJDL201607008.htm
    [17] 王杰, 杨坤, 孙峰, 等. 一种基于GIS的公交线路规划方法[J]. 广西大学学报(自然科学版), 2019, 44(5): 1269-1275. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GXKZ201905007.htm
    [18] 李骏明, 刘吉夫, 郭兰兰, 等. 基于道路通达性的高原地区震后应急救援方案研究[J]. 自然灾害学报, 2020, 29(4): 113-123. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202004012.htm
    [19] 陈慧灵, 石恩名, 刘望保. 基于"时空图"的广州市社会空间分异[J]. 经济地理, 2020, 40(8): 9-17. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JJDL202008002.htm
    [20] 张文彤, 董伟. 高等学校教材: SPSS统计分析高级教程[M]. 2版. 北京: 高等教育出版社, 2013.
    [21] KRUSKAL J B. Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis [J]. Psychometrika, 1964, 29(1): 1-27. doi: 10.1007/BF02289565
    [22] 高玉祥, 董晓峰, 梁颖. 基于GIS的宁夏路网空间特征研究[J]. 干旱区地理, 2021, 44(1): 268-276. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GHDL202101030.htm
    [23] 谭玮宝, 黄晓燕, 路改改, 等. 秦巴山区交通可达性对人口分布时空格局的影响[J]. 陕西师范大学学报(自然科学版), 2021, 49(2): 15-27. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SXSZ202102004.htm
    [24] 高玉祥, 董晓峰. 高速铁路建设对甘肃省时空可达性的影响作用研究[J]. 北京交通大学学报, 2020, 44(6): 82-89. doi: 10.11860/j.issn.1673-0291.20200004
    [25] 戴智, 江捷, 麦文隽, 等. 基于互联网地图的可达性量化评价方法[J]. 城市轨道交通研究, 2020, 23(12): 28-32. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT202012008.htm
    [26] 可钰, 聂磊, 袁午阳. 基于空铁联运OD可达性的高铁时刻表优化模型[J]. 交通运输系统工程与信息, 2021, 21(1): 23-29. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT202101005.htm
  • 加载中
图( 6) 表( 2)
计量
  • 文章访问数:  428
  • HTML全文浏览数:  428
  • PDF下载数:  56
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-04-11
  • 刊出日期:  2022-01-20

成渝地区时空压缩格局的模拟：一个改良的时空图制图模型

    通讯作者: 阎建忠，研究员，博士研究生导师; 
    作者简介: 葛恒衡，主要从事区域地理学研究
  • 西南大学 资源环境学院，重庆 400715
  • 收稿日期:  2021-04-11
基金项目:  国家自然科学基金项目(41761144081)

摘要: 针对已有时空图制图模型中存在的数据来源单一、应用范围受限、数据要求过高等问题，该文提出以路径优化为思路、Dijkstra算法为基础的制图模型改良方法. 改良后的模型通过网络爬取来获得OD(Optical Density)数据；Dijkstra算法被用于实现OD矩阵数据的合并；应用多维尺度度量方法，生成最佳拟合空间；使用七参数空间坐标转换算法将拟合空间点位投影至原始地理空间中，并对拟合误差进行可靠性检验. 最终依据节点的点位位移和拟合空间的扭曲现象，分析多轮区域时空压缩效应的格局. 该文以成渝城市群为例，绘制不同交通网络建设水平下的通行时间时空图，预测规划高铁网建成条件下的未来可达性格局. 该文证实了Dijkstra算法在时空图制图模型上的应用可行性，总结了模型改良后具有降低数据量需求及实现数据合并的优势，探索了多种通行方式下地区时空图及规划条件下预测时空图的模拟方法，扩展了时空图制图法的应用范围.

English Abstract

    全文HTML

  • 时空压缩(Time-space compression)理论最早由地理学者Janelle[1]于1966年提出，该理论将空间距离解读为时间或空间上的隔离度，以解释交通技术进步条件下通行时间的普遍减少和感知空间的压缩. 时空压缩效应的可视化研究致力于直观表达交通可达性格局，识别交通优势和弱势区域，对改善地区交通均衡性具有重要意义[2]. 时空压缩现象通常伴随着交通网的建设而产生，因此时空压缩可视化可以有效模拟交通规划对地区可达性格局的影响，从而作为道路建设方案的评估依据. 目前，时空压缩可视化研究已经具有广泛而重要的应用价值.

    目前，通常采用可达性格局法(Accessibility pattern map)和等时圈法(Isochrones map)两种思路来实现时空压缩效应的可视化[3-4]. 然而，这两种思路都存在不足. 可达性格局法是基于区域可达性评价的方法. 该方法依据选取的可达性指标来评价各节点的全局可达性，利用空间插值生成完整的可达性格局图，并通过分析格局图中等值线的分布特征来判断时空压缩的方向和强弱[5-7]. 但是，格局法无法表达空间位置间的具体邻近关系，存在着“只见森林不见树木”的局限. 等时圈法是依赖于中心节点的可视化方法，其依据选取的中心城市，以特定通行成本阈值划定等时圈，并以“时圈”特征作为衡量时空压缩方向和强度的依据[8-11]. 但是，该方法依赖于中心城市的存在，不适用于更大尺度下的宏观交通网络的分析，在应用范围上受到极大的限制. 因此，学界一直在寻求新的可视化思路，以弥补上述两种方法的不足.

    时空图制图法(Time-space map)来源于Tobler[12]提出的“时间-空间图”构想. 该方法利用通行成本(时间/距离)来取代欧氏距离，生成具有通行时间或距离概念的可达性功能空间，并通过功能空间的扭曲现象来反映原始地理空间中的时空压缩效应. 事实上，时空压缩可视化在本质上是地理科学中的“超制图”问题[13]. 而时空图制图法不仅更接近于时空压缩效应的“压缩”本质，在可视化表达上也兼顾了“森林”和“树木”两种尺度的变换，从而克服了现有可达性分析思路的不足. 然而，由于数据获取困难，时空图制图法长期以来受到极大的应用限制，在时空压缩研究领域并没有得到广泛应用.

    近年来，一些研究借助于网络云端数据解算和超高的计算机性能，探索了时空图制图法在区域层面时空压缩可视化的方法[14-16]. 但是，这些研究的制图模型普遍存在数据来源单一(如仅依赖公路网，忽略铁路网)、通行数据兼容性差、对数据完整性要求过高等缺陷，这些缺陷限制了时空图制图法的普及与应用，制图结果难以准确反映区域的可达性格局. 在现有模型中，通行数据多依靠网络云端解算获取，制图结果仅能表征单一时间的地区可达性格局，时间连续性差，数据更新困难. 此外，现有的制图实践缺乏对区域未来可达性格局的预测方法，难以模拟交通规划对地区可达性格局的影响，限制了时空图制图法在我国立体交通网大建设背景下的应用潜力.

    为解决时空图制图法的应用难题，本文尝试以路径优化为思路、Dijkstra算法为基础进行时空图制图模型的改良. 事实上，Dijkstra算法作为常用的最短路径解算方法[17-18]，在路网解算及路线规划中已被广泛应用. 例如，王杰等[17]利用Dijkstra算法进行地方公交线路规划的优化，模拟了新增公交线路对公交网出行的影响；李骏明等[18]使用Dijkstra算法模拟了高原地区地震破坏对道路通达性的影响. 这些研究都证实了Dijkstra算法在地区可达性解算及变动模拟等方向上的应用潜力. 因此，在现有模型的基础上，本文通过引入Dijkstra算法，尝试构建OD数据(起点-终点通行数据)矩阵间的运算逻辑与方法，使得改良后的制图模型不仅允许不同通行方式下OD数据的进入，还可以实现OD数据的更新，从而拓展了时空图制图法的应用范围. 基于此，本文以成渝城市群为案例区，采用改良后的时空图制图模型，模拟了不同交通网络建设水平下的区域可达性时空图，证实了改良后的制图模型的可行性和应用价值.

1.   研究范围与方法

    1.1.   研究范围

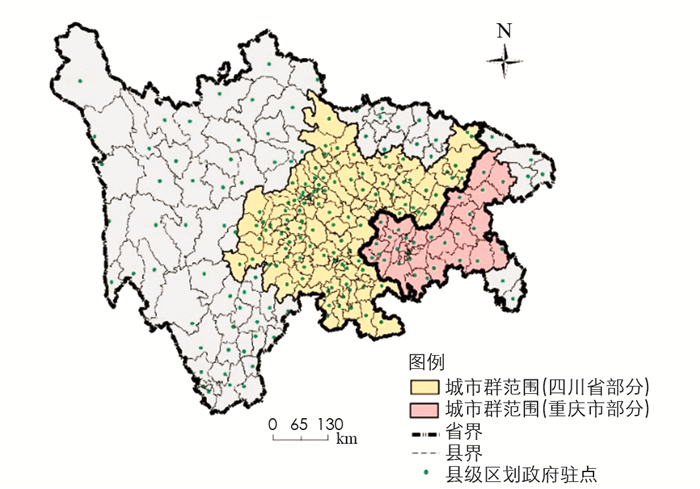
  • 本文以成渝城市群为研究区，将四川省、重庆市范围内共计200个县级行政区划纳入分析. OD矩阵的节点设置为各县级市、区的政府驻点(图 1).

    • 1.2.   研究方法

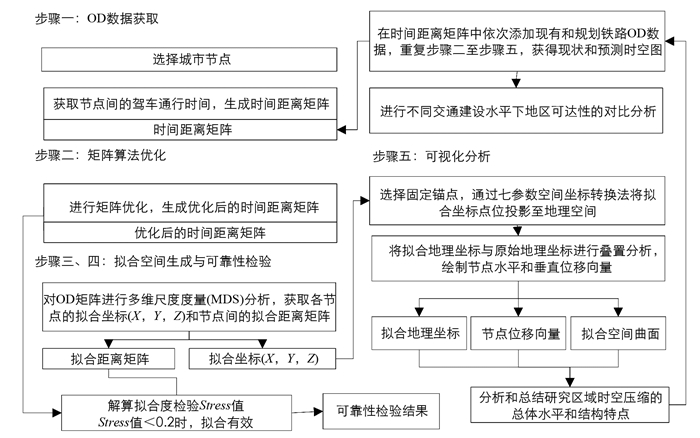
  • 本文建立的时空图制图法分析流程主要包括OD数据获取、矩阵算法优化、拟合空间生成、可靠性检验、可视化分析5个步骤(图 2).

    • 1.2.1.   OD数据获取

  • 在公路网数据的获取上，本文使用百度地图应用程序接口(API)提供的批量算路功能，对节点间的驾车通行时间进行数据抓取，查询并存储最短通行时间，作为通行阻力生成OD矩阵. 现有铁路网数据来源于12306官网在一周内的全部车次信息，查询并存储节点间的铁路车次，并记录车次的预估通行时间. 规划铁路网以川渝地区在“十四五”规划时期内的规划铁路线为准，依据各条线路的设计路程和设计速度对通行时间进行估算，并记录节点间的预估通行时间. 以上数据获取时间皆为2020年8月.

    • 1.2.2.   矩阵算法优化

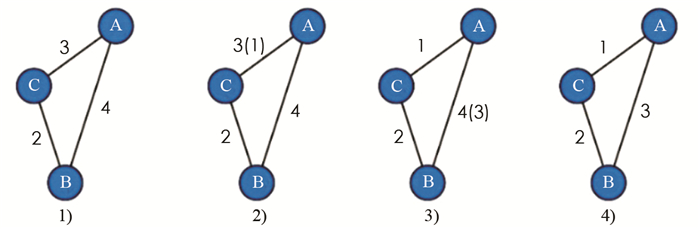
  • 在OD矩阵中，数据的更新和矩阵间数据的合并可被设想为节点间的最短路径问题[17-18]. 基于此设想，本文引入Dijkstra算法对OD矩阵进行迭代优化(图 3)，其基本思路为：

    1) 对固定的交通网而言，解算生成的OD矩阵应是唯一的，且在该矩阵中，任意坐标值的含义都是对应节点间的最短通行时间. 即对于任意两节点A，B而言，无法寻求到任意一节点C，使得通行路径A→C→B的总通行时间比路径A→B更短. 研究者将满足此特征的OD矩阵称为“完美矩阵”.

    2) 交通网的建设将引起OD矩阵的变化. 首先，道路线的建设可被量化为线路上相关节点间直接通行时间的减少. 在OD矩阵中，对应的坐标值应被替换为新的直接通行时间.

    3) 在此基础上，节点间通行状况的改善还会引起除道路线上节点以外附近节点间最短通行时间的减少. 这种扩散效应可以被解释为更优“中转通行方案”存在，即道路线以外的节点可以通过在道路线上寻找“中转通行方案”来减少与其他节点的通行时间. 因此，道路线的改善或新建道路线将使得矩阵不再满足“完美矩阵”条件. 在变动后的矩阵中，存在中转通行路径的通行时间比直接通行路径更短，此时应将直接通行路径对应的矩阵坐标值替换为中转通行路径的通行时间，并可将这种替换称为一次“迭代优化”.

    4) 运算终点的界定. “完美矩阵”条件的再次满足可作为OD矩阵迭代优化的终点. 此时矩阵迭代优化结束，新生成的OD矩阵可代表节点间的可达性水平.

    • 1.3.   拟合空间生成与可靠性检验

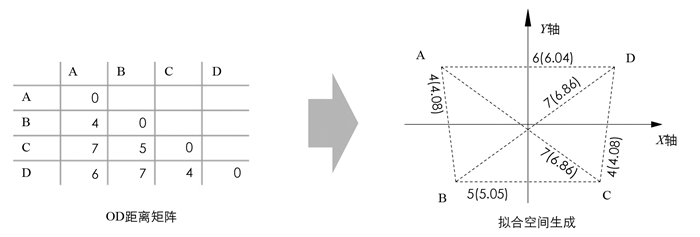
  • 多维尺度度量(MDS)是时空图制图模型常用的拟合空间生成模型[15-16, 19]，本文采用了MDS模型里适合于连续数据的PROXSCAL算法. 该算法依据最小二乘原则，通过多次坐标移动获得一个最佳拟合空间，使各点在拟合空间和原始OD矩阵中通行时间差值的二次方和趋于最小[20]，拟合维度设置为3维(图 4).

    式(1)、式(3)中：n为节点数量；m为通行时间数量；$ {\hat d} $ijk为拟合空间中的通行时间；dij(Xk)为OD矩阵中的通行时间；τ为拟合误差率.

    式(1)中，σ是标准化的原始Stress值，σ值越小，拟合程度越好. 应力系数(Stress)值(式2)是MDS空间构形图拟合度的主要衡量指标，该值越接近于0，拟合效果越好.根据Kruskal[21]提出的MDS分析检验标准，仅Stress < 20%的分析结果才可以接受(表 1). 同时，对拟合误差值及拟合误差率的分布统计可进一步说明拟合坐标的可信度水平.

    • 1.4.   可视化分析

  • ArcGIS软件中提供的ArcScene模块常用于三维空间的可视化分析. 本文利用“自然邻域”空间插值算法，将拟合节点坐标插值生成连续曲面. 在叠置比较上，采用七参数空间坐标转换算法，通过3个节点锚点的设置，完成拟合空间坐标及曲面向地理坐标的投影，连接各节点在不同空间内的位置，分析其时空压缩位移特征. 本文所绘制的成渝城市群时空图均以新津、双流、金牛3个区作为投影锚点来固定时空图中成都市的空间位置，并保证各时空图向地理空间投影的时空转换比例一致，便于时空图间的对比分析.

2.   结果分析

    2.1.   跨出行方式通行时间时空图

  • 基于百度地图API返回的通行时间数据首先可以生成驾车通行时间OD矩阵. 然后，通过矩阵优化算法依次将零散、线性的现有铁路网及规划铁路线OD数据加入OD矩阵，可依次生成在公路-铁路出行方式下的现状和预测通行时间OD矩阵，并绘制现状时空图(图 5a，图 6a)和预测时空图(图 5b，图 6b). 因此，两类时空图的拟合结果都有效，时空图法有效模拟了现状和未来条件下的可达性格局. 拟合结果显示(表 2)，两类时空图的应力系数在可接受范围内，95%的误差均在±1.5 h之内，95%的误差率不超过±45%.

    • 2.2.   现状时空图特征

  • 从现状时空图可知，铁路网和高铁网的加入极大地影响了区域可达性水平和格局，也产生了可达性空间沿铁路线的一轮收敛效应：①拟合空间东西收缩，南部隆起. 现有铁路线多服务于省间交通联系，产生了拟合空间在东西方向上的大幅收缩，使成都、重庆双核间的通行便捷程度显著提高. 川南地区的铁路线通行条件相对较差，使得拟合空间南部出现了显著的隆起现象. 川南点位抬升后与双城圈中心相离，致使该地区与双城圈间通行不便. ②“上半弧”城市集群发育完全. 以川中、川东地区为主体，形成了以成都为中心的弧状城市集群. 该集群北起广元，经绵阳、德阳，过成都，向南囊括眉山地区. 研究者将该点位集群称为“上半弧”. 在“上半弧”范围内，点位集聚程度高，轮廓明显，发育程度完全. ③“下半弧”城市集群开始发育. 重庆地界内出现以重庆江北、渝中区为中心的“下半弧”城市集群密集区. “下半弧”与“上半弧”遥相呼应，但尚未完成对重庆全市及川东南区域内点位的全覆盖，集聚水平也弱于“上半弧”点位集群. ④双城圈特征初显. 在该阶段，双城圈的交通一体化快速发展，成都-重庆双城都市圈初步形成.

    • 2.3.   预测时空图特征

  • 预测时空图表明，规划铁路线的建成将极大地促进成都-重庆双城圈建设和交通一体化的推进进程：①“下半弧”点位密集区发育完全. 重庆“米”字形结构的未来铁路规划将引起以重庆为中心的点位的新一轮集聚，其结果是“下半弧”城市集群内部点位快速集聚，轮廓明显，点位集聚程度与“上半弧”相近. 该集群将完成对重庆全市、川南、川东南区域内点位的覆盖. ②交通“双城圈”格局发育完全. 在规划阶段，以成都市为中心的“上半弧”城市集群和以重庆为主体的“下半弧”城市集群发育成熟，形成独特的交通“双城圈”. 可以预见，在即将形成的“成渝双城圈”内，成都、重庆双核特征突出，核心间联系紧密，相互靠拢，成渝都市圈“双弧双核双集群双城圈”四双交通格局发育完全.

    • 2.4.   区域交通可达性均衡性改善建议

  • 时空图制图法在可视化方向上拥有表达直观及结果可靠的优势，因而可用于区域交通发展水平的均衡性评价，并可成为政府进行道路建设方案选择的可靠依据. 本文基于现状和预测时空图中表达的区域交通建设水平，以促进成渝交通圈持续发展为出发点，对该区域内部陆基道路网络建设提出以下建议：①应加强川西、川南区域与成渝城市群内部间的交通线路建设，以期扩大交通双城圈的辐射范围. ②应继续着力成渝交通圈双核间的对向交通建设，持续降低两个核心间的交通阻力，进一步收缩在时间维度下的交通双城圈范围，促进成渝间信息、物质、人力等各项资源的交流水平. ③在未来的交通线路建设中，还应增强“上下半弧”中各大交通枢纽节点的运输能力，提高城市点位间运输人力及物力的承受能力.

3.   讨论

    3.1.   矩阵优化算法的价值与应用

    3.1.1.   多通行方式下时空图的绘制

  • 在现有的可达性制图实践中，OD矩阵的获取主要存在两种方法. 传统的可达性研究多使用GIS中的网络分析功能实现对地区可达性的解算[4-5, 22-24]. 这种方法要求完整的地区路网矢量数据，且运算时间长，操作复杂. 部分研究尝试突破传统可达性分析的局限性，利用网络云端解算获取OD数据，以降低数据的解算难度，提高数据获取速度[15-16, 25]. 但目前而言，这种方法放弃了对地区路网数据的获取，其生成的OD矩阵中也并不包含地区交通网的矢量信息，因此OD矩阵间相互独立，缺乏矩阵数据的处理方法.

    本文建立的矩阵优化算法通过距离表的建立，可在个人端实现OD矩阵数据间的合并运算，从而使时空图制图模型兼容不同来源的OD矩阵数据，弥补了现有时空图制图法存在的数据来源单一的局限性. 多通行方式下时空图的绘制可增强制图结果与现实情况的吻合度. 在本模型的制图实践中，对驾车、铁路两种通行方式下通行数据进行合并处理，建立的现状时空图更加接近川渝城市群地区可达性的现实状况.

    • 3.1.2.   时空图的更新应用

  • 现有的时空图制图实践[15-16]往往仅对某一交通网水平下的可达性进行分析，并将其拟合点位及拟合空间与原始地理点位或空间进行对比，因此其制图结果更接近于对地区可达性现状水平的可视化，无法进行多轮时空压缩效应的可视化分析. 时空压缩本身作为交通网络建设中所产生的动态效应，具有鲜明的时间特征，对其可视化研究应体现为不同时间截面下地区可达性的对比分析，而这正是现有时空图制图研究中所欠缺的. 本文建立的矩阵优化算法使OD矩阵可以随着交通路网的更新而不断自我更新，且使建立不同时间截面和交通网条件下的时空图成为可能.

    • 3.1.3.   未来时空图的预测

  • 现有的时空图制图模型缺少矩阵数据处理的方法，难以实现对规划条件下未来时空图变化的有效预测，而OD矩阵间的合并运算则可以使规划条件下时空图的预测成为可能. 例如，在本文的制图实践中，通过在成渝城市群地区的OD矩阵中加入规划铁路线通行时间的估算值，成功绘制了在规划铁路网条件下的预测时空图，从而模拟了地区未来的可达性格局.

    矩阵优化算法在预测地区未来可达性上的应用大大扩展了时空图法的应用价值. 对地区未来可达性水平和格局的有效预测，可以模拟不同道路规划方案对地区可达性格局未来的影响，为我国立体交通网络建设中不同道路规划方案的选择提供支撑.

    • 3.1.4.   对通行数据的要求降低

  • 现有的时空图制图方法必须以区域内完整的OD矩阵作为数据基础. 在城市群尺度下，完整的OD矩阵包含的节点众多，道路网数据量大，获取难度极高. 对于数据有所缺漏的OD矩阵，一般无法进行时空图法的制图. 以本文搜集的铁路线通行时间数据为例，所获得的铁路网OD数据只能连通在铁路线上的地区节点，无法生成完整的铁路网OD矩阵. 而矩阵优化算法通过距离表的设置和中转路径的遍历搜索，可以补全OD矩阵在局部的数据缺失，从而降低了时空图制图法对OD矩阵数据的使用要求，扩大了其适用范围. 但是，数据补全可能导致模型的拟合精度降低，也无法保证对于每一节点都能进行补全(必须存在中转路径)，因此其应用还需进行更多的实证研究. 一般而言，OD矩阵的完整性越高，数据量越充足，生成的时空图会具有更高的精度，并更加接近于地区真实的可达性格局. 模型使用者可以根据所需的精度要求，调整进入模型的矩阵数据的完整性，以达到数据搜集工作量的最大节省.

    • 3.2.   时空图制图法模型的不足

  • 本文所提供的时空图制图法模型是一次探索性的研究，存在深入研究的可能性和进一步完善的潜力，但同时也存在着一定的局限性. 首先，在对地区未来可达性格局的预测上，矩阵优化算法对规划条件下的通行时间估计值具有较高的精度要求，不合理、低精度的规划线路信息将极大地破坏拟合点位的可靠性. 同时，矩阵优化算法将理想化的最优通行时间作为标准，忽略了通行成本的消耗(例如铁路票价)和可能的中转成本(例如在通行方式改变下的等待时间)，使得结果过于理想化. 因此，如何在时空图制图模型中进一步考虑除通行时间外其他成本的限制，使模型结果更接近于现实出行策略[26]，将是时空图制图模型继续改良的方向.

4.   结语

  • 在现有制图实践的基础上，本文扩展了时空图制图法改良的新思路，并以成渝城市群为案例论证了该改良方法的可行性和所具有的实践意义.

    1) 在方法创新上，Dijkstra算法的加入拓展了时空图制图模型的应用范围，增强了制图结果的可信度. 新建立的制图模型在道路数据的动态更新、出行方式的兼容性、数据完整性的要求等方面皆优于原有模型，并可准确地对既有道路规划下未来可达性格局进行预测.

    2) 在实证意义上，本文预测了在规划交通网建设水平下成渝交通圈的发展趋势，即在成渝城市群内部将出现拟合点位高度集聚的“上”“下”半弧城市集群，并最终向着一个发育完全的“双弧双核双集群双城圈”四双交通格局持续演进.

参考文献 (26)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回