-
耦合的ODE-PDE系统广泛存在于工程问题中. 近年来,大量文献采用Backstepping变换方法来解决常微分方程和偏微分方程之间的耦合问题. 为满足工程需要,我们利用边界条件设计控制律来控制这些耦合的ODE-PDE系统使其稳定在平衡状态. 边界控制律是由PDE Backstepping控制发展而来[1-4].
ODE-PDE耦合系统边界控制大多是线性的[5-15],然而非线性现象在应用数学和物理中广泛存在. 耦合的线性常微分方程和非线性偏微分方程系统具有丰富的工程应用价值,但由于非线性在数学上是极具挑战性的问题,故关于非线性偏微分方程系统镇定的结果较少[15-22]. 利用边界控制来稳定非线性ODE-PDE耦合系统是一个很有意义的研究领域.
本文对非线性ODE-PDE耦合系统的控制设计类似于文献[7],主要贡献是基于边界反馈控制的方法处理一类包含反应项是不确定的非线性偏微分方程与线性微分方程的耦合系统的局部指数稳定的问题.
因此,本文考虑以下非线性耦合系统的边界控制
其中:向量
$\boldsymbol{X}(t) \in \mathbb{R}^{n}$ 是装置的一个信号;(A,B)是可控制矩阵对($\boldsymbol{A} \in \mathbb{R}^{n \times n}, \boldsymbol{B} \in \mathbb{R}^{n}$ );标量u(x,t)∈$\mathbb{R}$ 是装置的热量;在x=0处,满足Neumann边界条件,α是傅里叶常数,它取决于装置的材料和导热性,CTX(t)是温度装置($\boldsymbol{C}^{\mathrm{T}} \in \mathbb{R}^{n}$ );U(t)是边界控制输入. f(u(x,t))是非线性函数,对于这个系统,非线性f(u)引用文献[15]假定条件.假定1 对于系统(2)中的f(u),存在δ>0和β>1,使得
其中‖·‖将在后面详细说明.
假定1中的第一项表示0是系统(1)-(4)在零输入下的平衡态,第二项意味着f(u)的增长速度并不比u的幂函数快.
系统(1)-(4)代表了一类广泛的耦合非线性ODE-PDE方程,本文主要贡献是基于Backstepping变换的边界控制方法使一类包含不确定反应项的非线性偏微分方程与线性微分方程的耦合系统达到局部指数稳定. 对于ODE-PDE耦合系统Backstepping边界控制律设计方法是可行的[1, 6-7]. 通过引入具有理想稳定性的目标系统,PDE Backstepping变换将系统转化为由核函数和向量值函数耦合的方程. 然后根据目标系统的边界条件得到控制律. 研究PDE Backstepping变换解决耦合ODE-PDE的控制系统是很有价值的.
本文令
全文HTML
-
引入以下Backstepping变换
其中k(x,y)与ϕ(x)是待定的.
将目标系统取为
其中:
选择向量
$\boldsymbol{K}^{\mathrm{T}} \in \mathbb{R}^{n}$ 使得(A+BK)是Herwitz矩阵.现在用变换
$(\boldsymbol{X}(t), u(x, t)) \longrightarrow(\boldsymbol{X}(t), w(x, t))$ ,将(1)-(4)的解转换为(10)-(13)的解,导出函数k(x,y)和ϕ(x),得到控制律.利用(3),(9)式对w(x,t)关于x和t求导
再令
接着控制律被设计为
通过边界条件(13)获得.
-
为了方便,引用文献[14]直接给出(15)式的解. 令
其中I是单位矩阵.
核函数k(x,y)和ϕ(x)分别为
-
同样我们给出逆变换
令
其中I是单位矩阵.
核函数Ψ(x)和n(x,y)分别为
1.1. Backstepping变换
1.2. 核方程的解
1.3. 逆变换
-
为得到稳定性定理,首先给出几个引理.
引理1 函数w(x,t)由(6)式定义,(PB)T和X(t)由(7)式定义,有以下不等式成立
证 现在利用Schwartz’s不等式和Young’s不等式来估计,可得
接着根据w(1,t)=0与Agmon’s不等式,有
然后利用Poincare不等式,可得
因此,不等式(19)成立.
引理2 根据变换(9)与逆变换(18),可得
其中:
证 由变换(9),可以获得
由Holder’s不等式,可以得到
其中:
接着根据Schwartz’s不等式,有
其中:
因此
同理可估计
其中t和‖Ψ‖2由(22)式定义,则(20)式成立.
引理3 H(w(x,t))由(11)式定义,可得
其中:
证
我们令
其中:
利用Holder不等式与Young’s不等式,可得
通过利用(5)式与(20)式来估计‖f(u(x,t))‖22
其中:
由此可得
同理可估计
其中s来自(23)式.
然后
其中ξ是如(25)式所示的常数.
接下来证明目标系统(10)-(13)是局部稳定的.
定理1 存在一个正常数γ且任意的初始条件满足‖ X(0),w(0)‖2≤γ,有下列不等式成立
其中
则目标系统(10)-(13)在‖·‖2意义下是局部指数稳定的.
证
考虑以下Lyapunov函数
其中矩阵P = PT>0满足
且参数a>0是待定的.
矩阵P是(29)式的解,因此
其中λmin(P)与λmax(P)是矩阵P的最小和最大的特征值.
对(28)式关于t求导,则
代入(19),(20)和(24)式可以得到
令a=8‖PB‖2+3,可得
其中ξ由(25)式定义.
根据文献[17]定理,如果V(0)≤σγ2,其中
$\sigma=\max \left\{\lambda_{\max }(\boldsymbol{P}), \frac{a}{2}\right\}$ 则选取‖ X(0),w(0)‖2≤γ,则V(0)≤σγ2,因此不等式(31)成立. 利用(30)和(31)式,可以推出
其中μ由(27)式定义,因此不等式(26)成立. 证毕.
-
系统(1)-(4)的模拟仿真
其中:
同时
我们令
可以验证矩阵A+BK是Hurwitz矩阵. 因此,系统满足(5)式,容易得到
其中:
则控制律为
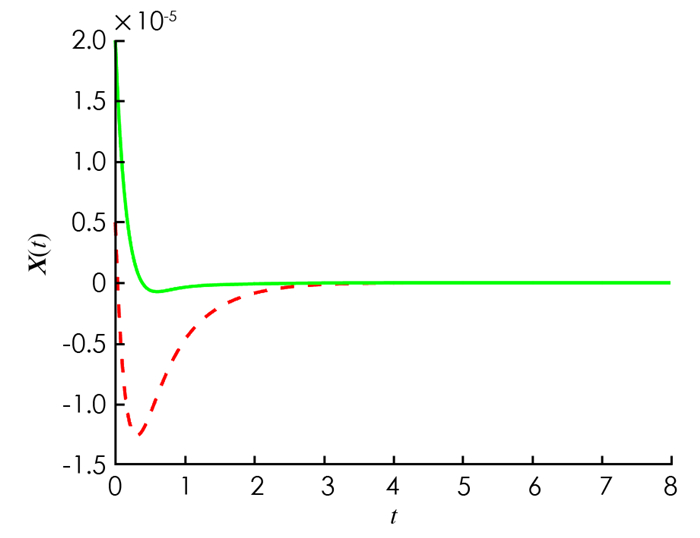
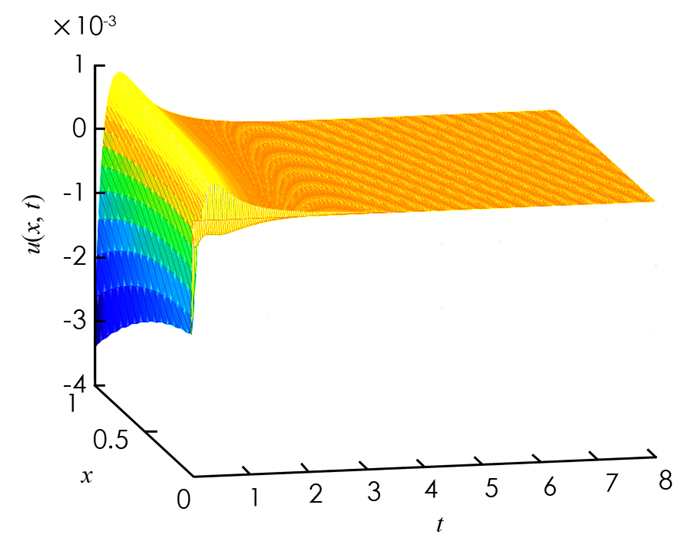
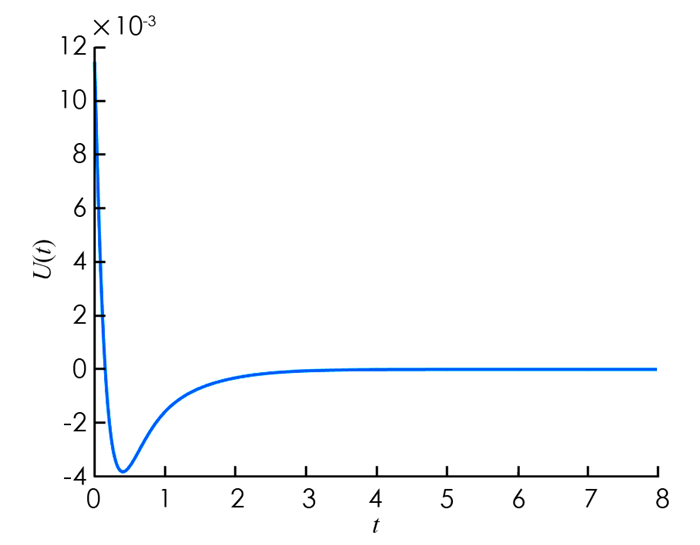
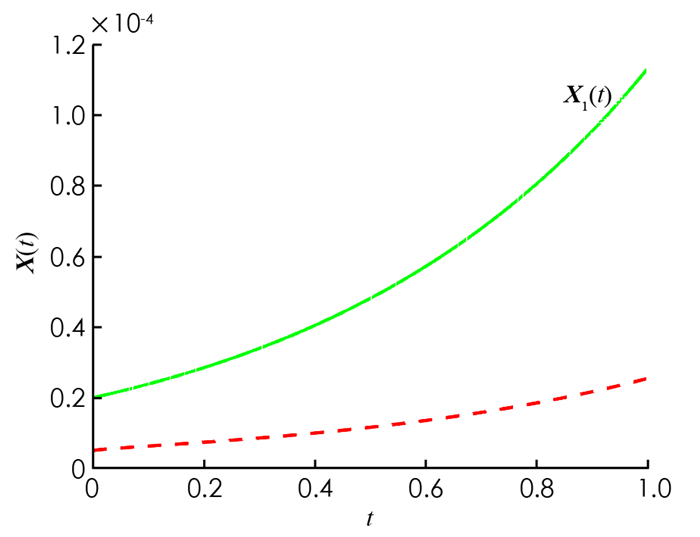
仿真结果见图 1-4. 图 1开环系统是不稳定的. 图 2和图 3显示在控制(32)输入下,闭环系统的信号在时间趋近于无穷时趋近于零. 图 4显示控制(32)是有界的.



 下载:
下载: