-
本文仅考虑有限无向的简单图.设G是有n个点的图. 若G的一个生成子图的每个分支是一个孤立点或者一条边,则称此生成子图为G的一个匹配.恰有k条边的匹配称为k-匹配.饱和了G的所有顶点的匹配称为G的完美匹配,图G的完美匹配的个数记为pm(G). 文献[1]定义了图G的匹配多项式为
这里W=(x,y),x和y分别是点和边的权重,p(G,k)是G的所有k-匹配的数目,且约定p(G,0)=1.假如令y=-1,我们便得到文献[2]中定义的匹配多项式
(1),(2)式互相确定,本文使用(2)式为图G的匹配多项式,并将μ(G,x)简记为μ(G). 匹配多项式在数学、统计物理和化学中都有很重要的应用.在统计物理领域,匹配多项式是描述一种物理系统的数学模型,首先由文献[3]引入.在理论化学领域,匹配多项式的根的绝对值之和称为该图的匹配能量,与这个图所表示的芳香烃的活性有关[4]. 匹配多项式的所有系数的绝对值之和(即所有匹配的总数)就是这个图表示的碳氢化合物的Hosoya指标,与这个化合物的沸点有关[5]. 匹配多项式是一种组合计数多项式,它与图的特征多项式、色多项式和其他多项式有许多联系[6-9].对于给定的图,计算这个图的匹配多项式是一个困难的问题,文献[10-13]计算了许多图的匹配多项式.关于Hosoya指标的研究可参见文献[14],关于匹配多项式对图的刻画的研究可参见文献[15-19].截至目前,还有许多基本图的匹配多项式仍然未知,如本文所涉及的柱面和Möbius带,这是两个较为基本的图,但其匹配多项式未知.作为对匹配多项式研究的补充,本文给出了这两个图的匹配多项式,并计算了这些图上的完美匹配的个数.
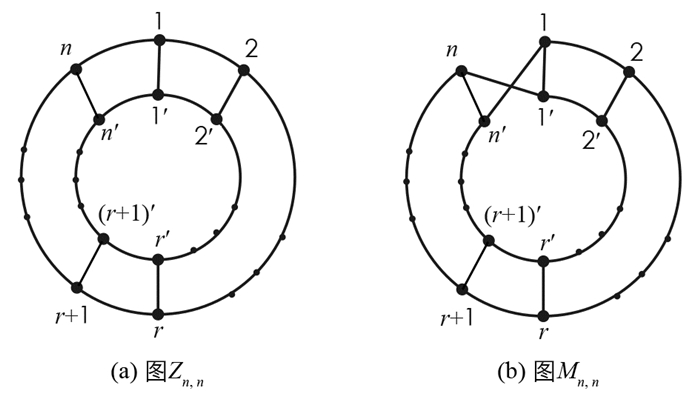
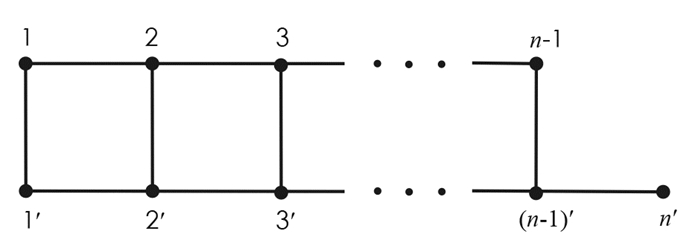
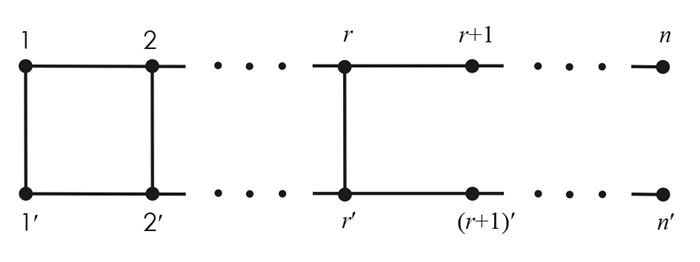
设G=(V(G),E(G))是一个简单图,V(G)是其顶点集,E(G)是其边集,其中E(G)的每一个元素是V(G)上的无序对,称为一条边.如果e∈E(G),以G\e表示从图G中删除边e后得到的图. 如果v∈V(G),以G\v表示删去点v以及与之相关联的所有边后得到的图.以Pn,Cn分别表示n个点的路、圈.给两条n个点的路,其顶点从左向右分别标记为1,2,…,n和1′,2′,…,n′,将这两条路上的点i和i′(i=1,2,…,r)分别用一条边连接,得到的图记为Ln,r(见图 1).把Ln,n称为梯子,简记为Ln.将图Ln,r的顶点1和n,1′和n′分别用一条边连接得到的图记为Zn,r,Zn,n称为柱面,简记为Zn.将图Ln,r的顶点1和n′,1′和n分别用一条边连接得到的图记为Mn,r,Mn,n称为Möbius带,记为Mn(见图 2).从梯子Ln中删去点n后得到的图记为Sn(见图 3).设G和H是两个点不交的图,定义图G和H的乘积图为G×H,其顶点集为V(G)×V(H),两个点(u1,v1),(u2,v2)∈V(G×H)在图G×H中邻接当且仅当u1=u2,v1与v2在图H中邻接,或u1与u2在G中邻接,v1=v2.于是,梯子Ln,n=Pn×P2,柱面图Zn,n=Cn×P2.
全文HTML
-
引理1[9] 设图G有k个连通分支:G1,G2,…,Gk,则
引理2[9] 设G是一个图,u∈V(G),e=uv∈E(G),则:
(ⅰ)
$\mu(G, x)=x \mu(G \backslash u, x)-\sum\limits_{i \sim u} \mu(G \backslash\{u, i\}, x)$ ;(ⅱ)
$\mu(G, x)=\mu(G \backslash e, x)-\mu(G \backslash\{u, v\}, x)$ .引理3[9]
引理4[14] 设G是有n个点的图,则
其中i是复数单位,i2=-1.
定理1
证 对Ln的边e=(n-1,n)、Sn的边e′=((n-1)′,n′)使用引理2,便得到(3)式的前两个式子.为了使(3)式的系数矩阵是一个方阵,我们填上第3个式子.
令(3)式的系数矩阵为
设矩阵A的特征多项式为
其中
$d_1=\mu\left(P_2\right)-1=x^2-2, d_2=-\mu\left(P_2\right)+2 \mu\left(P_1\right)^2-1=x^2, d_3=1$ .μ(Ln)满足递推关系式
初始条件为
因为(5)式的变量为t的生成函数
且
由生成函数的定义,定理1得证.
定理2
其中μ(L0,0)=1.
证 对Ln,r的边
$e_r=\left(r, r^{\prime}\right), e_{r-1}=\left(r-1, (r-1)^{\prime}\right), \cdots, e_1=\left(1, 1^{\prime}\right)$ 依次使用引理2(ⅱ),便得到下列式子:将以上各式相加,得到
定理3
其中Ln-1,0=2Pn-1.
证 对Zn,n的边
$e_n=\left(n, n^{\prime}\right), e_{n-1}=\left(n-1, (n-1)^{\prime}\right), \cdots, e_1=\left(1, 1^{\prime}\right)$ 依次使用引理2(ⅱ),便得到下列式子:相加上面各式,定理3得证.
定理4
其中Ln-1,0=2Pn-1.
证 对Mn,n的边
$e_n=\left(n, n^{\prime}\right), e_{n-1}=\left(n-1, (n-1)^{\prime}\right), \cdots, e_1=\left(1, 1^{\prime}\right)$ 依次使用引理2(ⅱ),便得到下列式子:相加上面各式,定理4得证.
推论1 (ⅰ)
$\mu\left(M_{n, n}\right)-\mu\left(Z_{n, n}\right)=\mu\left(C_{2 n}\right)-\mu\left(C_n\right)^2$ ;(ⅱ)
(ⅲ)
$Z\left(M_{n, n}\right)-Z\left(Z_{n, n}\right)=Z\left(C_{2 n}\right)-Z\left(C_n\right)^2$ .证 由定理3和定理4,(ⅰ)显然.
(ⅱ)由匹配多项式的定义知
由(ⅰ)和引理3知
当n为奇数时,
$(-1)^n\left(\mu\left(C_{2 n}, 0\right)-\mu\left(C_n, 0\right)^2\right)=(-1)^n\left((-1)^n \times 2-0\right)=2$ .当n为偶数时,
$(-1)^n\left(\mu\left(C_{2 n}, 0\right)-\mu\left(C_n, 0\right)^2\right)=(-1)^n\left((-1)^n \times 2-\left((-1)^{\frac{n}{2}} \times 2\right)^2\right)=-2$ .(ⅲ)由引理4和(ⅰ)知
推论1得证.
-
推论2
证 在定理1中令k2=0,x=0,便得该表达式的常数项为
由于Ln的完美匹配数pm(Ln)等于多项式μ(Ln,x)的常数项乘(-1)n,于是
注1 很容易计算Ln的完美匹配数就是著名的斐波那契数,其前几项的值L1,L2,L3,L4的完美匹配数分别为1,2,3,5,与推论2计算的值是吻合的.推论2给出了斐波那契数的另外一种表示法.
推论3 (ⅰ) 当n为偶数时,
(ⅱ) 当n为奇数时,
证 众所周知,当n=4m或n=4m+2时,路Pn的匹配多项式的常数项为1或-1;当n为奇数时,路Pn的匹配多项式的常数项均为0.令x=0,便得:
当n为偶数时,定理2中表达式的常数项为
于是
当n为奇数时,定理2中表达式的常数项为
推论4 (ⅰ) 当n为偶数时,
(ⅱ) 当n为奇数时,
证 众所周知,当n=4m或n=4m+2时,圈Cn的匹配多项式的常数项为2或-2;当n为奇数时,圈Cn的匹配多项式的常数项均为0,令x=0,便得:
当n为偶数时,由推论3知,定理3中表达式的常数项为
当n为奇数时,定理3中表达式的常数项为
注2容易验证图Z3和Z4的完美匹配数分别为4和9,与推论4计算的值是吻合的.
推论5 (ⅰ) 当n为偶数时,
(ⅱ) 当n为奇数时,
证 令x=0,便得:
当n为偶数时,由推论3知,定理4中表达式的常数项为
当n为奇数时,定理4中表达式的常数项为
注3 容易验证图M3和M4的完美匹配数分别为6和7,与推论5计算的值是吻合的.



 下载:
下载: