-
由导体外磁信号重建导体内部电源分布是磁异常探测关键算法,被广泛应用于地球物理、生物医学、低频通信、基础设施安全检查和资源勘探等领域[1].它可采用麦克斯韦逆向方程进行求解,但其结果是不适定的,须在满足条件的解集中施加限制条件而获取合理的数值解.逆向方程常见的解析方法包括最小范数解、加权最小范数解、迭代算法和最大熵算法等[2].最小范数解是基于Moore-Penrose广义逆的线性方程组解,通常采用奇异值分解算法来求解广义逆[3-4];加权最小范数解是使用一个加权矩阵,在满足方程解集中,寻找一个解使其加权范数为最小[5].这两种方法不断优化取舍奇异值,可降低噪声影响并减少有用信息丢失,但可能会遇到解的不稳定性问题,造成解对测量误差值过分敏感.迭代算法不断用假定解集递推实测数值,通过最小化两者误差逐步接近信号解析源的最可能值.当测量结果存在误差时,迭代过程收敛到局域最小值就成了难题,且该算法对于实时求解计算效率具有很高要求[6].最大熵算法在满足方程的解集中,要求该解满足一个熵函数为最大,它可提高分辨率并抑制噪声[7].该算法最主要的问题是存在非线性,对解析结果难以做出定量分析,数值解析过程复杂且计算耗时长.
逆向求解方程可采用点源矢量作为一种限制条件,由于不设重构网格,因而无需固定点源矢量空间位置,因此这种信号增益矩阵是未知的,其信号方程对应于一个非线性方程组.对于基于点源矢量逆向求解方程解析方法的基本思想是确定一个目标函数,寻找一组点源矢量,使其目标函数达到最小,其本质是将目标函数转化为非线性最小优化问题[8].目前大多数逆向求解方程解析方法计算量大,极为耗时,且信号解析源定位精度有待提高.本研究提出一例逆向求解方程的解析方法,可用于求解信号解析源测量数据所对应的点源矢量,其本质是一种基于傅里叶变换的数值解析方法,计算过程无需迭代计算,从而降低了对计算手段效率的要求.
全文HTML
-
点源矢量包含了两个符号相反且大小相等IF的单极子(源/汇),两个单极子之间存在极微距离d所分隔,因此,点源矢量数学模型应满足下列条件:d→0
其中:p为有限值,量p称为点源矢量极矩即点源矢量大小.
单个点源矢量是一个矢量,其方向定义为由汇指向源.若定义d是由汇到源的位移,而Sd是该方向上单位矢量,则点源矢量大小p可表述为:
点源矢量数学模型可表示为局域中一个微小线性电流,具有安培米量纲,量化值为点源矢量极矩,是电流强度与电流线度的乘积,在数学建模中通常被处理为点源.本逆向求解方程解析方法采用点源矢量数学模型模拟单电流源,点源矢量矩就是局域电流与流动方向上电流线度的乘积.
-
麦克斯韦方程组用于描述电磁场信号源分布的数学模型[9],对于准静态近似条件即在非导电非磁性同类空间,则有:
由(3)式可知,电磁场信号解析源外任意点准静态电流产生的磁场可表述为毕奥-萨伐尔(Biot-savart)定律,即[10]:
式中:C为电磁场信号解析源内部电导率分块连续的有界导体;B(r)为C外部的测量磁场;P为电流密度向量,表现为原在电流密度与欧姆电流密度之和;μ=4π×10-7 H/m为真空中磁介电常数;r为空间观测点坐标矢量,r ′为电磁场信号解析源坐标矢量.
逆向求解方程解析是指利用电磁场信号解析源外部电磁场数据推断信号解析源内部电流分布,根据毕奥-萨伐尔定律可知电流密度分布与其产生磁场之间的相互关系.这里以单电流源点源矢量数学模型作为信号解析源,其坐标为R ′=(x′,y′,z′),则逆向求解方程可表述为:
式中:G (R)为格林函数,P也被称为点源矢量极矩矢量,R是信号解析源到观测点的径矢量.
若已知径矢量R,则(6)式和(7)式可求解出前向求解方程,即已知点源矢量信号解析源参数可计算出空间任意点磁感应矢量值及其空间导数.反之,(6)式和(7)式可用于解析逆向求解方程,即已知电磁场信号空间分布,可反演推算出信号解析源参数包括点源矢量位置和强度.
-
超导量子干涉器(superconducting quantum interfere device,SQUID)梯度计所测磁场分布为全张量信号[11],本解析方法是基于磁感应强度电压信号的一阶梯度.假定Ψ为任一观测点,对应空间坐标系中的坐标矢量为r =(rx,ry,rz),其磁感应强度电压信号矢量(以下简称磁强矢量)和重力矢量分别为:
磁强矢量和重力矢量一阶梯度矩阵分别为:
如果观测点Ψ位于同类非电导非磁性的介质空间,那么:
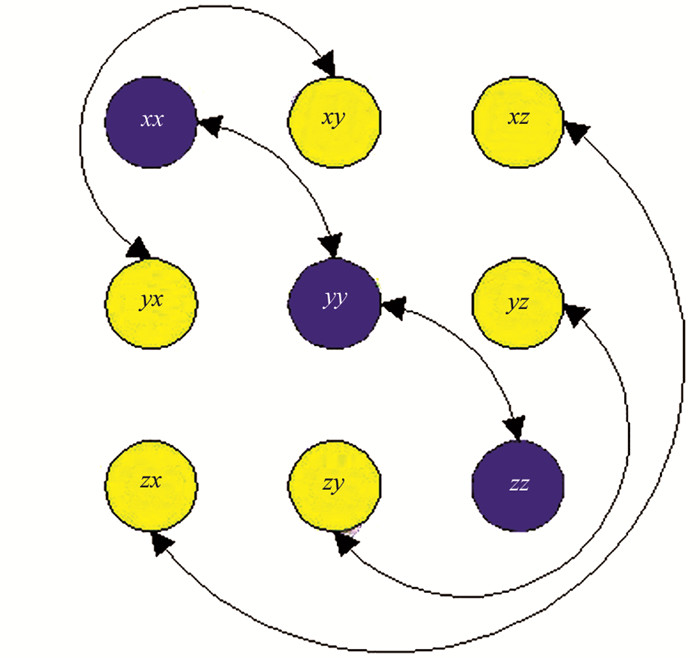
D 1和Γ 1是两个张量对称矩阵,它们中5个元素是相互独立的,图 1为两个矩阵中张量元素分布图.
当观测点到电流点源矢量之间距离(r)远大于其空间尺寸(r′)时,便可得到:
其中:MB和MG分别是点源矢量磁矩和重力磁矩.由(16)式和(17)式可见,磁强矢量和重力矢量对于空间坐标r=(rx,ry,rz)具有等价关系.根据欧拉线性关系可知:
由于矩阵D1是正交矩阵,其特征值为λ1,λ2,λ3,对于不同的磁异常信号解析源,其特征值是不一样的,由(10)~(19)式可将λ1,λ2和λ3与坐标r=(rx,ry,rz)建立关系,从而可推导出电流点源矢量位置信息.
-
对(4)式扩展向量积,则可知磁感应分量如Bx有:
式中:SQUID传感器观测平面平行于笛卡尔坐标系XOY平面且z=Z0.
对(20)式左、右两侧同时进行双傅里叶变换,则有:
对式(21)进行傅里叶逆变换有:
(21) 式、(22)式中f(x,y,z)和F(kx,ky,z)分别是坐标函数和其傅里叶成像,kx和ky为波向量k的分量.根据卷积定律可知,(20)式中点源矢量和磁感应向量分量相互关系为:
式中:bx(kx,ky,z0)=F [Bx]和Py(kx,ky)=F [Py]分别为磁感应向量分量和点源矢量的傅里叶成像;g(kx,ky,z0)为格林函数g(x-x′,y-y′,z0)=g(r)的傅里叶成像.
(24) 式傅里叶变换后可得格林函数傅里叶成像:
式中:
$ k = \sqrt {(k_x^2 + k_y^2)} $ 为传播向量幅值.与上述推导相同,对(4)式扩展向量积和傅里叶变换,则波平面磁感应向量其他分量傅里叶成像有:由连续电流方程div(P)=0以及对波平面进行双傅里叶积分变换,可知:
波平面中点源矢量向量中分量为:
若已知磁感应向量Bz分量和Z0,则在xyz坐标系中经傅里叶逆变换计算出点源矢量2个分量值.
3.1. 点源矢量位置解析算法
3.2. 点源矢量强度解析算法
-
逆向求解方程模拟仿真试验是以所测磁场信号作为磁源对象信息特征载体,这里假定模拟磁源研究对象位于同态磁场中,其磁感应强度矢量是顺着直角坐标系oz轴方向,oz轴方向与观测平面标准方向相一致. SQUID梯度计被用于测量每个观测点的磁场信号,每个观测点磁场信号记录时间为60 s.模拟磁源研究对象和梯度计相互位置确定方案为:SQUID梯度计线圈几何中心点投影至xoy测量平面上,应尽可能靠近模拟磁源研究对象的剖面中心线,最理想状况是与中心线重合. SQUID梯度计沿着ox轴或oy轴进行移动,每个观测点第一阶段前30 s向前移动,第二阶段后30 s向后移动.
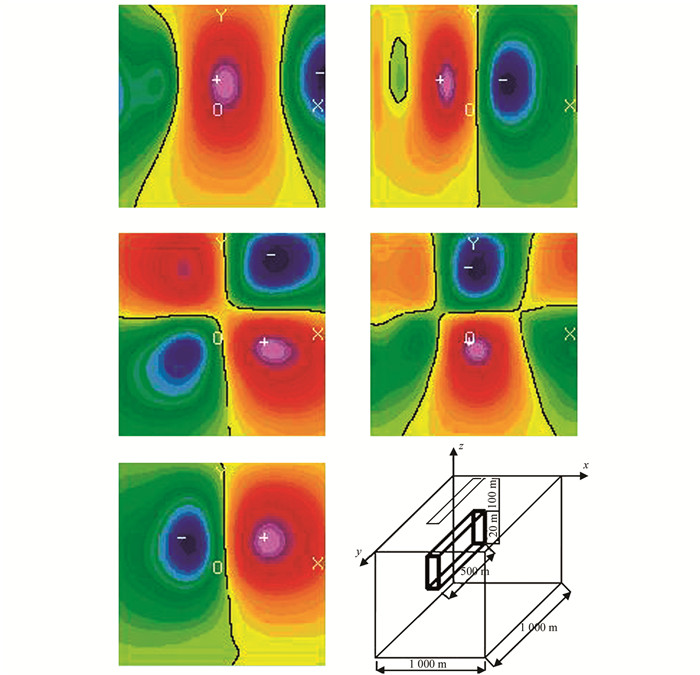
观测点是平面坐标系中31×31相互正交网格节点,相邻节点步距均为3.33 m,平面观测范围为1 000 m.从物体几何中心到观测平面距离(即物体深度)为100 m,计算出每个观测点SQUID梯度计输出信号的一阶梯度(∂Bz/∂z).长方体模拟信号源空间形状及其观测平面见图 2右下角,并采用最大熵算法[6]与本文所述算法同时进行模拟对比分析,两种解析方法逆向求解长方体模拟磁源均是在Windows XP操作系统下,利用Visual C++开发平台编程实现数值计算,模拟磁源研究对象信息特征是以磁源外所测磁场信号的一阶梯度来表示,并以等磁场分布图形式进行显示,包括磁感应强度矢量所有一阶梯度分量分布(图 2).
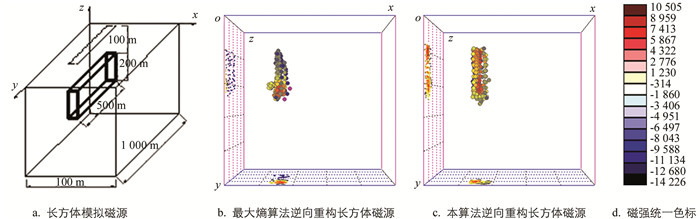
由于长方体模拟磁源位置和空间形态是已知的,故可换算出其每一个观测点上磁感应强度矢量及其一阶梯度准确数值. 图 3为长方体模拟磁源的逆向重构结果,其结果是以N个点源矢量组合形式呈现,其中长方体距离观测平面均为100 m,长方体(x,y)坐标分别为(-300,-300),长方体在x,y,z轴方向长度分别为20 m×500 m×200 m.长方体模拟磁源逆向求解方程解析结果显示最大磁感应信号强度显著大于其最小值(图 3b和图 3c),N个不同点源矢量集中在一个区域里形似长方体状.将长方体模拟磁源与上述两种算法逆向重构结果进行误差对比分析,其信息误差率计算方法为:
其中:sxoz,sxoy,syoz分别为长方体磁源逆向重构结果在xoz平面、xoy平面和yoz平面的投影轮廓线面积.本算法和最大熵算法的信息误差率分别为2.68%和11.7%.此外,本算法和最大熵算法逆向求解过程分别耗时约2 s和6 s(均在惠普工作站HP xw8400中执行计算).
-
本逆向求解方程解析方法是通过点源矢量信号解析源外部磁场分布数据来逆向求解点源矢量信号解析源信息,其本质是将信号解析源分解成一定数量的独立点源矢量,分别通过两个解析算法求解出点源矢量位置和强度变化信息.点源矢量物理意义表现为:受电荷守恒的约束,不可能找到一个孤立的单极电流源.但同时有正有负且满足总量为零的单电流源在现实中是可以实现.其中,最简单且又可反映单电源特点的正-负单源组合即为点源矢量.点源矢量本质上也非真实单电流源模型,但比单极子更有价值.由于逆向求解方程不存在唯一解,可限定电流密度向量分布于二维平面中[12],这种方法也适用于点源矢量信号解析源数学模型.因此,点源矢量位置解析算法和点源矢量强度解析算法都是基于SQUID传感器测量平面平行于笛卡尔坐标系xoy平面的假设.目前,SQUID传感器是已知灵敏度(10-15 T)最高的弱磁信号探测器件,被广泛应用于磁异常信号探测领域如军事探潜等[13],本文所述逆向求解方程解析方法可集成于SQUID弱磁探测软件系统中,主要应用于弱磁目标检测与定位.此外,点源矢量强度解析算法只需提供磁测信号中磁感应向量z轴方向分量Bz参见式(22),无需测量x轴、y轴方向分量.
点源矢量位置解析算法首先通过构造磁强矢量和重力矢量一阶梯度,其次对一阶梯度正交矩阵求解矩阵特征值,最后通过欧拉线性关系可建立特征值与点源矢量坐标关系式,以获取点源矢量位置.点源矢量强度解析算法则首先利用引导场概念建立磁通量与点源矢量信号解析源模型之间的关系式,其次将准静态条件下点源矢量磁场信号微分方程(散度和旋度)通过双傅里叶变换,转化为傅氏空间的卷积分求和方程,再引入格林函数和波平面方法获得傅氏空间方程解,最后再施以傅里叶逆变换,获得点源矢量信号解析源的空间分布.该算法优势在于不对点源矢量模型位置施加限制,可分布于信号解析源平面任意位置(图 3),且无需迭代计算或非线性优化过程,从而显著地减少计算时间,其局限在于只能求解平面上的点源矢量信号解析源模型数据分布.
最大熵算法逆向重构出的长方体磁源外形呈非中心轴(x轴和y轴)对称(图 3b),相比而言本文所述算法逆向重构出的长方体磁源外形呈中心轴(x轴和y轴)对称(图 3c),且投射至xoy平面、yoz平面形状更接近于矩形,因此,本文所述算法逆向重构出的长方体外形更加优于最大熵算法.此外,本算法信息误差率(2.68%)不高于3%,符合信息准确度要求,而最大熵算法信息误差率为11.7%,不符合信息准确度要求.且在相同软硬件平台下,本文所述算法逆向重构速度(约2 s)比最大熵算法逆向速度(约6 s)更快.综上可见,在相同条件下,本文所述逆向求解方程解析方法性能显著优于最大熵算法.
-
本研究首先引入点源矢量数学模型,并基于点源矢量数学模型构建了电磁场空间分布测量数据的逆向求解方程数学模型;其次,针对点源矢量位置和点源矢量强度分别提出对应的解析算法;最后,利用数值模拟对比试验逆向重构出长方体磁源分布,试验结果表明了所述逆向求解方程解析方法的准确度和可靠性,且本算法逆向重构效果显著优于最大熵算法.



 下载:
下载: