-
开放科学(资源服务)标识码(OSID):

-
标记歧义问题[1-2]是当前机器学习和数据挖掘[3-4]领域中备受关注的热门话题. 单标记学习(Single-Label Learning,SLL)[5]和多标记学习(Multi-Label Learning,MLL)[6-8]是当前处理标记歧义问题的2种成熟的学习范式. 单标记学习假设每个样本只能与一种逻辑标记相关联,拥有该标记则为1,否则为0. 而多标记学习则假设每个样本能与一组逻辑标记相关联. 尽管多标记学习相比于单标记学习能够解决更复杂的标记歧义问题,但是这2种学习范式都只能回答标记是否属于一个样本,而无法回答标记对样本的描述程度. 为了解决这一问题,Geng等人[9]提出了标记分布学习(Label Distribution Learning,LDL). 该学习范式为每个样本分配一组描述度,并假设所有标记的描述度之和为1. 这种学习范式能够准确区分标记对于样本的描述度差异,可适用于更加广泛的应用场景.
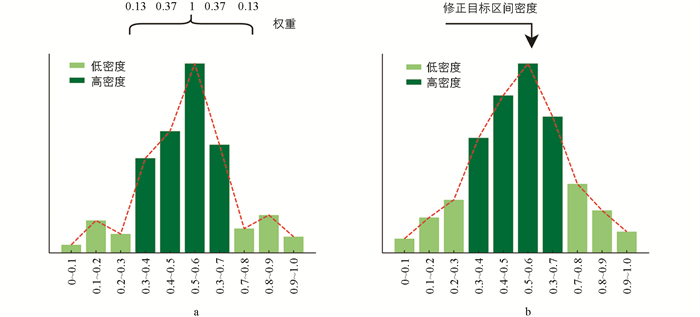
现有的LDL算法已经应用了多种方法来提高预测性能. 最初,LDLLC[10]通过应用全局标记相关性来扩展特征空间以提高性能. 随后,LDL-SCL[11]、LDL-FLC[12]建议利用局部标记相关性以提升性能. 最后,LDL-LDM[13]提出了同时利用局部和全局标记相关性的方法. 除了利用标记相关性之外,LDL-HR[14]提议首先学习描述度最高的标记,然后学习其他标记,以避免目标不匹配. 而LDLSF[15]则提出了一种为每个标记选择特定特征的方法,而不是共享所有特征. 然而,这些算法都是在假设训练集是均匀分布的前提下构建的. 而在实际应用中,情况往往并非如此. 一种标记所对应的训练样本的分布通常是非均匀分布的,如图 1所示,其中横坐标表示描述度区间,纵坐标表示在该区间内样本的数量,浅绿色为低密度区域,深绿色为高密度区域. 作为一种数据驱动的学习范式,在使用非均匀数据时往往会忽略来自低密度区域的样本,从而导致预测出现错误[16-18].
为了处理非均匀分布数据,本文提出了一种新的基于代价敏感的标记分布学习算法(Cost-Sensitive Method for Label Distribution Learning,CSLDL). 我们根据样本的密度构建代价矩阵[19],并用它来对传统的K-L散度目标函数进行优化,使其适用于非均匀分布数据. 首先,将描述度集等分为多个区间,并为每一种标记分别统计其在这些区间中样本的经验密度. 标记分布数据作为一种连续型数据,同一种标记的相邻描述度之间不存在严格的界限[20-21]. 然而,在划分子区间之后,会破坏相邻区间之间的连续性. 为了重构相邻区间之间的连续性,我们利用邻居对经验密度进行修正,使其不仅考虑当前区间的经验密度,还要考虑邻居区间的经验密度. 例如,区间同时考虑了自身和邻居的经验密度,其中设置贡献权重以考虑与目标区间的距离,距离越远权重越小. 修正后,不仅重建了相邻区间的连续性,还得到了更加平滑的分布,如图 1(b)所示. 在现实生活中,连续性数据的变化应该是平滑的,例如人口统计数据,正常情况下,每年的人口只会小幅度增加或减少. 修正后的密度分布也变得更加平滑,可以更好地反映现实世界数据的真实情况,从而增加算法的泛化性. 最后,利用平滑后的密度信息构建代价矩阵,并用它对传统的K-L散度目标函数进行改造,对处于高密度区域的样本设置较小的代价,反之设置较大的代价.
为了验证本文提出的CSLDL方法,我们对多个数据集进行了广泛的实验. 实验结果表明,与6种先进的方法相比,CSLDL预测的结果最贴近真实数据. 本文的主要贡献包括3个方面:①提出了一种代价敏感的标记分布学习算法(CSLDL),通过样本密度信息以更均衡的方式处理模型对高密度区域样本的偏重;②通过利用近邻修正目标区间的经验密度,不仅重建了相邻区间的连续性,而且得到了更符合现实规律的分布数据;③应用不同数据集的实验结果证明了提出的算法的有效性和优越性.
全文HTML
-
令X=[x1;x2;…;xn]∈Rn×q表示输入特征空间,Y={y1,y2,…,yo}表示标记集合,D=[d1;d2;…;dn]∈[0, 1]n×o表示与输入空间相对应的标记空间. 其中,n为样本数量,q为特征维度,o为标记数量. 第i个样本表示为xi∈X,其第j个标记的描述度表示为dij. 每个样本的描述度应满足
-
当前常见的标记学习算法设计主要基于以下3种策略[22]:
1) 问题转化(Problem Transformation,PT):这种策略将标记分布学习问题转化为单标记学习问题. 具体而言,训练样本被转化为加权的单标记样本,权重可以由标记的描述度得到,转化后的样本就可以使用单标记学习算法进行处理. 基于此策略的代表算法有PT-Bayes和PT-SVM等.
2) 算法改造(Algorithm Adaptation,AA):这种策略将传统单标记或多标记学习算法改造为能够处理标记分布问题的算法. 该策略的代表算法有基于k近邻改造的AA-kNN算法以及基于反向传播改造的AA-BP算法.
3) 专用算法(Specialized Algorithm,SA):这种策略是根据标记分布学习本身固有特性设计的专用算法. 专用算法通常由3个模块组成,包括输出模型、目标函数和优化方法. 现有的专用算法大多采用K-L散度作为目标函数,并假设所有标记的贡献相等来进行模型优化. 然而在实际应用中,训练数据通常呈现不均匀分布,使用传统K-L散度为目标函数训练的模型会忽略来自低密度区域的样本. 为了解决这个问题,本文提出了一种基于代价敏感的标记分布学习算法,该算法利用样本的密度信息来平衡模型对高密度区域样本的偏重.
1.1. 符号系统
1.2. 标记分布学习算法
-
为了平衡传统模型对高密度区域样本的偏重,本文采用了对高密度区域样本设置较小代价、对低密度区域样本设置较大代价的方法. 为了满足这一需求,我们使用样本密度的倒数或开方后的倒数作为代价. 经过实验验证,后者的效果更好. 需要注意的是,不同标记所对应的样本分布是不同的,因此每种标记都有一个对应的代价向量.
首先,将[0, 1]划分为m个子区间s1,s2,…,sm,每个区间拥有相同的间隔
$\frac{1}{m}$ ,即$s_{1}=\left[0, \frac{1}{m}\right), s_{2}=$ $\left[\frac{1}{m}, \frac{2}{m}\right), \cdots, s_{m}=\left[1-\frac{1}{m}, 1\right]$ ,并统计标记yj在这些子区间的样本密度,从而得到其对应的代价向量:其中:cjb表示区间sb样本密度开方后的倒数.
根据标记分布数据的特点,同一标记的相邻描述度之间不存在严格的界限,而是呈现连续性. 然而,对子区间的划分却在相邻区间之间引入了分界线,从而破坏了它们之间的连续性. 为了重新建立相邻区间之间的连续性,本文采用核函数来提取相邻区间的信息,以保持数据的连续性.
其中:h表示考虑的左右邻居数量,核函数为对称核函数,满足
$k(i, b)=k(b, i)$ 以及$\nabla_{i} k(i, b)+$ $\nabla_{b} k(b, i)=0$ . 常见的对称核函数有高斯核、拉普拉斯核等,本文采用拉普拉斯核.考虑了近邻信息后,不仅能够重建不同区域之间的连续性,还能使样本分布更加平滑,更符合真实分布,从而提高算法的泛化能力.
为了方便计算,结合代价向量和训练数据的标记空间构建n×o的代价矩阵:
其中:
$a_{i j}=\hat{c}_{j b}$ ,仅当样本xi的第j个标记dij位于区域sb时. -
基于代价敏感的标记分布学习算法(CSLDL)符合专用算法设计策略,由输出模型、目标函数、以及优化方法构成.
标记yj对样本xi的描述度由条件概率的形式表示,其参数模型记作p(yj|xi;θ). 本文采用最大熵模型作为输出模型
其中:
$Z=\sum\limits_{j} \exp \left(\sum\limits_{k} \theta_{j, k} x_{i k}\right)$ 为归一化项,保证xi所有标记的描述度之和为1;θ是描述特征与标记分布之间关系的系数矩阵,θj,k是θ中的一个元素;xik是xi的第k个特征.为了获取最优参数θ,构建如下目标函数:
其中:L(θ)为定义在训练数据上的损失函数,Ω(θ)为约束模型参数复杂度的正则项,λ控制正则的贡献度.
损失函数用于度量真实标记分布与预测标记分布之间的相似性,常见的损失函数有欧式距离,K-L散度等. 经过实验验证,采用K-L散度效果最佳,
其中:dij为标记yj对样本xi的真实描述度,p(yj|xi;θ)为预测描述度.
传统的K-L散度无法平衡模型对高密度区域样本的偏重,因此本文将其与代价矩阵相结合以平衡这种偏重. 结合代价矩阵的损失函数表示为
本文采用标记分布学习中常用的L2范数来约束模型参数θ,以防止模型过拟合,即:
将公式(8)和公式(9)代入公式(6),最终目标函数表示为
-
本文采用拟牛顿法(limited-memory quasi-Newton method,L-BFGS)[23]对目标函数T(θ)进行求解. 对应当前迭代次数的二阶泰勒展开为
其中:
$\varDelta=\left(\boldsymbol{\theta}^{(l+1)}-\boldsymbol{\theta}^{(l)}\right)$ 为参数变化量,$\nabla T\left(\boldsymbol{\theta}^{(l)}\right)$ 为梯度矩阵,$H\left(\boldsymbol{\theta}^{(l)}\right)$ 是Hessian矩阵.式(11)最小化可得
在L-BFGS优化方法中,Δ(l)被视为搜索方向,选择满足Wolfe准则的α(l)作为步长,则θ的迭代公式为
L-BFGS的基本思想是避免直接计算牛顿法中使用的逆Hessian矩阵,而用迭代更新的矩阵B来近似逆Hessian矩阵,其表示为
其中:I是单位矩阵,其余变量如下表示
对于目标函数T(θ)的优化,L-BFGS的计算主要与其一阶梯度有关,表示为
得到最佳参数θ*之后,代入公式(5)求得样本标记分布.
2.1. 代价矩阵
2.2. 标记分布学习
2.3. 优化
-
M2B[24]是由Ren等人基于面部美感感知的原始数据集[25]整理而来,其标记分布通过k-wise模型转化得到. Emotion6[26]包含1 980张来自Flickr的图像,用于情绪预测研究. 该数据集通过投票标注了7种情绪类别(愤怒、厌恶、喜悦、恐惧、悲伤、惊讶和中性),并通过文献[15]中提出的方法为每张图像提取了一个168维的特征向量. Movie[9]是一个计算电影用户评分的数据集,使用478 656位用户对7 755部电影的54 242 292次评分作为数据源. 数据来自Netflix,评分范围从1~5(5种标记). 电影的标记分布为每个评级级别的百分比,电影的特征是从流派、导演、演员、国家、预算等数据中提取的,每部电影的特征向量是1 869维. Flickr-LDL和Twitter-LDL[27]分别包含11 150和10 045张图像,其标记为8种情感(愤怒、开心、敬畏、满足、厌恶、兴奋、恐惧和悲伤). 按照文献[15]中提出的方法,分别使用HOG[28]和Color Moment[29]对2个数据集提取特征向量,然后使用PCA将特征降维到168维. Natural-Scene[9]来自2 000个自然场景图像. FBP5500[30]来自5 500张彩色人脸照片. 最后3个数据集Yeast-cdc、Yeast-cold和Yeast-spoem[31]是从酵母的真实生物学实验中获得的. 表 1中给出了这些数据集的一些基本统计数据.
-
标记分布学习的评价指标可以划分为2种,分别为距离指标和相似度指标[32]. 常见的距离指标包括Chebyshev距离↓、Squared χ2距离↓、Euclidean距离↓以及Sφrensen距离↓,常见的相似度指标有Cosine相关系数↑和Fidelity相似度↑. ↓表示评价指标度量值越低性能越好,↑表示评价指标度量值越高性能越好. 由于同类型指标的实验结果是相似的,为了文章排版的便利性,本文在两类指标中各选取部分指标(Sφrensen、Fidelity)来展示实验结果.
-
CSLDL与其他6种先进的算法进行比较,包括PT-Bayes[9]、AA-kNN[9]、SA-BFGS[33]、LDL-LDM[13]、LDL-HR[14]以及LDL-SF[15]. 本文对比实验参数与原文中的参数设置一致. 具体来说,对于AA-kNN,邻居数量k设置为5. 对于SA-BFGS,c1=10-4,c2=0.9. 对于LDL-HR,λ1=0.001,λ2和λ3选自{10-3,…,1},ρ=0.01. 对于LDL-LDM,λ1、λ2和λ3选自{10-3,…,103},g选自{1,2,3,…,14}. 对于LDL-SF,参数λ1、λ2和λ3选自{10-6,10-5,…,10-1},ρ=10-3.
-
为了验证CSLDL的有效性,我们进行了一项涉及以下4个实验的消融研究(ablation study,AS):
(a) 不考虑代价敏感,且不使用正则项;
(b) 考虑代价敏感,但不使用邻居修正和正则项;
(c) 考虑代价敏感,并使用邻居修正,但不使用正则项;
(d) 考虑代价敏感,并使用邻居修正和正则项.
为了进行公平的比较,将m固定为10,h固定为1,λ固定为0.1. 实验结果如表 2所示,在考虑代价敏感后,如果不进行邻居修正,可能会降低预测性能(a→b),反之可以得到更好的效果(a→c),并且在加入正则项后可以得到进一步提升(c→d). 这证明了CSLDL算法的有效性.
-
本文的主要参数有子区间的数量m,左右邻居数量h以及正则项贡献度λ. 为了方便排版,仅对部分数据集的表现进行了报告.
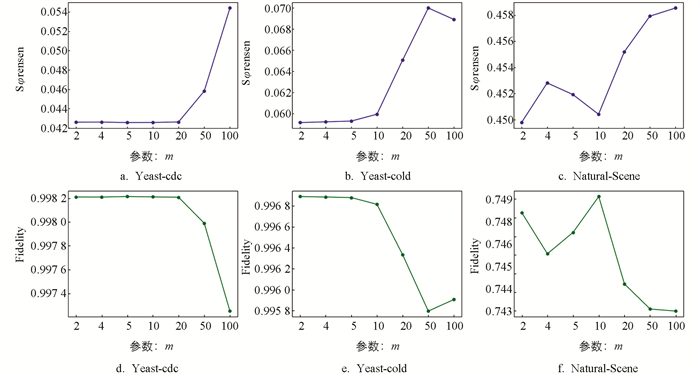
首先将h固定为1,λ固定为0.1,m依次设置为{2,4,5,10,20,50,100}. 如图 2所示,可以观察到当m=10时,3个数据集在2种指标之下都能取得较好的结果.
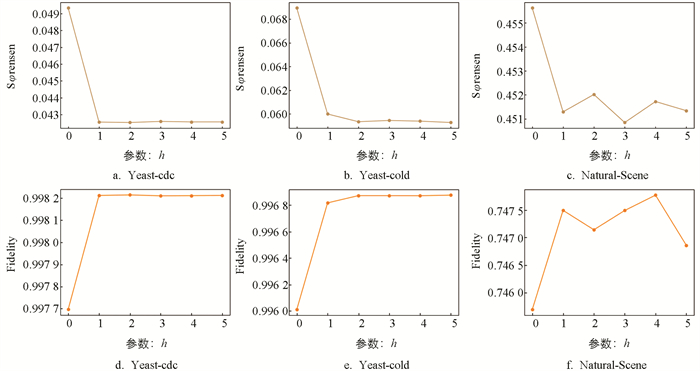
将参数m固定为10,λ固定为0.1,h依次设置为{0,1,2,3,4,5}. 实验结果如图 3所示,当利用邻居进行密度修正后,效果显著提升(h=0→h=1);当h≥2时,实验结果只在很小范围内变化.
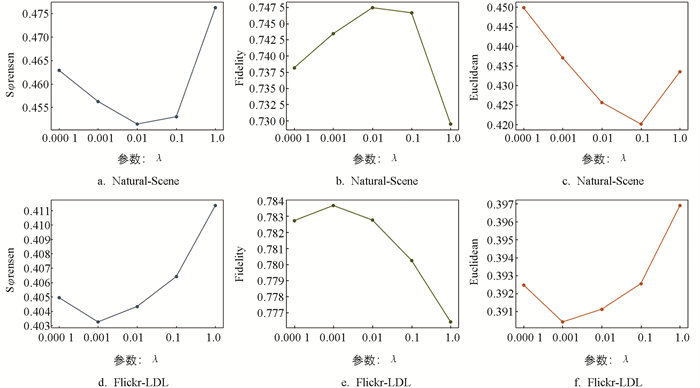
将参数m固定为10,h固定为2,λ依次设置为{0.000 1,0.001,0.01,0.1,1}. 实验结果如图 4所示,当λ等于0.001或者0.01时,效果最好. 综上所述,对所有数据集,参数设置如下,m=10,h=2,λ选自{0.001,0.01}.
-
本文采用十折交叉验证的方法,将训练数据随机划分为10份,每次选取其中9份用作训练集,1份作为测试集. 该过程被重复执行10次,并记录下数据集中每种算法排名的平均值和标准差,以确保评估结果的可靠性. 实验结果如表 3~4所示,其中黑体数字表示在当前数据集下,该算法表现最佳. 通过对7种算法在所有数据集下的表现进行平均排名,可以清晰地看出CSLDL算法的有效性和优越性.
3.1. 数据集
3.2. 评价指标
3.3. 实验设置
3.4. 消融实验
3.5. 参数优化
3.6. 实验结果
-
标记分布学习展现出了强大的泛化能力,相较于单标记学习和多标记学习,它可以更有效地应对标记歧义问题. 然而,现有的标记分布学习算法主要是针对均匀分布数据而设计的,却常忽视了实际情况下训练数据中普遍存在的不均匀分布现象. 本文提出了一种基于代价敏感的标记分布学习算法,旨在处理非均匀分布数据. 实验结果表明,CSLDL算法在处理这类数据时表现优于大多数现有的标记分布学习算法.
在未来的工作中,我们将尝试探索其他方法来处理非均匀分布数据,以取得更加高效的结果. 例如,可以考虑将数据合成、进行重采样等方法迁移到标记分布学习领域;也可以对原始数据进行增强处理,使其更容易被标记所描述等.



 下载:
下载: