-
电弱统一标准模型(the electroweak standard model,SM)是20世纪粒子物理学中颇具影响的唯象理论之一,在描述电磁与弱相互作用中取得了巨大成功,被标准模型预言的基本粒子都已经得到了实验数据的支持与验证,尤其是2012年人们用大型强子对撞机发现了标准模型预言的Higgs玻色子. 自标准模型提出以来,国际上出现许多相关理论研究工作,其中涉及“精确”检验标准模型的理论计算工作一直备受学术界关注,而这些理论计算工作本身也对标准模型理论的发展起到了十分重要的推动作用.
e+e-→W+W-反应可以精确确定W±玻色子的质量,许多物理学家在理论上从不同侧面对e+e-→W+W-反应做过研究. Lemoine M等人[1-5]曾讨论过e+e-→W+W-过程电弱修正和软光子修正;Beenakker W等人[6-8]针对特定的极化态计算了硬光子韧致辐射修正;Hagiwara K等人[9-10]基于最小超对称模型讨论了e+e-→W+W-过程;Aeppli A等人[11]初步讨论了e+e-→W+W-→4fermions过程,实验上,LEP实验组也对此过程做过观测.
在e+e-碰撞中,W玻色子主要是通过e+e-→W+W-过程产生的. 当质心能量在W+W-阈值处附近时,总截面对mW非常敏感,因而可以通过阈值扫描测量mW. 当质心能量在W+W-阈值以上时,W玻色子的质量可以通过测量其衰变产物的动量来确定. 大型正负电子对撞机(the large electron-positron collider,LEPC)曾采用阈值扫描和直接测量对W玻色子进行了测量. 其中,阈值扫描法具有较大的统计不确定性(~200 MeV);由于直接测量的数据统计有限,W玻色子质量不确定度约为33 MeV[12]. 结合LEPC,Tevatron和ATLAS的测量结果,目前W玻色子的质量为mW=(80.379±0.012) GeV[13]. 随着北京正负电子对撞机(Beijing Electron-Positron Collider,BEPC)于2022年左右关闭,为了在国际高能物理领域占有一席之地,我国科学家提出建设下一代环形正负电子对撞机(the circular electron positron collider,CEPC). 在CEPC上可以对W玻色子的质量和衰变宽度等物理量进行更加精确的测量,在CEPC上采用阈值扫描可获得2.5 MeV的测量精度,采用直接测量可获得3 MeV的测量精度,且测量可以直接在CEPC对撞能量区(
$\sqrt s $ ~240 GeV)进行.现有研究工作大多从有限高阶圈图角度研究e+e-→W+W-过程反应截面,并未涉及无穷高阶修正. 相对于已有的研究工作,本研究将从另一角度——即考虑混合链图传播子修正下e+e-→W+W-反应截面的解析计算. 在SM理论框架下讨论e+e-→W+W-反应,相应的传播子为光子γ,中间玻色子Z和电子中微子νe. 此外,由于γ和Z参与多种不同物理过程的电弱相互作用,因而若要考虑由γ和Z以及它们之间的混合圈构成的混合链图传播子,其构架问题将十分复杂. 本研究首先分析了SM中γ-Z混合链图传播子的构架方式,通过对各圈图传播子重新归类和组合,得到了相应的链图传播子的解析表达式,再通过在壳重整化方案中引入抵消项,从而获得重整化链混合链图传播子的严格解析结果. 同样本研究还给出了电子中微子链图传播子的严格解析结果. 进而,本研究将此结果应用到粒子反应e+e-→W+W-中,获得了在重整化链图传播子传递电弱作用时e+e-→W+W-的反应截面. 最后,结合CEPC实验,讨论了在W+W-产生能量阈值附近W玻色子质量不确定度对反应截面的影响,并讨论了在CEPC对撞能区可产生的W+W-事例数.
HTML
-
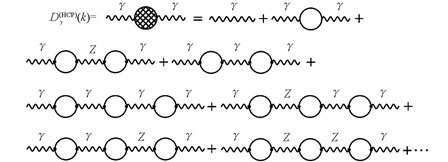
在SM中,γ和Z参与各种不同物理过程的相互作用,因而其混合链图传播子的构架方式十分复杂. 对于γ,其混合链图传播子Dγ(HCP)(k)的构架方式见图 1.
从图 1可以看出,γ混合链图传播子可以展开成树图、一圈图、两圈图……以至无穷圈图,且每个圈图又参与多种不同物理过程的相互作用. 将图 1中的所有图形重新排列,可以将它们重新归类. 将只含有γ参与相互作用的所有圈图归为第1类:
对于“单纯”的γ链图传播子,根据Dyson链图传播子理论[14],可将其表示为
将含有“2个”γ-Z混合圈图(其中:γ-Z圈和Z-γ且对等出现)的所有图形归为第2类:
各圈图之和可以表示为:
其中,
同样,对于“单纯”的Z链图传播子,可将其表示为
以此类推,便可以表示出含有“4个”γ-Z混合圈图,含有“6个”γ-Z混合圈图……的图形表示出来. 最后作者可将γ混合链图传播子表示成图 2.
从图 2可以看出,Dγ(HCP)(k)为一个“无穷级数”
其中:
完成(3)式的级数求和(暂时不考虑该级数的收敛条件),可将Dγ(HCP)(k)表示成
类似于对Dγ(HCP)(k)的分析处理,也可获得Z,γ-Z混合链图传播子的构架方式. 相应的混合链图传播子的解析表达式为
(5)-(7)式中各自能圈图均为发散量. 通过在壳重整化方案引入相应的抵消项
便可得到重整化混合链图传播子,只需将(5)-(7)中的
$\sum\nolimits_{\rm{T}}^{{\rm{ab}}} {({\rm{k}})} $ 替换成$\mathop \Sigma \limits^ \wedge {\kern 1pt} _{\rm{T}}^{{\rm{ab}}}({\rm{k}})({\rm{a}}, {\rm{b}} = \gamma , {\rm{Z}}) $ . 由于$\mathop \Sigma \limits^ \wedge {\kern 1pt} _{\rm{T}}^{{\rm{ab}}}({\rm{k}}) $ 的数量级为~10-2,因而满足级数收敛条件. 对(5)-(7)式中的各自能圈图,文献[15-16]均作过十分详细的讨论. 限于篇幅,本研究不再给出各自能圈函数的具体表达式.在SM中,电子中微子参与3种不同物理过程的相互作用. 相对于其树图阶传播子Sν(p)=ip/p2,类似于对γ,Z链图传播子的处理,可将中微子重整化混合链图传播子表示成
其中:
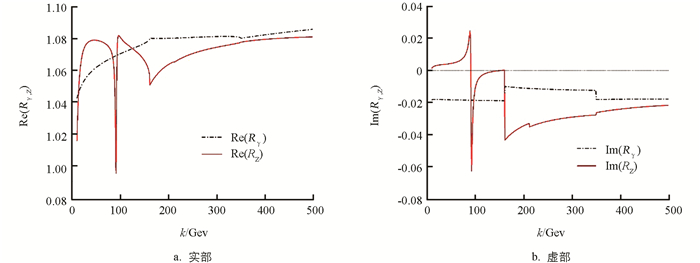
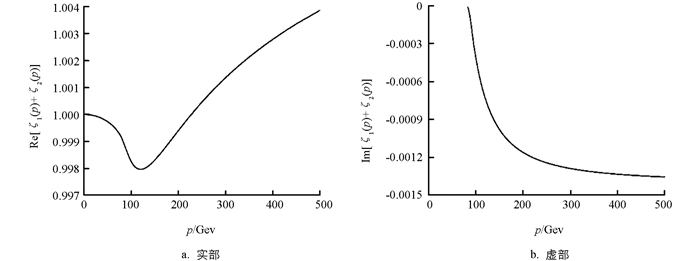
${\zeta _1}(p) = \frac{{2 - \mathop \Sigma \limits^ \wedge {\kern 1pt} _L^\nu (p)}}{{2 - 2\mathop \Sigma \limits^ \wedge {\kern 1pt} _L^\nu (p)}}, {\zeta _2}(p) = \frac{{\mathop \Sigma \limits^ \wedge {\kern 1pt} _L^\nu (p)}}{{2 - 2\mathop \Sigma \limits^ \wedge {\kern 1pt} _L^\nu (p)}} $ . ζ1(p)和ζ2(p)可理解为链图传播子对树图传播子的相对修正.利用在壳重整化方案,中微子重整化自能圈图为至此,本研究获得了γ-Z混合链图传播子和νe链图传播子的解析结果. 本研究关于混合链图传播子的讨论也可为探讨现代量子场论中一般复杂传播子的理论研究与应用提供某些学术参考价值. 为了具体讨论链图传播子对相应的树图传播子的相对修正,图 3给出了重整化γ混合链图传播子Dγ,R(HCP)(k)对γ树图传播子的相对修正Rγ(k)=Dγ,R(HCP)(k)/Dγ(k)和Z混合链图传播子对Z树图传播子的相对修正RZ(k)=DZ,R(HCP)(k)/DZ(k)随传播子能量的变化. 可以看出,γ,Z混合链图传播子对其树图的相对修正符合电弱修正量级. 由于中微子与W,Z玻色子耦合时,耦合顶点会出现γμ(1-γ5)项,若考虑中微子链图传播子修正,则耦合顶点中的γμ(1-γ5)项将变成[ζ1(p)+ζ2(p)]γμ(1-γ5)项,可将[ζ1(p)+ζ2(p)]理解为相对修正因子. 图 4给出了[ζ1(p)+ζ2(p)]的实部和虚部随p的变化. 从图 4可以看出,在较大能量范围内,链图传播子修正对其树图传播子的相对修正十分微小.
-
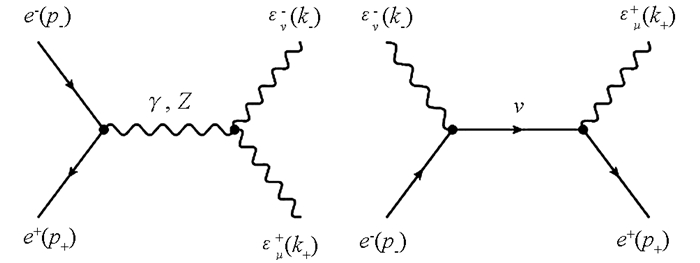
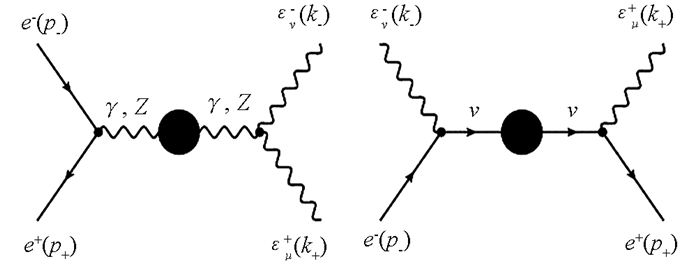
将所获得混合链图传播子应用到e+e-→W+W-反应中. 树图阶e+e-→W+W-反应过程的Feynman图见图 5. 若考虑混合链图传播子修正,相应的Feynman图见图 6.
在质心系中,Mandelstam变量定义为
式中,p±表示入射正负电子的动量,k±表示出射W±的动量. 在忽略电子质量情况下,最低阶微分截面可以表示成[17]
其中,不变矩阵元M0为
相应的混合链图传播子修正下的微分截面可表示为
其中,不变矩阵元MC为
完成|M0|2和|MC|2的计算,可得到相应的非极化微分截面. 完成(15)和(18)式中关于dΩ的积分
$\sigma=2 \pi \int_{0}^{\pi} \frac{\mathrm{d} \sigma}{\mathrm{d} \varOmega} \sin \theta \mathrm{d} \theta $ ,便得到相应的总截面. 微分截面和总截面的解析计算式十分复杂,限于篇幅,本文不再给出具体表达式.
-
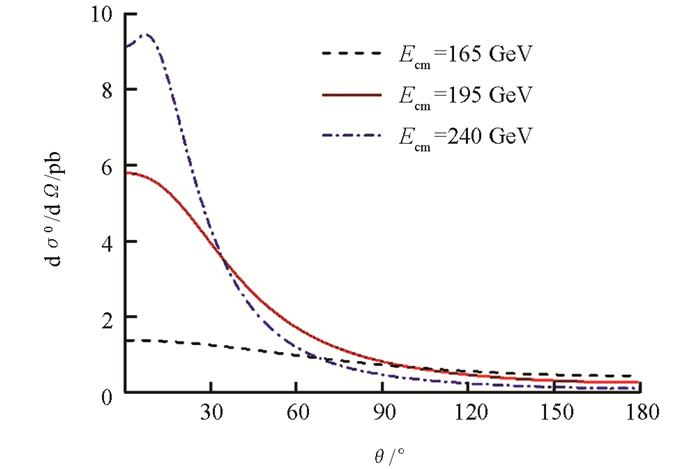
在计算具体数值时,各物理量的值取自粒子物理数据[13]:mW=80.379 GeV,mZ=91.187 6 GeV,α=1/137.0359 99,mH=125.09 GeV,mt=173.21 GeV,me=0.510 999 MeV,mμ=105.658 4 MeV,mτ=1.776 86 GeV,sW2=0.231 12. 图 7给出了质心能量分别为165 GeV,195 GeV和240 GeV时树图阶微分截面随散射角的变化. 从图 7中可以看出,随着质心能量的增加,微分截面随散射角的增加衰减越来越快.
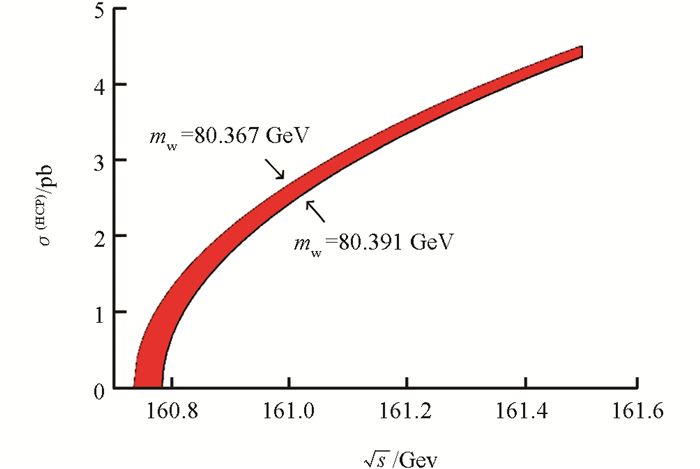
目前,综合LEP,Tevatron和ATLAS的实验数据,W玻色子的质量不确定度为12 MeV. 在W+W-阈值附近,W玻色子质量不确定度对总截面的影响很大. 图 8给出了W玻色子质量不确定mW=80.379-0.12+0.12 GeV度对总截面的影响. 在质心能量为161 GeV处,混合链图传播子修正下的总截面σ(HCP)=2.561 9-0.130 0+0.123 7pb. 在CEPC上,可通过阈值扫描测量e+e-→W+W-总截面,从而精确测量W玻色子的质量.
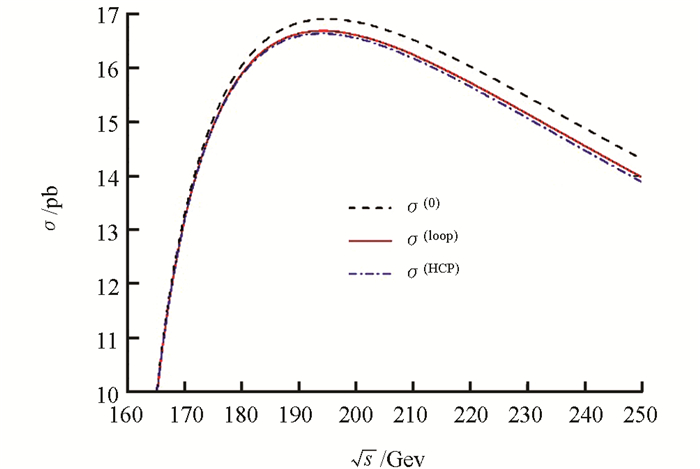
从(15)和(18)式可以看出,当质心能量达到产生W玻色子对阈值时,随着质心能量的增加,总截面会相应增加;由于总截面与质心能量平方成反比,因而当总截面达到峰值后又随着质心能量的增加而减小. 图 9给出了树图阶、传播子圈图修正和混合链图传播子修正下的总截面随质心能量的变化. 从图 9中可以看出:①在2mW到250 GeV质心能量范围内,混合链图传播子修正下的总截面σ(HCP)对树图阶总截面σ0约有1%到2%的压低效应,而σ(HCP)与圈图修正下的总截面σ(loop)结果很接近;②在质心能量为195 GeV时,总截面最大,之后总截面随质心能量的增加缓慢减小;③在对撞能量为240 GeV处,总截面与峰值相比减小12.75%,因而CEPC无需将对撞能量调到195 GeV,可直接在240 GeV对撞能区对W玻色子进行精确测量.
CEPC将作为Z-工厂(质心能量~91.2 GeV)运行2年;在W+W-阈值附近(158~172 GeV)运行1年,设计对撞亮度为10×1034cm-2s-2;作为Higgs工厂(240 GeV)运行7年,设计对撞亮度为3×1034cm-2s-2 [18]. 表 1给出了在不同质心能量下的总截面. 在W+W-能量阈值附近,若取161 GeV作为参考,总截面约为2.6 pb,则在CEPC上W+W-产生阈值附近运行一年可产生~8×107个事例数;而在240 GeV对撞能区可产生~108个事例数. 这可为精确测量W玻色子的质量提供数据保障.
-
本研究首先在标准模型理论框架下讨论了γ,Z,νe混合链图传播子的构架方式,并获得了相应的重整化混合链图传播子的严格解析结果. 进而,采用“混合链图传播子修正下的反应截面”这种计算模式,讨论了混合链图传播子修正下的e+e-→W+W-反应截面,获得了相应的解析结果和数值结果. 最后,结合CEPC对撞亮度和运行时间,讨论了CEPC在W+W-阈值附近和240 GeV两个对撞能区可产生W+W-的事例数.







 DownLoad:
DownLoad: