Empirical Research on Collaborative Development of Producer Service Industry and Modern Manufacturing in Chongqing Liangjiang New Area Based on L-V Model

生产性服务业与现代制造业之间是只有单方面的影响即此消彼长，还是存在着协同互动的双向关系?针对此问题，本文借助L-V模型关于不同种群之间竞争/共生等关系分析两产业部门流动的关联要素及维持系统平衡、实现产业之间协同发展的契合点.

20世纪40年代，美国生态学家Lotka(1925)和意大利数学家Volterra(1926)提出的种间竞争方程(简称L-V模型)对现代生态学理论的发展有着重大影响，奠定了种间竞争关系的理论基础，其核心要义是共同存在于一个生态系统中的种群，受各种群的影响，种群间的演变规律可以依据L-V模型来描述.生产性服务业和现代制造业组成的系统与生态系统类似，具有其一般属性特征，因此可以应用该模型研究2个产业之间的协同发展关系.

该模型是对研究单个事物或单方面影响的logistic模型的延伸，对研究不同物种之间的双向协同作用具有更大的优势^[16-17].根据L-V模型，种群之间协同作用关系的微分方程组为：

式中：M，N为t时刻M，N物种种群数量，对应生产性服务业、现代制造业的产业规模；α_m，α_n：M，N为种群增长率，对应两产业发展现状对产业未来发展的作用；β_m，β_n为M，N物种(两产业)自身发展的制约性参数；γ_mn，γ_nm为N物种对M物种的竞争系数、M物种对N物种的竞争系数，表明2个物种(产业)共生一个系统会产生相互影响，且有多种作用关系(表 1)，其绝对值越大表示物种(产业)之间作用越多、要素交流互动越容易.

依据公式(1)、(2)模型的参数取值不同，对生产性服务业和现代制造业共存于一个系统的共生作用关系进行分析与预测，不同的共生作用关系模型参数关系有如下情形^[14-15].

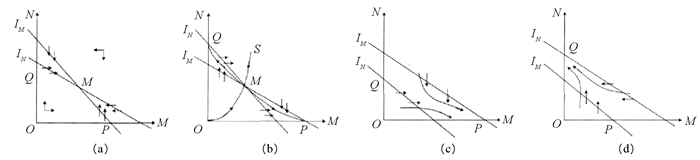
设β_m，β_n＞0，γ_mn，γ_nm＞0，模型的平衡位置一般有4个：①原点O(0，0)；②直线M=0与直线L_N：α_n-β_nN-γ_nmM的交点$\left( {0, \frac{{{\alpha _n}}}{{{\beta _{nm}}}}} \right)$；③直线N=0与直线L_M：α_m-β_mM-γ_mnN的交点$P\left( {\frac{{{\alpha _m}}}{{{\beta _m}}}, 0} \right)$；④2直线l_M和l_N的交点M(M^*，N^*).由于2直线l_M和l_N的斜率小于0，2直线的位置关系存在图2所示的4种可能：

1) 在图 1-a中，直线l_M与l_N相交于第一象限的正平衡点M，在直线l_M上因$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = 0$，l_M是该模型的垂直倾线，它把第一象限一分为二，在l_M上方$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = 0$＜0，在l_M下方$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = 0$＞0；在直线l_N上$\frac{{{\rm{d}}N}}{{{\rm{d}}t}} = 0$=0，l_N是该模型的水平倾线，在l_N上方$\frac{{{\rm{d}}N}}{{{\rm{d}}t}} = 0$＜0，在l_N下方$\frac{{{\rm{d}}N}}{{{\rm{d}}t}} = 0$＞0；在第一象限内，无论从何点出发，最终都将趋于平衡点M.这表明，不管生产性服务业和现代制造业现状处于何种程度，在竞争共生关联作用下，其结果都将达到稳定的平衡状态.此时，两产业应当倾向于专业化方向发展，并集聚已有优势打造新产业，促进自身的持续发展.

2) 在图 1-b中，直线l_M与l_N也相交于第一象限的平衡点M，但M点是模型的鞍点，图示有4条分界线：在OM和SM左面任意点，当t趋于无穷大时，两产业将趋于平衡点Q，其竞争结果是生产性服务业衰败而现代制造业持续发展，规模为Q；在OM和SM右面任意点，当t趋于无穷大时，两产业将趋于平衡点P，竞争结果是现代制造业发展趋于衰败而生产性服务业持续发展，规模为P.这种作用下表明生产服务业从制造业分离专业化发展并没有促进生产要素的有效配置而是阻碍了制造业的发展.

3) 在图 1-c中，经检验，直线l_M与l_N在第一象限不相交，没有正平衡点，当t趋于无穷大时，在第一象限的任意点其运动轨迹终将趋于点P，表明其竞争共生作用的结果是现代制造业因动力不足走向衰败而生产性服务业将继续发展.

4) 在图 1-d中，经检验，直线l_M与l_N在第一象限不相交，没有正平衡点，当t趋于无穷大时，在第一象限的任意点其运动轨迹终将趋于点Q，表明其竞争共生作用的结果是生产性服务业走向衰败而现代制造业将继续发展.在(c)，(d)情况下均应推进产业的延伸，方能持续发展.

借鉴竞争共生作用关系对两产业发展的分析，设β_m，β_n＞0，γ_mn，γ_nm＜0，模型的平衡位置有4个：①原点O(0，0)；②直线L_N与M轴的点Q$\left( {\frac{{{\alpha _n}}}{{{\beta _n}}}, 0} \right)$，0；③直线L_M与N轴的交点P$\left( {0, \frac{{{\alpha _m}}}{{{\beta _m}}}} \right)$；④2直线的交点M(M^*，N^*).由于2直线斜率大于0，此时，两产业之间的资金、技术等生产要素表现为双向流通，产业之间发展互为支撑.

在上述模型的4个平衡位置点中，①，②，③3个点均会导致两产业或其一发展趋于衰败而不稳定，仅有点M(M^*，N^*)即$\left( {\frac{{{\alpha _m}{\beta _n} - {\alpha _n}{\gamma _{mn}}}}{{{\beta _m}{\beta _n} - {\gamma _{mn}}{\gamma _{nm}}}}, \frac{{{\alpha _n}{\beta _m} - {\alpha _m}{\gamma _{nm}}}}{{{\beta _m}{\beta _n} - {\gamma _{nm}}{\gamma _{mn}}}}} \right)$，属于稳定状态，表明两产业在同一区域环境下相互提供支撑、互利共生从而实现两产业之间的协同发展，是我们应当着重关注和分析的发展状态^[16-17].

基于L-V模型及在生产性服务业和现代制造业之间相互作用的应用分析，讨论了竞争共生和互利共生情境下两产业之间的互动作用和产业发展趋势与发展策略，下面以两江新区为例予以实证分析.

重庆两江新区紧邻长江和嘉陵江，规划总面积1 200 km²，可开发550 km². 2016年，两江新区实现GDP 2 261亿元；规模以上工业总产值4 892亿元，固定资产投资2 043亿元，实际利用外资32.1亿美元.两江新区工业开发区于2010年7月18日挂牌，规划用地238 km²，可开发面积212 km²，是两江新区重点打造的万亿级先进制造业基地，包括龙兴、水土和鱼复工业园，规划面积分别为111 km²、60 km²、67 km².其中龙兴工业园重点产业含高端装备制造、汽车生产等；水土高新技术产业园区有生物医药研制、软件研发等；鱼复工业园区有轨道交通、现代物流产业等.两江新区工业开发区共规划建设313 hm²生产性服务业用地，布局在龙兴片区、鱼复片区和水土片区.

两江新区水土片区道路交通设施较完善，该区域距水土高速公路收费站3.5 km，距水土镇约4 km，目前周边均为制造业企业，商业繁华度较差；龙兴片区区域道路交通设施较完善，临两江大道，距龙兴高速公路收费站0.5 km，距复盛镇约3 km，区域周边均为制造业企业，商业繁华度较差.两江新区鱼复片区区域道路交通设施较完善，距龙兴高速公路收费站1 km，距复盛镇约3 km，周边均为制造业企业，商业繁华度较差.

总体上，研究区生产性服务业楼宇竣工率低，未按期开竣工项目比较高；现阶段制造业增速显著，但总量有限，制造业服务外置水平较低，城市基础设施不尽完善，造成企业和从业人员入驻意愿下降，导致发展动力需求不足，因此，生产性服务业具有较大的发展空间.

本研究范围为两江新区生产性服务业及制造业，以两江新区工业开发区为主体，尤其是水土、龙兴和鱼复工业园.研究数据主要来自两江新区2010-2017年统计年鉴、两江新区城市规划和土地利用总体规划；部分数据通过研究区实地调研和问卷调查、测量及网络辅助收集.另外广泛查阅并收集了国内外关于生产性服务业与现代制造业发展的研究成果等.

利用L-V模型研究生态系统中不同种群相互作用时，要求所得数据是连续的，但实际中很多研究对象的数据非连续而呈离散化形式，因此，本研究对生产性服务业和现代制造业之间协同互动作用的探讨，拟将该模型予以形式转化，以适应离散化数据的实情.

离散化前后，公式(1)，(2)与公式(3)，(4)中的相关参数对应关系如下：

要使表达式成立，则须δ_m＞0，δ_n＞0，且δ_m≠1，δ_n≠1，因此，γ_mn，γ_nm同ω_m，ω_n在取值上正负一致.

本研究中，关于生产性服务业部门划分依据国家统计局及相关规范，主要统计交通运输、金融业、房地产业、信息服务产业；现代制造业依据国家制造业分类规范和研究区实际予以界定，主要统计汽车、电子信息、轨道交通、高端装备、航空产业、节能环保、新能源新光源、生物医药等产业.数据包括2010年两江新区成立到2017年，采用统计年鉴上的数据并结合其他经济统计数据(表 2).根据L-V模型，先测算模型转化后表达式中的参数值，在根据函数关系测算L-V模型中参数具体值.

本研究采用非线性最小二乘法，利用Eviews9.0软件对模型中相关参数值予以概略估测，结果见表 3.

经对各参数估计值做显著性检验，在5%的显著性水平下通过t检验，ω_m，ω_n在10%的显著性水平下通过t检验.表明δ，κ，ω的估测值在10%显著水平下均有效，微分方程的R²都大于0.9，因而模型拟合性较好.由表 4离散模型参数的对应关系，得到表 4中L-V模型中的参数值.

1) 增长系数α_m，α_n值为正，表明研究区两产业只依靠自身也能得以发展、扩大规模，但现代制造业对自身发展的促进作用较生产性服务业大.目前两江新区现代制造业总体规模尚不大，生产性服务业发展与区域发展水平还不协调，因此，加快配套设施建设，增强区域对产业的吸引力，快速推进两江新区现代制造业的发展是生产性服务业的发展与繁荣不可或缺的必备要件.

2) 阻碍性参数β_m，β_n值为正，表明两产业规模扩大过程中存在边际效益递减状况，且生产性服务业更明显.可能原因一是因为该产业受地方产业政策限制而进入门槛高，市场化水平较低而使其发展活力不够；二是因为该区域传统产业仍占主导地位，技术创新不够，高端技术依赖国外引进，现代制造业产业升级进程较缓，阻碍了生产性服务业的转型升级和发展.因此，改革两江新区的产业发展政策，合理设置准入门槛，加强技术创新提升先进技术的研发和应用能力，促进现代制造业升级，有助于生产性服务业的提档升级.

3) 互动作用参数γ_mn，γ_nm值为负，表明产业之间为互利共生关系，产业发展互为支撑和依赖，一个产业的发展提升会带动另一个产业的发展，最终双方都得到发展.协同互动发展机制表现为：一是生产性服务业能够提供现代制造业发展所需的人才、技术、资金、制度等的支持和保障推动其生产率提高；二是现代制造业发展到一定阶段可以为生产性服务业部门的办公设施提供保障，随着规模的进一步扩大，也会增加对资本、人力资源、信息等要素的需求，从而促进生产性服务业部门的发展和升级；三是γ_mn较γ_nm小，表明产业之间的带动作用上，现代制造业对生产性服务业的拉动作用更大，说明两江新区传统产业若要向现代制造业转型则需要解决生产性服务业发展动力不足的困境，从而在互利共生作用方式下，两产业都得到有效的发展.

4) 当环境波动时，存在有的均衡点不稳定的情况.根据前述分析，生产性服务业与先进制造业会的4个均衡点中，仅有第四个点M(M^*，N^*)属于稳定状态，该均衡点坐标表达式：$\left( {\frac{{{\alpha _m}{\beta _n} - {\alpha _n}{\beta _{mn}}}}{{{\beta _m}{\beta _n} - {\gamma _{mn}}{\gamma _{nm}}}}, \frac{{{\alpha _n}{\beta _m} - {\alpha _m}{\beta _{nm}}}}{{{\beta _m}{\beta _n} - {\gamma _{nm}}{\gamma _{mn}}}}} \right)$.采用Jacobian矩阵方法计算，该坐标点的特征值为M(-1.298，-0.216)，相应的均衡值M(1 527.38，746.42)，此时趋于稳定.结果表明，两江新区生产性服务业增加值在1 527.38亿元、现代制造业增加值在746.42亿元时达到稳定状态.现阶段还低于这个水平，因此，研究区两产业都会持续发展直至达到稳定，当发展到一定阶段高于这个均衡值的时候就会逐渐减速降低到平衡状态.

本研究引入生物学中的生态共生理论研究成果L-V模型并以两江新区为例证探求2个产业之间的协同发展作用机制.研究表明，生产性服务业和现代制造业之间在构成的区域产业系统内表现为在适当竞争的情况下保持良好的协同发展关系；两产业之间通过资金、技术、人才、组织、制度等要素的互动流通实现互利共生，互为支撑从而实现共同发展，在互利共生作用过程中实现2个产业的转型升级与进步；最后采用Jacobian矩阵测算出两江新区两产业发展均衡稳定点的特征值，分析了两产业发展最后的稳定状态.本研究将推进学界对生产性服务业与制造业互动发展关系的认识，并可以作为区域产业发展政策制定的借鉴和参考，因此，本研究具有较好的理论和实践意义.

本研究表明，两产业在协同发展过程中互动作用程度不一样，生产性服务业对制造业的促进相对较小，而制造业对生产性服务业的促进相对更大.因此，以L-V模型分析结果为依据，以供给侧改革思想为指引，对于研究区两产业的发展提出如下建议：

一是加快两江新区基础设施建设及土地供应，推进现代制造业发展，从而拉动生产性服务业的发展.如积极调整区域城市规划，增加餐饮、娱乐、住房(尤其是公租房)、交通、教育、医疗、零售业等配套用地并助力建设，满足入驻企业和员工的衣、食、住、行、教育、医疗等需求，增强两江新区生产性服务业和现代制造业发展的吸引力，为生产性服务业的发展提供动力和源泉.

二是优化区域市场结构，降低两产业相关企业准入门槛，从注重事前准入转为注重事中事后监管.实施负面清单管理模式，推进实施工商登记“先照后证”制和注册资本认缴登记制.对外商投资实行准入前国民待遇加负面清单的管理模式，减少和取消对外商投资准入限制，让更多的企业和资金入驻两江新区，增强产业发展的动力.

三是制定两江新区产业发展的优惠政策，健全有利于生产性服务业发展的投融资体系.引导和鼓励金融机构对符合国家产业政策和两江新区要求的生产性服务业企业给予信贷支持，支持中小企业通过资本市场进行融资.将针对生产性服务业经营企业的优惠政策如土地供应数量与价格等覆盖面扩展到全部生产性服务业行业.探索分行业管理制度，即不同行业优惠力度有所不同.条件成熟时可以探索一企一策，即根据具体企业经营表现和绩效评价结果，动态调整税费优惠政策.

四是畅通两产业之间资源的流通渠道.两江新区管委会应配套对应措施，加快两产业之间的资源流通，促使生产性服务业的资金、技术、人才、信息等快速流向制造业，充分发挥资源的重要作用，促进企业间的合作交流及社会化服务与制造环节的有效连接.