On Sum-Balaban Index of Graphs Based on Contraction of Cycles

Bo DENG; Xue-li SU; Xiao-min REN

doi:10.13718/j.cnki.xsxb.2019.04.002

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

The Balaban index (also called \lt i \gt J \lt /i \gt index) of a connected graph \lt i \gt G \lt /i \gt is denoted as $ J\left( G \right) = \frac{m}{{m - n + 2}}\sum\limits_{uv \in E\left( G \right)} {\frac{1}{{\sqrt {{\sigma _G}\left( u \right){\sigma _G}\left( v \right)} }}} $ and the Sum-Balaban index of a connected graph \lt i \gt G \lt /i \gt is denoted as $ SJ\left( G \right) = \frac{m}{{m - n + 2}}\sum\limits_{uv \in E\left( G \right)} {\frac{1}{{\sqrt {{\sigma _G}\left( u \right) + {\sigma _G}\left( v \right)} }}} $ where \lt i \gt m \lt /i \gt , \lt i \gt n \lt /i \gt are the edge number and vertex number of \lt i \gt G \lt /i \gt , respectively, and \lt i \gt σ \lt /i \gt \lt sub \gt \lt i \gt G \lt /i \gt \lt /sub \gt ( \lt i \gt u \lt /i \gt ) (resp. \lt i \gt σ \lt /i \gt \lt sub \gt \lt i \gt G \lt /i \gt \lt /sub \gt ( \lt i \gt v \lt /i \gt )) denotes the total distance from \lt i \gt u \lt /i \gt to all the other vertices of \lt i \gt G \lt /i \gt . The Balaban index and the Sum-Balaban index have been widely used in various QSAR and QSPR studies. In this paper, we have proved that the Balaban index and the Sum-Balaban index increase by the contraction of cycles. Then we see the varieties of this operation and propose a new method for these two indices.

Other Articles By Authors

On Sum-Balaban Index of Graphs Based on Contraction of Cycles

Received Date: 26/05/2018

Available Online: 20/04/2019

Key words:

Abstract: The Balaban index (also called \lt i \gt J \lt /i \gt index) of a connected graph \lt i \gt G \lt /i \gt is denoted as $ J\left( G \right) = \frac{m}{{m - n + 2}}\sum\limits_{uv \in E\left( G \right)} {\frac{1}{{\sqrt {{\sigma _G}\left( u \right){\sigma _G}\left( v \right)} }}} $ and the Sum-Balaban index of a connected graph \lt i \gt G \lt /i \gt is denoted as $ SJ\left( G \right) = \frac{m}{{m - n + 2}}\sum\limits_{uv \in E\left( G \right)} {\frac{1}{{\sqrt {{\sigma _G}\left( u \right) + {\sigma _G}\left( v \right)} }}} $ where \lt i \gt m \lt /i \gt , \lt i \gt n \lt /i \gt are the edge number and vertex number of \lt i \gt G \lt /i \gt , respectively, and \lt i \gt σ \lt /i \gt \lt sub \gt \lt i \gt G \lt /i \gt \lt /sub \gt ( \lt i \gt u \lt /i \gt ) (resp. \lt i \gt σ \lt /i \gt \lt sub \gt \lt i \gt G \lt /i \gt \lt /sub \gt ( \lt i \gt v \lt /i \gt )) denotes the total distance from \lt i \gt u \lt /i \gt to all the other vertices of \lt i \gt G \lt /i \gt . The Balaban index and the Sum-Balaban index have been widely used in various QSAR and QSPR studies. In this paper, we have proved that the Balaban index and the Sum-Balaban index increase by the contraction of cycles. Then we see the varieties of this operation and propose a new method for these two indices.

HTML

对简单图G，分别用m(G)和n(G)表示G的边集和顶点集，其边数和点数分别记为m = m(G)和n = n(G). N_G(v)表示顶点v在G中的邻集.在图G中，顶点u和v的距离记为d_G(u，v)，顶点u到其它各顶点的距离之和记为σ_G(u)，即$\sigma_{G}(u) = \sum\limits_{\omega \in V(G)} d_{G}(u, \omega)$.文献[1]介绍了一种关于连通图的新的拓扑指标，称为Balaban指标，或简称为J指标：

类似地，Sum-Balaban指标^[2]为

Balaban指标和Sum-Balaban指标都是非常有用的且具有良好性质的分子描述器，被广泛应用于QSAR和QSPR的各方面的研究^[1-2].更多关于Balaban指标、Sum-Balaban指标和其它化学指标的研究，参考文献[3-11].

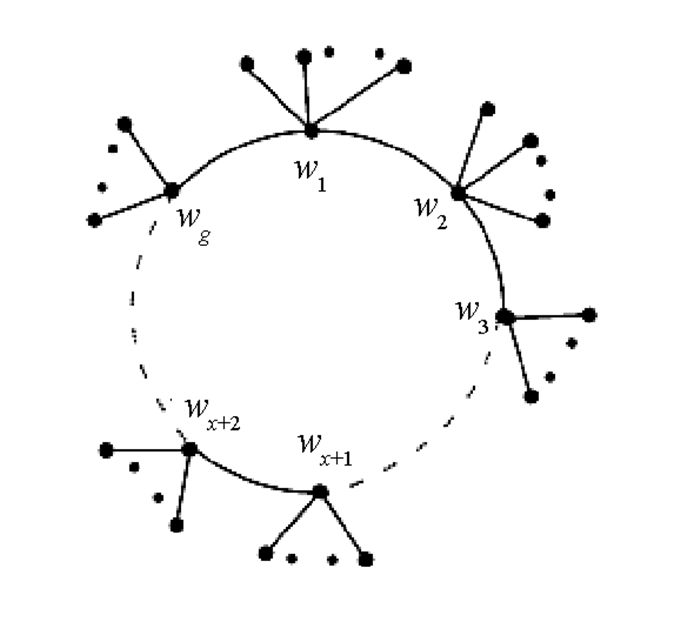
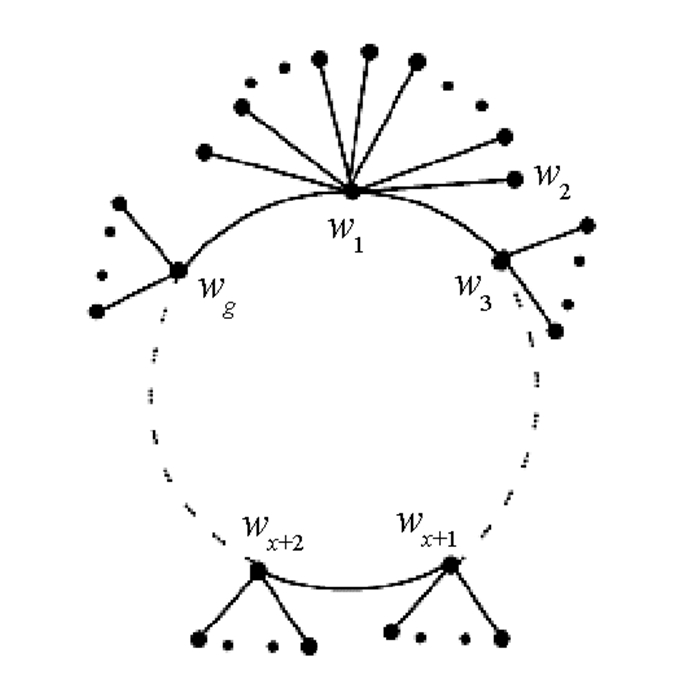
设U₀ = U_n(S_w₁，S_w₂，…，S_{w_g}) (见图 1)是一个围长为g的单圈图，其中S_{w_i}是以圈上的点w_i为中心的星图，对1≤i≠j≤g，满足|n(S_{w_i})-n(S_{w_j})|≤1.图U₁(见图 2)是由U₀经过收缩边w₁w₂，并把w₁w₂变成悬挂边得到的，即

定理1 SJ(U₀) < SJ(U₁).

证从图U₀到图U₁可以看到，除了顶点w₂外，其它顶点的距离之和都变小了.即对u∈V(U₀)(或u∈V(U₁))，有σ_U₀(u)＞σ_U₁(u)，以及σ_U₀(w₂) < σ_U₁(w₂).因此，对任意边uv∈E(U₀)(E(U₁))，u，v≠w₂，有：

对于顶点w₁，w₂，由于圈的收缩，容易看到在U₀中w₂与其它顶点的距离之和大于在U₁中w₁与其它顶点的距离之和，即σ_U₀(w₂)＞σ_U₁(w₁).因此，对于w₂u∈E(U₀)，u∈D_U₀(w₂)和w₁u∈E(U₁)，有u∈D_U₁(w₁)∩D_U₀(w₂)，其中D_U₁(w₁)∩D_U₀(w₂) = D_U₀(w₂)，则：

由图U₀可以看到，连接顶点w₂的边有w₁w₂，w₂w₃和悬挂边.接下来需要证明如下不等式：

因为σ_U₁(w₁) < σ_U₀(w₂)和σ_U₁(w₃) < σ_U₀(w₃)，则

如果σ_U₀(w₁)+σ_U₀(w₂)≥σ_U₁(w₁)+σ_U₁(w₂)，则由(5)式，不等式(4)成立.否则，

当U₀的围长是偶数时，可以看出，对顶点w₂，其增加的部分σ_U₁(w₂)－σ_U₀(w₂)等于顶点w₁的减少部分σ_U₀(w₁)－σ_U₁(w₁)，故

因此，只需讨论U₀的围长是奇数的情况.可以看到：

从图U₀到图U₁，我们有：

由Δ(U₀) = d_U₀(w₃)≥d_U₀(w₂)和(7)，(8)式，故σ_U₁(w₃) < σ_U₀(w₂).因此，由σ_U₁(w₁) < σ_U₀(w₁)，可得

不失一般性，设

则存在非负整数k₁，满足σ_U₀(w₂)+σ_U₀(w₃) = σ+k₁.类似地，由(6)式和(9)式，存在正整数k₂和k₃，分别满足σ_U₁(w₁)+σ_U₁(w₂) = σ+k₂和σ_U₁(w₁)+σ_U₁(w₃) = σ－k₃.如果k₁≥k₂，则

因此由(9)式，不等式(4)成立.否则

在U₀的围长是奇数的条件下，讨论k₂和k₃的关系.令：

从U₀到U₁，可以看出：

因此

由Δ(U₀) = d_U₀(w₃) < Δ₁^-，以及(10)式和(11)式，则有k₁ < k₂ < k₃.于是

因为对x＞0，$\frac{1}{\sqrt{x}}-\frac{1}{\sqrt{x+s}}$是单调递减函数，其中s是正整数，k₂ < s < k₃+k₁，则对σ－k₃ < σ，我们有

当s增加时，不等式的左边会变大；当s减少时，不等式的左边会变小.因此

故有：

因此，不等式(4)成立.由(2)，(3)，(4)式和Sum-Balaban指标的定义，定理1成立.

容易看出定理1对J(G)也成立.本文所提出的新的比较方法是基于圈收缩变换的.对于任意一个单圈图，经过圈收缩后，对于原图中的大部分顶点的距离之和都会变小，但存在唯一一个顶点w₂的距离之和是变大的.考虑把图的边集划分为若干部分进行比较.特别地，对含有顶点w₂的边，需要进行恰当的组合，再进行有效的比较.定理1采用的方法也可以推广到双圈图以及k(k≥3)圈图，有助于对这类化学指标进行值极刻画.

Figure (2) Reference (11)

Name
	Name cannot be empty!
E-mail
	Mailbox cannot be empty! Mailbox cannot be empty!
Telephone
	Mobile number cannot be empty! Please enter a valid mobile number!
Title

Content
Verification Code

[1]	BALABAN AT.Topological Indices Based on Topological Distances in Molecular Graphs[J].Pure & ApplChem, 1983, 55(2):199-206. Google Scholar
[2]	DENG H Y.On the Sum-Balaban Index[J].MATCH Commun Math Comput Chem, 2011, 66(2):273-284. Google Scholar
[3]	DONG H W, GUO X F.Character of Graphs with Extremal Balaban Index[J].MATCH Commun Math Comput Chem, 2010, 63(3):799-812. Google Scholar
[4]	ZHOU B, TRINAJSTIC N.Bounds on the Balaban Index[J].CroatChemActa, 2008, 81(2):319-323. Google Scholar
[5]	SUN L L.Bounds on the Balaban Index of Trees[J].MATCH CommunMathComput Chem, 2010, 63(3):813-818. Google Scholar
[6]	DENG H Y.On the Balaban Index of Trees[J].MATCH Commun Math Comput Chem, 2011, 66(1):253-260. Google Scholar
[7]	GAO W, BABY S, SHAFIQ MK, et al.On Randic Indices of Single-Walled TiO2 Nanotubes[J]. UPB Scientific Bulletin(Series B), 2017, 79(1):93-100. Google Scholar
[8]	GAO W, JAMIL MK, JAVED A, et al.Sharp Bounds of the Hyper Zagreb Index on Acyclic, Unicylic and Bicyclic Graphs[J/OL]. Discrete Dynamics in Nature and Society, 2017, 2017: 1-5[2018-4-20]. https://doi.org/10.1155/2017/6079450. Google Scholar
[9]	钟琴, 牟谷芳.矩阵Hadamard积谱半径的新上界[J].西南师范大学学报(自然科学版), 2018, 43(12):1-5. Google Scholar
[10]	贾弯弯, 王正攀.Rees矩阵定理的简明刻画[J].西南大学学报(自然科学版), 2017, 39(12):86-89. Google Scholar
[11]	钟琴, 周鑫.非负不可约矩阵Perron根的上界[J].西南大学学报(自然科学版), 2017, 39(10):75-78. Google Scholar

Message Board

On Sum-Balaban Index of Graphs Based on Contraction of Cycles

Abstract

References

Access History

通讯作者: 陈斌, bchen63@163.com

Article Metrics

Access History

Other Articles By Authors