-
热量的传递过程是通过热传导、热对流和热辐射3种方式进行的,其中,热传导是通过固体或者静止流体传播热量;热对流局限于液体和气体,并且往往涉及流体固体边界的热交换;热辐射能量是通过电磁波传递的[1]. 在计算物体温度场时,固态物体内部热量的传递方式为热传导,将热对流和热辐射作为边界条件. 分析传热问题时,从不同的角度出发可将传热问题分为3类:①根据热量传递的维度可将热传导问题分为一维热传导问题、二维热传导问题和三维热传导问题;②根据是否考虑温度场随时间变化,可分为瞬态温度场和稳态温度场;③根据是否考虑材料性能随温度的变化,可分为变系数热传导问题和常系数热传导问题.
热量传递引起的温度场变化涉及到生物[2]、医疗[3]、材料[4-6],建筑结构[7-9]等多个领域,在温度场研究中,将与温度分布相关的物理参数称为热工参数,包括比热、热传导系数以及密度,其中密度随温度变化微小. 对于特殊材料或环境温度变化范围较小的情况,如自然环境等,可不考虑材料热工参数随温度的变化. 然而,大多材料的热工参数都会随着温度的变化而改变,以钢材为例,各国规范均给出了钢材热工参数随温度的变化规律[10]. 为了求解热工参数随温度变化的热传导问题,国内外学者做了大量研究. 在稳态温度场的研究中,Ünal[11]基于平面板模型提出一种考虑热传导率随温度线性变化的一维稳态热传导问题求解方法;Hussein[12]通过理论推导,在球坐标系中求解了实心球体在有内部热源、考虑材料热传导率随温度线性变化的情况下的一维稳态传热问题,并且对比了使用3种不同材料时的温度分布情况;高仲仪[13]采用λ变换法求解变系数稳态热传导问题,该方法假设热传导率随温度线性变化且热传导率与温度一一对应,将温度逆向表示为热传导率的函数,通过求解热传导率进而得到温度场;严治军[14]给出了具有对流换热边界条件的一维常系数热传导差分解法,考虑多层不同材料时温度场分布,最后采用FORTRAN语言编制成热传导解析的计算程序. 瞬态温度场的研究也大多是基于一定假设简化得到的计算结果,魏光坪[15]、康为江[16]和彭友松[17]在研究自然条件下的桥梁温度场时,由于自然环境下温度变化较小,通常将材料热工参数视为常数,考虑了3种热传递方式对结构温度场的影响;李国强等[18]在对火灾下二维钢板-混凝土组合楼板温度场分析时,考虑结构的热对流和热辐射边界条件,并探究火灾位置和分布对楼板温度场的影响,通过对结果进行参数分析,提出了适用于火灾下的楼板温度计算的简化公式;胡克旭等[19]采用有限单元法,假定单元温度随着位置坐标线性变化,计算了火灾下压型钢板-混凝土组合楼板在存在热对流和热辐射,同时考虑建筑材料热工参数随温度变化时的温度场.
实际上,由于材料比热和热传导率均会随着温度变化,加之边界条件的复杂性,使得求解偏微分方程得出解析解是极少数情况. 采用数值方法计算,能有效简化计算过程. 常见的数值解法有有限元法、有限体积法、边界元法和有限差分法等,这些方法中,有限差分法具有简单且稳定的优点[20]. 本研究基于热传导的有限差分方程,使用MATLAB编程计算结构温度场. 以简化的一维变系数瞬态温度场分布模型为例,阐明考虑材料热工参数随温度变化时的有限差分法计算过程,并建立有限元模型进行结果验证.
全文HTML
-
理论推导求解物体温度场一般采用解析法和数值法. 其中,解析法是以热传导方程为基础,求解偏微分方程,寻求物体温度分布与时间和位置关系的函数表达式,即T(x,y,z,t). 实际能采用解析法求解的热传导问题是极少数情况,因此,通常采用有限差分的数值方法建立传热的有限差分方程,求解温度场近似值[21],通过减小单元格大小(时间步长、空间步长)来提高计算精度.
有限差分方程的建立可通过两种方式完成:一是基于热传导方程建立差分方程,二是基于能量平衡建立差分方程.
-
热传导方程为:
式中:λ(T)为热传导率;ρ为材料密度;C(T)为比热容. (1)式表达了温度在空间上的分布与温度随时间变化的关系:
基于热传导方程建立传热的差分方程,就是以热传导方程为基础,用差分代替微分,将偏导写成差分形式进行求解. 对于任意连续函数,使用泰勒级数将x0相邻两点函数值f(x-1)和f(x1)在x0处展开得:
(2) 式+(3)式得到f(x)在x0处沿着x方向二阶导数,略去高阶项,得到:
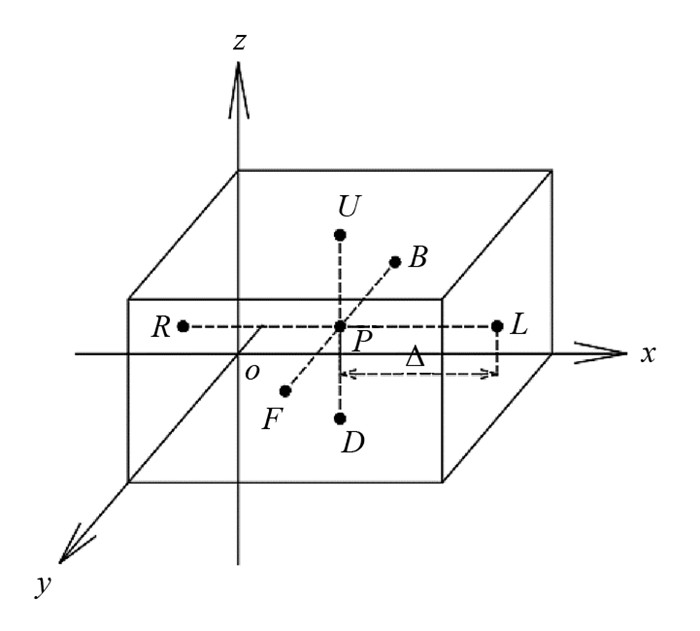
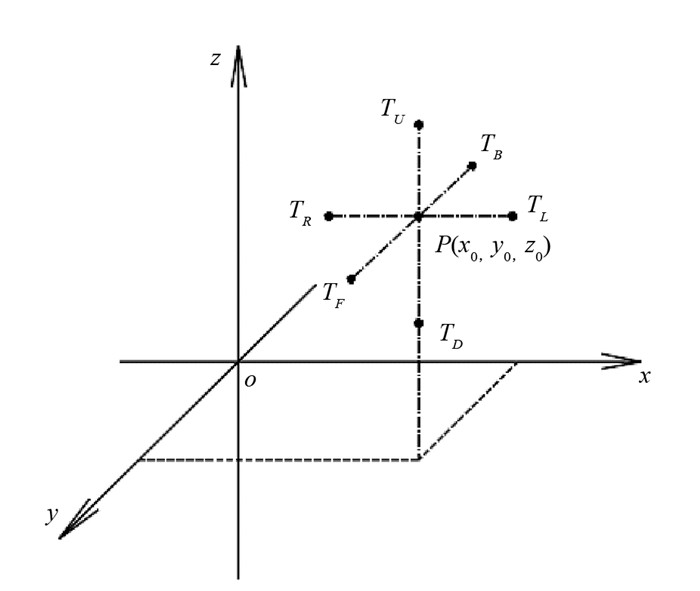
同理,在图 1所示三维直角坐标系中,与点
$ P\left(x_0, y_0, z_0\right)$ 相邻的上下左右前后6个点的温度值分别为$T_U, T_D, T_L, T_R, T_F, T_B $ .则
$ T(x, y, z)$ 在点$ P\left(x_0, y_0, z_0\right)$ 处各方向二阶偏导可表示为:取空间间隔
$\Delta x=\Delta y=\Delta z=\Delta $ ,时间间隔为Δt,时间偏导采用向前差分格式则有:式中:T′为P点下一时刻温度值. 将(5)式和(6)式带入(1)式中,得到基于热传导方程的差分方程,整理得:
式中:
$ F O=\frac{\alpha \Delta t}{\Delta^2}=\frac{\lambda}{\rho c} \frac{\Delta t}{\Delta^2}$ ,为傅里叶数. 此时,(7)式左侧取不同时刻温度可得到方程的不同差分形式:若左端温度均取此时刻温度T(t0),则为显式格式;左端温度均取下一时刻温度T(t0+Δt),则为隐式格式;若采用加权平均的形式,可表示为: -
基于能量平衡建立差分方程,是根据单元能量平衡的思想进行的,即:单元内输入热量和输出热量的差值,引起单元温度变化. 差值为正,单元温度升高;差值为负,单元温度降低.
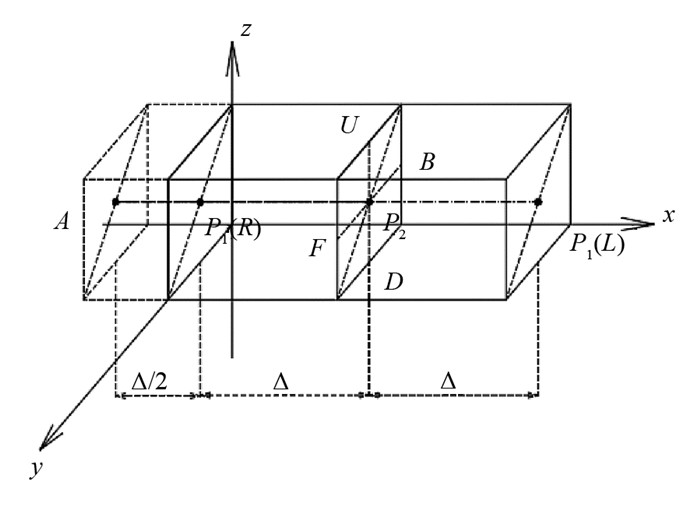
图 2中A为外界节点(边界条件),P1为边界节点,P2为中间节点. 图 3中,与点P相邻的6个点U,D,L,R,F,B分别代表点P上下左右前后相邻点. 为简化计算,令网格间隔Δx=Δy=Δz=Δ,因此相邻各点到P的距离均为Δ. 节点i到相邻节点j之间的传热系数为Kij,基于傅里叶定律,从节点j到i的热量为[13]:
单元内蓄积的能量使得单元内部温度发生变化,节点i的能量平衡方程为:
式中:
$ V_i=\Delta x \Delta y \Delta z=\Delta^3$ ,为相邻坐标点之间的单元体积(在边界时$V_i=\frac{\Delta^3}{2} $ );$K_{i j}=\frac{\lambda_{i j} A_{i j}}{L_{i j}} $ ,为节点i与节点j之间的传热系数,在边界时Kij=hjAij,hj为周围温度为Tj时表面Aij上的表面传热系数,λij为节点i与节点j之间的热传导率;Aij为垂直于节点i与节点j之间传热方向的平均表面积;Lij为节点i与节点j之间的距离,因此,在无内部热源时,节点i的热平衡方程为:图 3中,中间节点
图 2中,边界节点(假设为左侧边界,右侧同理)
令
$A=\Delta^2, L_{P R}=\Delta, V_P=\frac{\Delta^3}{2} $ 带入(12)式,得:对(12)式右侧进行向前差分,左侧采用加权平均的形式,整理得:
式中,若β=0,方程为显式格式;β=1,方程为隐式格式. 得到差分方程,结合相应的边界条件即可得到温度场分布.
-
实际情况中多为三维热传导问题. 但在处理一些特定问题时,适当做出假设,可将三维简化为二维或一维情况.
按照1.2节思路,可得二维热传导差分方程为:
一维热传导差分方程为:
同于1.1节,若β=0,方程为显式格式;β=1,方程为隐式格式.
-
对于显式格式的有限差分方程,在计算时,涉及到方程的稳定性问题.
令式(14)中β=0,得显式格式差分方程:
由(17)式可知,由于FO>0,所以当T的系数(1/FO-6) < 0时,T越大T′就会越小,即此时刻温度越大下一时刻的温度越小,显然违背热力学原理. 因此,(1/FO-6)≥0同理. 对于二维和一维有相同的约束.
内部节点:
边界节点(对流边界条件):
式中:Bi=hΔ/λ,时间步长限制取(18)式与(19)式所得交集. 在一维直角坐标系中,由(19)式可得时间步长限制为:
1.1. 基于热传导方程的差分方程
1.2. 基于能量平衡的差分方程
1.3. 差分方程的特殊形式
1.4. 显示差分的稳定性要求
-
以“一维无热源具有热对流边界条件的热传导问题”为例,分别介绍是否考虑材料热工参数随温度变化两种情况时的温度场求解方法.
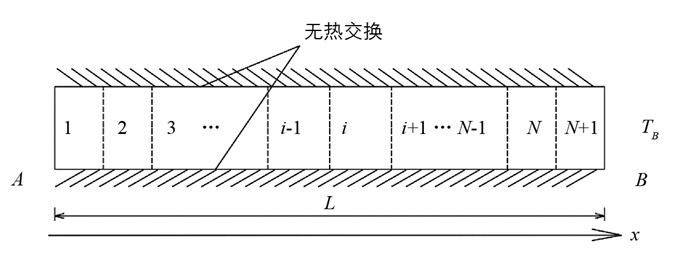
已知初始时刻所有节点温度均为T(X,0)=T0;左边界环境温度满足TA=A(t),右边界环境温度满足TB=B(t),表面传热系数为hw. 将构件沿x方向均匀划分为N个单元格(图 4).
-
在上述一维热传导问题中,取
$T(X, 0)=T_0=20^{\circ} \mathrm{C} $ 左侧环境温度取国际标准升温曲线(ISO834)[14]温度值$A(t)=20+345 lg (8 t+1), B(t)=20{ }^{\circ} \mathrm{C}, L=4 \mathrm{~m}, N=80 $ . 热工参数见表 1.对于常系数热传导问题,采用显式和隐式格式均可求解. 由(13)式和(16)式得节点i的差分方程,其中显式差分格式为:
隐式差分格式为:
-
采用显式格式求解热传导问题时,首先根据精度要求,选取空间网格Δ大小,再根据显式格式的稳定性要求确定时间步长Δt,最后依据递推关系(21)式,结合边界和初始条件计算得到温度场.
由1.4节可知,显式格式需要对方程的稳定性作出要求. 取
$\Delta=\frac{L}{N}=0.05 \mathrm{~m} $ ,根据(18)式和(20)式得:计算时间取100 min,则所需时间步为:
取Δt=49.062 5 s时,FO=0.187 5,Bi=5/3,带入(21)式,得:
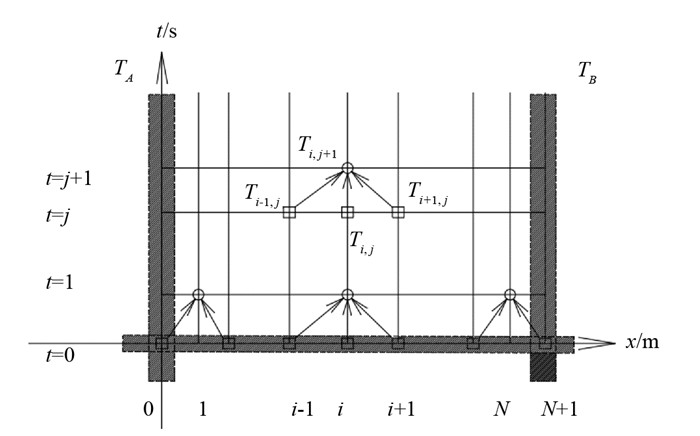
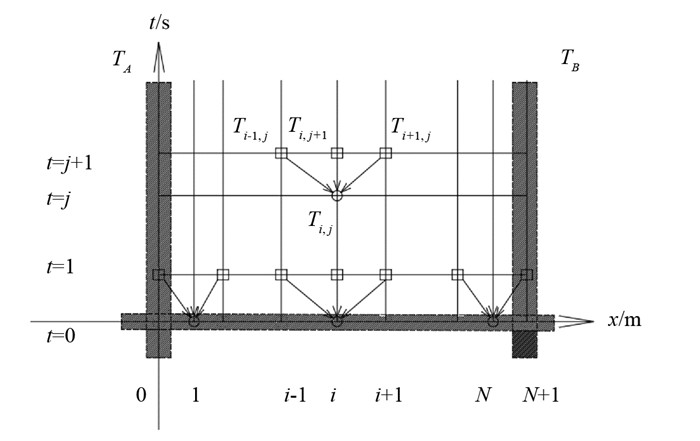
至此得到该例的显式差分格式,已知初始温度分布T(x,0)和边界条件TA,TB,依次沿着时间步向下计算,可得到所有节点任意时刻温度值. 计算示意图见图 5,横轴为节点位置,i表示第i个节点;纵轴为时间步,j表示第j个时间步.
由图 5可见,显示格式递推关系清晰,易于计算,根据(23)式采用MATLAB编程计算温度场即可.
-
采用隐式格式求解热传导问题时,根据精度要求,选取空间网格Δ大小,隐式格式的差分方程没有稳定性要求,时间间隔可根据需求选定. 通过(22)式,结合边界和初始条件,求解方程组,得到温度场.
初始时刻,时间步j=0. 由(22)式得每个节点上的差分方程为:
式中:Tij表示i节点j时刻的温度值,TAj和TBj分别表示左右两侧j时刻环境温度值.
写成矩阵形式:
其中:
$ K 1=1 /(2 F O)+(1+B i) \cdot 2 F O ; K=2 F O \cdot B i$ .同理,对于下一个时间步,也可以得到相似的矩阵形式. 由此可见:对于隐式格式,虽然方程的计算不受时间间隔的影响,但是在求解每一时刻各节点温度值时,都需要联立方程组,这使得求解计算量变大. 隐式格式求解结构图见图 6.
此时基于矩阵(24)求解,所采用的方法称为三对角矩阵算法(TDMA). 取时间间隔为20 s,空间间隔为0.05 m,采用MATLAB编程求解矩阵,即可得到温度场.
-
实际上,当温度较高时,材料热工参数会随着温度的改变而改变,即热传导系数和比热为温度的函数. 在计算考虑材料热工参数随着温度的温度场时,本研究采用欧洲规范EC3[2]中钢材热传导系数和比热容随温度变化关系,由于材料热工参数为温度的函数,热传导方程变为非线性方程,基于热传导方程直接求解会十分复杂. 采用能量平衡的方法建立显式格式的差分方程,计算时遵循以下流程:在已知初始温度场T0时,依据EC3规范计算得到初始时刻的热工参数λ0和C0,再通过λ0和C0依据差分方程计算新的温度场T1. 即已知前一时刻热工参数,可得到下一时刻新的温度场,多次计算得任意时刻的温度场Tn. 依据以上思路和1.2节内容,建立差分方程.
对于中间节点,有:
一维状态下
$\Delta x=\Delta ; A=1 ; V_P=A \times \Delta x=\Delta $ ,其中λ12是在温度$T=\frac{T_1+T_2}{2} $ 时根据EC3规范计算的值. (25)式右侧取向前差分,得到显式差分格式:对于左侧边界节点,有:
取显式格式:
同理,右侧边界节点:
若仍取Δ=0.05 m. 由于采用显式差分格式,需满足(20)式与(22)式的稳定性要求. 结合(25)式和(26)式可知,取初始的热工参数λ0和C0满足要求,带入参数得:
可以看出,方程中温度的系数都是随温度变化的,即非线性方程,采用2.1节中直接求解的方法无法得到结果. 根据(28)式-(29)式,考虑温度引起的材料性能改变(遵循EC3规范公式),使用MATLAB编程即可计算得到温度场.
2.1. 常系数热传导方程
2.1.1. 常系数显式求解
2.1.2. 常系数隐式求解
2.2. 变系数热传导方程
-
基于以上内容,使用ABAQUS分别建立不考虑热工参数随温度变化的有限元模型MODEL0与考虑热工参数随温度变化的有限元模型MODEL1,相关参数与2.1节、2.2节保持一致. 模型MODEL0与模型MODEL1均采用C3D8T单元,分别取x=0 m和x=1 m处截面温度进行对比.
-
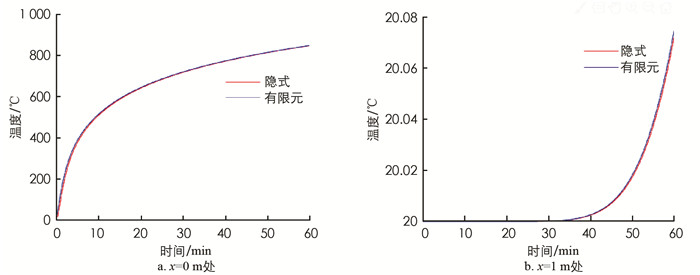
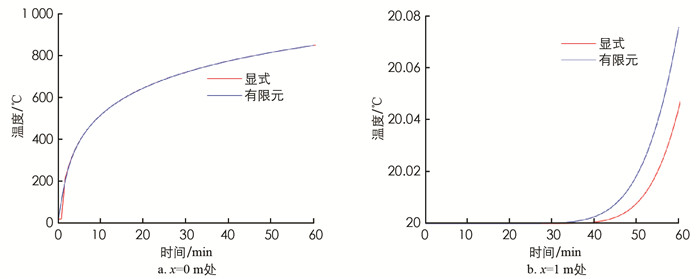
不考虑材料性能随温度变化时,可采用显式和隐式两种差分格式计算,将2.1节计算结果与MODEL0计算结果进行对比,以验证计算结果的准确性(图 7和图 8).
由图 7可知,当不考虑材料热工参数随温度变化时,采用隐式差分计算结果与ABAQUS有限元模拟结果高度吻合. 在环境温度采用国际标准升温曲线(ISO834)时,在边界处,物体内部温度变化与环境温度变化形式相同,均呈对数形式;在远离边界的物体内部,温度变化幅度随着离边界距离的增大而减小,且温度变化呈指数形式. 对比图 8可知,采用显式差分计算在x=0 m边界处与ABAQUS有限元模拟结果几乎重合;在距离边界1 m处,显式计算结果和ABAQUS模拟结果随着时间的增加相差变大,但总体差距仍然较小(小于0.03 ℃). 产生这一现象的原因在于,隐式差分计算中采用的TDMA方法计算结果是理论上的精确解,而显式差分的精度取决于网格划分的大小.
-
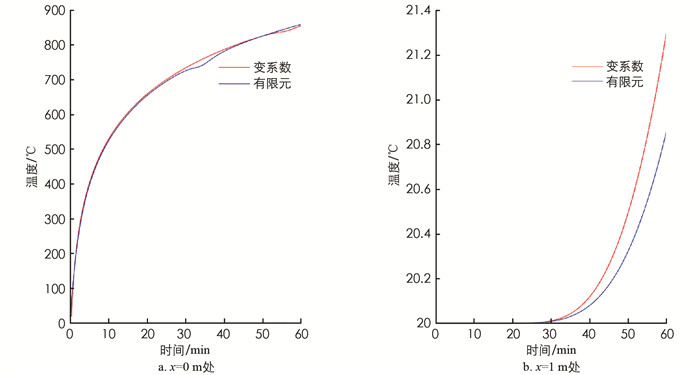
当考虑材料性能随温度变化时,采用显式差分格式计算,将2.2节计算结果与MODEL1进行对比,以验证计算结果的准确性(图 9)所示.
由图 9可见,当考虑材料热工参数随温度变化时,使用2.2节中方法计算结果与ABAQUS有限元模拟结果吻合度较高. 在环境温度采用国际标准升温曲线,考虑材料热工参数随温度变化时,在边界处物体内部温度变化与环境温度变化形式相同,呈对数形式;远离边界的物体内部,温度变化范围随着离边界距离的增大而减小,温度变化呈指数形式. 温度场变化规律与常系数相同. 可以看到,采用有限差分法计算时,不论是常系数还是变系数计算结果与相应的有限元模拟结果均存在误差,这些误差主要来源于两方面:①采用有限元软件计算的温度场实际上是采用有限单元法计算的,本研究采用的是有限差分法,不论是有限单元法还是有限差分法,两者作为数值方法本身就与精确解存在误差;②两种方法的计算精度不仅与时间网格、空间网格大小的有关,有限单元法中选取的形函数、有限差分法中省略的高阶项也直接影响相应的计算精度.
-
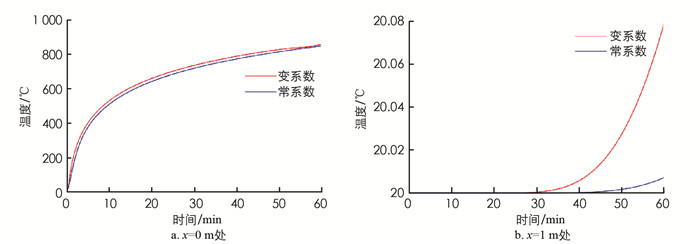
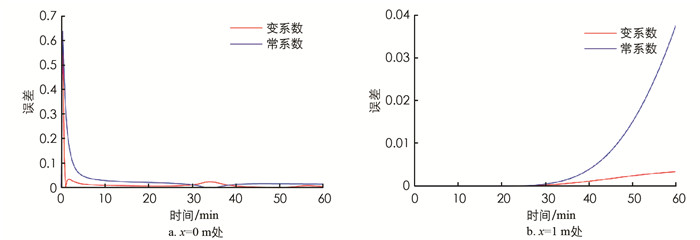
为探究是否考虑材料热工参数对温度场的影响,分别取离左侧边界x=0 m,x=1 m处截面两种情况下显示格式计算所得温度场进行对比,并进行误差分析,结果见图 10和图 11.
由图 10可见,是否考虑材料热工参数随温度变化不影响温度分布规律,但改变了温度大小:考虑材料热工参数随温度变化时的温度相对于不考虑材料热工参数随温度变化时的温度偏高. 由图 11可见:采用有限差分法时不论是否考虑材料热工参数随温度变化,两者所产生的误差具有相同的变化规律,但不考虑材料热工参数随温度变化产生的误差总是高于考虑热工参数随温度变化的误差;图 11a中,除时间t=20 s时误差为60%,其余各个时间误差均小于10%,这是由于采用的升温曲线初始温度变化快,同时计算时所取时间步长较大引起的. 因此,当环境温度较高或温度变化速率较大时,计算物体温度场时应考虑材料热工参数随温度的变化,且取更小的时间空间网格以提高精度.
3.1. 常系数计算结果验证
3.2. 变系数计算结果验证
3.3. 常系数、变系数计算结果对比
-
本研究在推导求解变系数热传导问题的基础上,以具有热对流边界条件同时考虑材料热工参数随温度变化的一维瞬态热传导问题为例,采用有限差分法分析了当环境温度为国际标准升温曲线时物体内部温度分布情况,得到以下五点结论.
1) 基于能量平衡建立传热有限差分方程相对于从热传导方程出发建立传热有限差分方程,过程清晰、可考虑热工参数随温度变化的情况,更适用于特殊复杂情况.
2) 通过与相应的有限元模型计算结果对比表明:本研究采用基于能量平衡建立的有限差分解法能有效计算考虑材料热工参数随温度变化时的温度场.
3) 是否考虑材料热工参数随温度变化不影响温度分布规律,但影响温度大小:考虑材料热工参数随温度变化时得到的温度场,高于不考虑热工参数变化得到的温度场.
4) 在环境温度采用国际标准升温曲线(ISO834)时,在边界处,物体内部温度变化与环境温度变化形式相同,均呈对数形式;在远离边界的物体内部,温度变化幅度随着离边界的距离增大而减小,且温度变化呈指数形式.
5) 依据本研究的思路也可计算二维、三维温度场,进一步就特定的环境温度提出相应的物体内部温度场简化计算方法.



 下载:
下载: