一个n阶矩阵A=(a_ij)(i，j∈{1，2，…，n})的第二immanant定义为

其中χ是S_n关于划分(2，1，…，1)的不可约特征标. 特别地，χ(σ)=ε(σ)[F(σ)-1]，其中ε是交替特征标，F是固定点的个数.

第二immanant是积和式与行列式之间的一个不变量. 文献[1]指出计算第二immanant的时间复杂度是n⁴. 假设矩阵A的阶为n(≥2)，因为d₂(A)的项对应于det A的因子(F(σ)-1)(σ∈S_n). 因此有

其中A(i)是删除矩阵A的第i行和第i列得到的子矩阵. 例如，假设

根据公式(1)，可得d₂(A)=18.

令G是含有n个顶点的图. A(G)是图G的(0，1)-邻接矩阵. d_i表示顶点v_i的度. 矩阵

称为图G的拉普拉斯矩阵，其中D(G)是对角元素为{d₁，d₂，…，d_n}的n阶度矩阵.

多项式

称作图G的第二immanantal多项式，记作d₂-多项式，其中I是n×n单位矩阵. 为了强调图G，系数通常记作c_k(G)(0≤k≤n).

两个图是共第二immanant的，是指这两个图分享相同的第二immanantal多项式. 图H与图G是共第二immanant的，但不是同构的，则称H是G的一个共第二immanant伙伴. 如果图G没有共第二immanant伙伴，则称图G是由第二immanantal多项式确定的.

图谱理论中的一个经典问题：什么样的图是由多项式确定的?在图多项式理论中，这是一个困难的问题. 近几年，这个问题受到了许多学者的关注. 一些图G已经被证明是由矩阵(xI-L(G))的行列式确定的，例如双星状图^[2]、沙漏图^[3]、Z_n图^[4]、T-形树^[5]、∞-图^[6]等.

最近，学者们考虑了什么样的图是由矩阵(xI-L(G))的积和式确定的. 文献[7]证明了完全图和圈是由矩阵(xI-L(G))的积和式确定的. 文献[8]证明了棒棒糖图是由(xI-L(G))的积和式确定的. 关于这个问题更多的研究，可参见文献[9-18].

文献[19]首次考虑了一个问题：什么样的图是由d₂-多项式确定的? 文献[19]证明了：几乎所有的树都有共第二immanant伙伴. 特别地，文献[1]证明了：如果图G和H是两个正则图，则G和H是共第二immanant的当且当

或

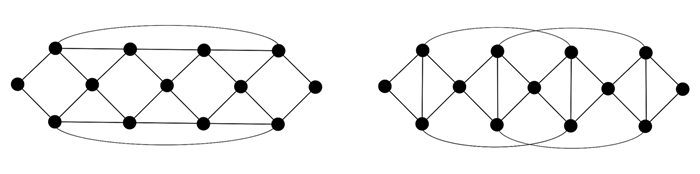
并且，文献[10]发现一对非正则的图对是共第二immanant的，如图 1所示.

基于文献[19]的探讨，存在一个有趣的问题：寻找一些图，既是由d₂-多项式确定的，也是由特征多项式det(xI-A(G))确定的. 本文围绕这个问题开展研究.

令$\mathscr{G}_n $是从完全图K_n删除至多5条边得到的图集. 文献[20]证明了$\mathscr{G}_n $中所有的图都是由其特征多项式确定的. 本文讨论$\mathscr{G}_n $中哪些图是由其第二immanantal多项式确定的. 意外的是，我们发现，无例外地，$\mathscr{G}_n $中所有的图都是由其第二imamnantal多项式确定的.

定理1  $\mathscr{G}_n $中所有的图都是由其第二immanantal多项式确定的.

本文剩余内容的结构如下：先给出一些d₂-多项式的性质；再给出定理1的证明；最后提出两个值得未来进一步研究的有意义的问题.

令图G=(V，E)表示一个含有非空点集V和非空边集E的无向简单图，即G是不含有环和重边的图.

图G=(V，E)的补图是G与G含有相同的点集和边集为{i，j}(i≠j当且仅当{i，j}∉E)的图. 对G的一个子图H，令G-E(H)表示从G中删除H中的边集得到的子图，G∪H表示不含有公共顶点的两个图G和H的并. 对任意的正整数l，令lG表示l个G的不交并. 为了方便起见，我们把含有n个顶点的完全图、路、圈和星分别记作K_n，P_n，C_n和K_1，n-1.

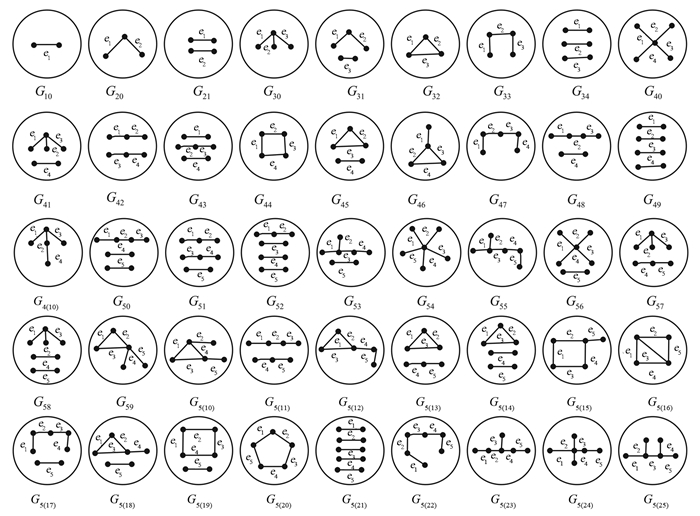
文献[21]指出，对n≥10，在$\mathscr{G}_n $中存在45个非同构图，并标记为G_ij(i=1，2，…，5；j=0，1，…，25)，如图 2所示.

引理1   ^[1]令G是含有n个顶点和m条边的连通图，(d₁，d₂，…，d_n)表示图G的度序列，L(G)是图G的拉普拉斯矩阵，且

则

其中τ(G)表示图G的生成树的个数.

由引理1，我们可以得到d₂-多项式的一些性质.

引理2  从图G的d₂-多项式的系数c₀(G)，c₁(G)和c_n(G)可以推断出G的顶点数、边数、生成树的个数.

引理3^[22]   如果G是G的补图，且G含有n个顶点，则

其中τ(G)是G的生成树的个数.

由引理3，我们计算出了$\mathscr{G}_n $中一些图的生成树的个数，如表 1所示.

由引理3，我们可得：

定理2  图G₁₀是由d₂-多项式确定的.

定理3  图G₂₀和G₂₁是由d₂-多项式确定的.

证   根据表 1，我们知道

由引理2可知，这意味着G₂₀和G₂₁是由d₂-多项式确定的.

定理4  图G₃₀，G₃₁，G₃₂，G₃₃和G₃₄是由d₂-多项式确定的.

证   根据G_3i(i=0，1，…，4)的图结构，我们知道

根据引理1，我们可以得到

这意味着G₃₂和G₃₃不是共第二immanant的.

同样地，解方程

我们得到这些方程的解n小于对应图的顶点数，矛盾. 所以，G₃₁和G₃₃，G₃₁和G₃₄，G₃₃和G₃₄分别都不是共第二immanant的.

由表 1，解方程

可以得出这些方程或者没有解，或者没有整数解.

由引理2及以上的讨论可知，图G₃₀，G₃₁，G₃₂，G₃₃和G₃₄是由d₂-多项式确定的.

定理5  图G₄₀，G₄₁，G₄₂，G₄₃，G₄₄，G₄₅，G₄₆，G₄₇，G₄₈，G₄₉和G₄₍₁₀₎是由d₂-多项式确定的.

证   根据图G_4j(j=0，1，…，10)的结构，我们可以得到|V(G₄₀)|≥5，|V(G₄₁)|≥6，|V(G₄₂)|≥6，|V(G₄₃)|≥7，|V(G₄₄)|≥4，|V(G₄₅)|≥5，|V(G₄₆)|≥4，|V(G₄₇)|≥5，|V(G₄₈)|≥6，|V(G₄₉)|≥8和|V(G₄₍₁₀₎)|≥5.

由表 1得到，只有当n=4时，τ(G₄₄)-τ(G₄₆)=(n-4)n^n-5=0.如果n=4，由引理1，我们得到c₂(G₄₄)=16和c₂(G₄₆)=14. 这表明G₄₄和G₄₆不是共第二immanant的.

同样地，只有当n=-1，5时，有τ(G₄₄)-τ(G₄₇)=(-n²+4n-5)n^n-6=0.如果n=5，由引理1可知，在图G₄₄和G₄₇中，c₂(G₄₄)=212和c₂(G₄₇)=216. 这意味着G₄₄和G₄₇不是共第二immanant的.

类似地，只有当n=1，5时，τ(G₄₆)-τ(G₄₍₁₀₎)=(-n²+6n-5)n^n-6=0. 如果n=5，由引理1可得，c₂(G₄₆)=208和c₂(G₄₍₁₀₎)=212. 这说明G₄₆和G₄₍₁₀₎不是共第二immanant的.

根据表 1，解方程τ(G₄₀)-τ(G_4j)=0(j=1，2，3，5，6，10)，τ(G₄₁)-τ(G_4j)=0(j=2，3，4，5，6，8，9，10)，τ(G₄₂)-τ(G_4j)=0(j=3，5，6，7，8，10)，τ(G₄₃)-τ(G_4j)=0(j=4，5，6，8，9，10)，τ(G₄₄)-τ(G_4j)=0(j=5，8，9)，τ(G₄₅)-τ(G_4j)=0(j=8，9)，τ(G₄₇)-τ(G_4j)=0(j=8，10)，τ(G₄₈)-τ(G₄₉)=0.我们得到这些方程的根n小于对应图的顶点数，矛盾. 因此，图G₄₀和图G₄₁，G₄₂，G₄₃，G₄₅，G₄₆，G₄₍₁₀₎；图G₄₁和图G₄₂，G₄₃，G₄₄，G₄₅，G₄₆，G₄₈，G₄₉，G₄₍₁₀₎；图G₄₂和图G₄₃，G₄₅，G₄₆，G₄₇，G₄₈，G₄₍₁₀₎；图G₄₃和图G₄₄，G₄₅，G₄₆，G₄₉，G₄₍₁₀₎；图G₄₄和图G₄₅，G₄₈，G₄₉；图G₄₅和图G₄₈，G₄₉；图G₄₇和图G₄₈，G₄₍₁₀₎；图G₄₈和图G₄₉都分别不是共第二immanant的.

由表 1，解方程τ(G₄₀)-τ(G_4j)=0(j=4，7，8，9)，τ(G₄₁)-τ(G₄₇)=0，τ(G₄₂)-τ(G_4j)=0(j=4，9)，τ(G₄₃)-τ(G₄₇)=0，τ(G₄₄)-τ(G₄₍₁₀₎)=0，τ(G₄₅)-τ(G_4j)=0(j=6，7，10)，τ(G₄₆)-τ(G_4j)=0(j=7，8，9)，τ(G₄₇)-τ(G₄₉)=0，τ(G₄₈)-τ(G₄₍₁₀₎)=0和τ(G₄₉)-τ(G₄₍₁₀₎)=0. 我们可以得出这些方程或者没有解，或者没有整数根. 这说明G₄₀和G₄₄，G₄₇，G₄₈，G₄₉；G₄₁和G₄₇；G₄₂和G₄₄，G₄₉；G₄₃和G₄₇；G₄₄和G₄₍₁₀₎；G₄₅和G₄₆，G₄₇，G₄₍₁₀₎；G₄₆和G₄₇ G₄₈，G₄₉；G₄₇和G₄₉；G₄₈和G₄₍₁₀₎；G₄₉和G₄₍₁₀₎都分别不是共第二immanant的.

根据引理2和上述讨论可得，G₄₀，G₄₁，G₄₂，G₄₃，G₄₄，G₄₅，G₄₆，G₄₇，G₄₈，G₄₉和G₄₍₁₀₎是由d₂-多项式确定的.

定理6  图G₅₀，G₅₁，G₅₂，G₅₃，G₅₄，G₅₅，G₅₆，G₅₇，G₅₈，G₅₉，G₅₍₁₀₎，G₅₍₁₁₎，G₅₍₁₂₎，G₅₍₁₃₎，G₅₍₁₄₎，G₅₍₁₅₎，G₅₍₁₆₎，G₅₍₁₇₎，G₅₍₁₈₎，G₅₍₁₉₎，G₅₍₂₀₎，G₅₍₂₁₎，G₅₍₂₂₎，G₅₍₂₃₎，G₅₍₂₄₎和G₅₍₂₅₎是由d₂-多项式确定的.

证   根据图G_5j(j=0，1，…，25)的结构，我们可得|V(G₅₀)|≥8，|V(G₅₁)|≥8，|V(G₅₂)|≥9，|V(G₅₃)|≥7，|V(G₅₄)|≥6，|V(G₅₅)|≥6，|V(G₅₆)|≥7，|V(G₅₇)|≥7，|V(G₅₈)|≥8，|V(G₅₉)|≥5，|V(G₅₍₁₀₎)|≥5，|V(G₅₍₁₁₎)|≥7，|V(G₅₍₁₂₎)|≥5，|V(G₅₍₁₃₎)|≥6，|V(G₅₍₁₄₎)|≥7，|V(G₅₍₁₅₎)|≥5，|V(G₅₍₁₆₎)|≥4，|V(G₅₍₁₇₎)|≥7，|V(G₅₍₁₈₎)|≥6，|V(G₅₍₁₉₎)|≥6，|V(G₅₍₂₀₎)|≥5，|V(G₅₍₂₁₎)|≥10，|V(G₅₍₂₂₎)|≥6，|V(G₅₍₂₃₎)|≥6，|V(G₅₍₂₄₎)|≥6和|V(G₅₍₂₅₎)|≥6.

与定理5的证明类似，根据表 1可得：

只有当n=1，n=6时，τ(G₅₉)-τ(G₅₍₂₄₎)=n^n-7(-n³+8n²-13n+6)=0. 如果n=6，由引理1可得c₂(G₅₉)=780和c₂(G₅₍₂₄₎)=790. 这表明G₅₉和G₅₍₂₄₎不是共第二immanant的.

只有当n=1，n=5时，τ(G₅₍₁₀₎)-τ(G₅₍₁₅₎)=n^n-6(-n²+6n-5)=0. 类似地，如果n=5，根据引理1可得c₂(G₅₍₁₀₎)=106和c₂(G₅₍₁₅₎)=146. 这说明G₅₍₁₀₎和G₅₍₁₅₎不是共第二immanant的.

只有当n=3，n=5时，τ(G₅₍₁₀₎)-τ(G₅₍₁₆₎)=n^n-6(n²-8n+15)=0. 如果n=5，由引理1得到c₂(G₅₍₁₀₎)=106和c₂(G₅₍₁₆₎)=138. 这意味着G₅₍₁₀₎和G₅₍₁₆₎不是共第二immanant的.

只有当n=2，5时，τ(G₅₍₁₅₎)-τ(G₅₍₁₆₎)=n^n-6(2n²-14n+20)=0. 如果n=5，根据引理1可得c₂(G₅₍₁₅₎)=146和c₂(G₅₍₁₆₎)=138. 这说明G₅₍₁₅₎和G₅₍₁₆₎不是共第二immanant的.

只有当n=-1，5时，τ(G₅₍₁₅₎)-τ(G₅₍₂₀₎)=n^n-6(-n²+4n-5)=0. 如果n=5时，由引理1得到c₂(G₅₍₁₅₎)=146和c₂(G₅₍₂₀₎)=150. 这表明G₅₍₁₅₎和G₅₍₂₀₎不是共第二immanant的.

类似地，根据表 1，解方程τ(G₅₀)-τ(G_5j)=0(j=1，2，3，6，8，11，14，15，…，23)，τ(G₅₁)-τ(G_5j)=0(j=1，10，20)，τ(G₅₂)-τ(G_5j)=0(j=1，2，10，20)，τ(G₅₃)-τ(G_5j)=0(j=1，2，3，10，12，13，20)，τ(G₅₄)-τ(G_5j)=0(j=5，6，7，8，11，13，18，22，24，25)，τ(G₅₅)-τ(G_5j)=0(j=6，7，8，9，11，12，13，18，20，22，23，24，25)，τ(G₅₆)-τ(G_5j)=0(j=7，8，9，11，13，15，16，17，18，19，21，22，23，24，25)，τ(G₅₇)-τ(G_5j)=0(j=8，10，11，12，13，14，17，18，19，20，22，24，25)，τ(G₅₈)-τ(G_5j)=0(j=9，11，13，14，…，19，21，22，23，24，25)，τ(G₅₉)-τ(G_5j)=0(j=10，11，12，13，14，18，22，25)，τ(G₅₍₁₀₎)-τ(G_5j)=0(j=12，21，23)，τ(G₅₍₁₁₎)-τ(G_5j)=0(j=12，13，14，…，19，21，22，23，24，25)，τ(G₅₍₁₂₎)-τ(G_5j)=0(j=13，14，18，22，25)，τ(G₅₍₁₃₎)-τ(G_5j)=0(j=14，18，22，24，25)，τ(G₅₍₁₄₎)-τ(G_5j)=0(j=15，16，17，18，19，21，22，23，25)，τ(G₅₍₁₅₎)-τ(G_5j)=0(j=17，18，19，21，22，23)，τ(G₅₍₁₆₎)-τ(G_5j)=0(j=17，18，19，21，22，23)，τ(G₅₍₁₇₎)-τ(G_5j)=0(j=18，19，…，23)，τ(G₅₍₁₈₎)-τ(G_5j)=0(j=19，20，…，25)，τ(G₅₍₁₉₎)-τ(G_5j)=0(j=21，22，23)，τ(G₅₍₂₀₎)-τ(G₅₍₂₄₎)=0，τ(G₅₍₂₁₎)-τ(G_5j)=0(j=22，23)，τ(G₅₍₂₂₎)-τ(G_5j)=0(j=23，24，25})和τ(G₅₍₂₄₎)-τ(G₅₍₂₅₎)=0.我们得到这些方程的根n小于对应图的顶点数，矛盾. 因此，G₅₀和G_5j(j=1，2，3，6，8，11，14，15，…，23)，G₅₁和G_5j(j=1，10，20)，G₅₂和G_5j(j=1，2，10，20)，G₅₃和G_5j(j=1，2，3，10，12，13，20)，G₅₄和G_5j(j=5，6，7，8，11，13，18，22，24，25)，G₅₅和G_5j(j=6，7，8，9，11，12，13，18，20，22，23，24，25)，G₅₆和G_5j(j=7，8，9，11，13，15，16，17，18，19，21，22，23，24，25)，G₅₇和G_5j(j= 8，10，11，12，13，14，17，18，19，20，22，24，25)，G₅₈和G_5j(j=11，13，14，…，19，21，22，23，24，25)，G₅₉和G_5j(j=10，11，12，13，14，18，22，25)，G₅₍₁₀₎和G_5j(j=12，21，23)，G₅₍₁₁₎和G_5j(j=12，13，14，…，19，21，22，23，24，25)，G₅₍₁₂₎和G_5j(j=13，14，18，22，25)，G₅₍₁₃₎和G_5j(j=14，18，22，24，25)，G₅₍₁₄₎和G_5j(j=15，16，17，18，19，21，22，23，25)，G₅₍₁₅₎和G_5j(j=17，18，19，21，22，23)，G₅₍₁₆₎和G_5j(j=17，18，19，21，22，23)，G₅₍₁₇₎和G_5j(j=18，19，…，23)，G₅₍₁₈₎和G_5j(j=19，20，…，25)，G₅₍₁₉₎和G_5j(j=21，22，23)，G₅₍₂₀₎和G₅₍₂₄₎，G₅₍₂₁₎和G_5j(j=22，23)，G₅₍₂₂₎和G_5j(j=23，24，25)，G₅₍₂₄₎和G₅₍₂₅₎都分别不是共第二immanant的.

同样地，根据表 1，解方程τ(G₅₀)-τ(G_5j)=0(j=4，5，7，9，10，12，13，24，25)，τ(G₅₁)-τ(G_5j)= 0(j=10，20)，τ(G₅₂)-τ(G_5j)=0(j=10，20)，τ(G₅₃)-τ(G_5j)=0(j=10，12，13，20)，τ(G₅₄)-τ(G_5j)=0(j= 9，10，12，14，15，16，17，19，20，21，23)，τ(G₅₅)-τ(G_5j)=0(j=10，14，15，16，17，19，21)，τ(G₅₆)-τ(G_5j)=0(j=10，12，14，20)，τ(G₅₇)-τ(G_5j)=0(j=9，15，16，21，23)，τ(G₅₈)-τ(G_5j)=0(j=10，12，20)，τ(G₅₉)-τ(G_5j)=0(j=15，16，17，19，20，21，23)，τ(G₅₍₁₀₎)-τ(G_5j)=0(j=11，13，14，17，18，19，20，22，24，25)，τ(G₅₍₁₁₎)-τ(G₅₍₂₀₎)=0，τ(G₅₍₁₂₎)-τ(G_5j)=0(j=15，16，17，19，20，21，23，24)，τ(G₅₍₁₃₎)-τ(G_5j)=0(j=15，16，17，19，20，21，23)，τ(G₅₍₁₄₎)-τ(G_5j)=0(j=20，24)，τ(G₅₍₁₅₎)-τ(G_5j)=0(j=24，25)，τ(G₅₍₁₆₎)-τ(G_5j)=0(j=20，24，25)，τ(G₅₍₁₇₎)-τ(G_5j))=0(j=24，25)，τ(G₅₍₁₉₎)-τ(G_5j)=0(j= 20，24，25)，τ(G₅₍₂₀₎)-τ(G_5j)=0(j=21，22，23，25)，τ(G₅₍₂₁₎)-τ(G_5j)=0(j=24，25)和τ(G₅₍₂₃₎)-τ(G_5j)=0(j=24，25). 我们可以得到这些方程或者没有解，或者没有整数根. 因此，G₅₀和G_5j(j=4，5，7，9，10，12，13，24，25)，G₅₁和G_5j(j=10，20)，G₅₂和G_5j(j=10，20)，G₅₃和G_5j(j=10，12，13，20)，G₅₄和G_5j(j=9，10，12，14，15，16，17，19，20，21，23)，G₅₅和G_5j(j=10，14，15，16，17，19，21)，G₅₆和G_5j(j=10，12，14，20)，G₅₇和G_5j(j=9，15，16，21，23)，G₅₈和G_5j(j=10，12，20)，G₅₉和G_5j(j=15，16，17，19，20，21，23)，G₅₍₁₀₎和G_5j(j=11，13，14，17，18，19，20，22，24，25)，G₅₍₁₁₎和G₅₍₂₀₎，G₅₍₁₂₎和G_5j(j=15，16，17，19，20，21，23，24)，G₅₍₁₃₎和G_5j(j=15，16，17，19，20，21，23)，G₅₍₁₄₎和G_5j(j=20，24)，G₅₍₁₅₎和G_5j(j=24，25)，G₅₍₁₆₎和G_5j(j=20，24，25)，G₅₍₁₇₎和G_5j(j=24，25)，G₅₍₁₉₎和G_5j(j=20，24，25)，G₅₍₂₀₎和G_5j(j=21，22，23，25)，G₅₍₂₁₎和G_5j(j=24，25)，G₅₍₂₃₎和G_5j(j=24，25) 都分别不是共第二immanant的.

由引理2和上述探讨可知，G₅₀，G₅₁，G₅₂，G₅₃，G₅₄，G₅₅，G₅₆，G₅₇，G₅₈，G₅₉，G₅₍₁₀₎，G₅₍₁₁₎，G₅₍₁₂₎，G₅₍₁₃₎，G₅₍₁₄₎，G₅₍₁₅₎，G₅₍₁₆₎，G₅₍₁₇₎，G₅₍₁₈₎，G₅₍₁₉₎，G₅₍₂₀₎，G₅₍₂₁₎，G₅₍₂₂₎，G₅₍₂₃₎，G₅₍₂₄₎和G₅₍₂₅₎是由d₂-多项式确定的.

结合定理2-定理6，定理1得证.

非同构的图有相同的immanantal多项式的例子已经被给了出来. 因此，刻画由d₂-多项式确定的图是一个有趣的问题. 本文证明了所有的几乎完全图都是由d₂-多项式确定的. 另外，我们发现两个值得进一步研究的问题：

问题1  证明图K_n-E(K_1，s)和K_n-E(pK₂)是由d₂-多项式确定的，其中$ s \leqslant n-2 \text { 和 } p \leqslant \frac{n}{2} $.

问题2  构造一个从完全图K_n中删除l条边得到的图对，使得它们是共第二immanant的.