高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

在Cd(0001)基底上外延生长单原子层锗

,  ,  ,  ,  , 

上一篇

下一篇

王浩, 李佐, 杨孝天, 等. 在Cd(0001)基底上外延生长单原子层锗[J]. 西南师范大学学报(自然科学版), 2023, 48(8): 55-62. doi: 10.13718/j.cnki.xsxb.2023.08.007
引用本文: 王浩, 李佐, 杨孝天, 等. 在Cd(0001)基底上外延生长单原子层锗[J]. 西南师范大学学报(自然科学版), 2023, 48(8): 55-62. doi: 10.13718/j.cnki.xsxb.2023.08.007
shu
WANG Hao, LI Zuo, YANG Xiaotian, et al. Epitaxial Growth of Single Atomic Layer Germanium on Cd (0001) Substrate[J]. Journal of Southwest China Normal University(Natural Science Edition), 2023, 48(8): 55-62. doi: 10.13718/j.cnki.xsxb.2023.08.007
Citation: WANG Hao, LI Zuo, YANG Xiaotian, et al. Epitaxial Growth of Single Atomic Layer Germanium on Cd (0001) Substrate[J]. Journal of Southwest China Normal University(Natural Science Edition), 2023, 48(8): 55-62. doi: 10.13718/j.cnki.xsxb.2023.08.007
shu

在Cd(0001)基底上外延生长单原子层锗

  • 西南大学 物理科学与技术学院, 重庆 400715

  • 基金项目: 国家自然科学基金项目(11874304, 11574253)
详细信息
    作者简介:

    王浩, 硕士研究生, 主要从事纳米结构与表面界面物理研究 .

    通讯作者: 王俊忠, 教授, 硕士研究生导师

  • 中图分类号: O469

Epitaxial Growth of Single Atomic Layer Germanium on Cd (0001) Substrate

  • School of Physical Science and Technology, Southwest University, Chongqing 400715, China

  • 摘要:

    利用超高真空-低温扫描隧道显微镜(STM)技术和密度泛函理论(DFT)研究了锗(Ge)在Cd(0001)表面的薄膜生长行为和电子性质.研究发现室温下沉积在Cd(0001)表面上的Ge原子容易形成纳米尺度的团簇.当Cd衬底的温度降至100 K左右, Ge原子形成单原子层厚的二维薄膜.高分辨的STM图表明Ge的单原子层具有1×1的赝晶结构.扫描隧道谱(STS)测量发现Ge的单原子层表现出金属性行为.DFT计算结果表明: Ge原子优先占据Cd(0001)衬底的六角密排空位, Ge与Cd(0001)衬底之间存在静电作用, Ge原子之间通过共价键相结合.

    Abstract:

    The growth behavior and electronic properties of germanium (Ge) on the Cd (0001) surface have been studied by ultra-high vacuum low-temperature scanning tunneling microscopy and density functional theory. It was found that Ge atoms deposited on the surface of Cd (0001) at room temperature readily form nanoscale clusters. The Ge atoms formed a two-dimensional film with a single atomic layer thickness as the temperature of the Cd substrate was lowered to about 100 K. The high-resolution STM map showed that the monatomic layer of Ge has a 1? pseudocrystalline structure. Scanning tunneling spectroscopy (STS) measurements revealed that the monoatomic layers of Ge exhibit metallic behavior. The results of the DFT calculation showed that Ge atoms preferentially occupy the hexagonal close empty position of the Cd (0001) substrate, there was an electrostatic interaction between Ge and Cd (0001) substrate, and Ge atoms were combined by a covalent bond.

  • 加载中

  • 图 1  Cd(0001)衬底的STM图与原子模型图

    下载: 全尺寸图片 幻灯片

    图 2  Cd(0001)表面上的Ge原子单层的STM图

    下载: 全尺寸图片 幻灯片

    图 3  在二维Ge岛上采集的扫描隧道谱

    下载: 全尺寸图片 幻灯片

    图 4  DFT计算的Ge原子单层的结构模型及电子性质

    下载: 全尺寸图片 幻灯片

    表 1  理论计算Ge在Cd(0001)上的吸附能、Cd-Ge原子层距离、Ge-Ge原子键长

    吸附位 吸附能/eV Cd-Ge原子层距离/nm Ge-Ge键长/nm
    Top -0.53 0.240 0.282
    Bridge -0.56 0.249 0.311
    Fcc-hollow -0.55 0.243 0.311
    Hcp-hollow -0.58 0.242 0.311
    下载: 导出CSV
  • [1] DEPUYDT B, THEUWIS A, ROMANDIC I. Germanium: From the First Application of Czochralski Crystal Growth to Large Diameter Dislocation-Free Wafers [J]. Materials Science in Semiconductor Processing, 2006, 9(4-5): 437-443. doi: 10.1016/j.mssp.2006.08.002
    [2] 宗明吉. 三代半导体材料构成光子晶体能态密度的研究[J]. 激光与红外, 2010, 40(8): 892-895. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JGHW201008023.htm
    [3] NOVOSELOV K S, GEIM A K, MOROZOV S V, et al. Two-Dimensional Gas of Massless Dirac Fermions in Graphene [J]. Nature, 2005, 438(7065): 197-200. doi: 10.1038/nature04233
    [4] TSE W K, QIAO Z H, YAO Y G, et al. Quantum Anomalous Hall Effect in Single-Layer and Bilayer Graphene [J]. Physical Review B, 2011, 83(15): 155447. doi: 10.1103/PhysRevB.83.155447
    [5] BERGER C, SONG Z M, LI X B, et al. Electronic Confinement and Coherence in Patterned Epitaxial Graphene [J]. Science, 2006, 312(5777): 1191-1196. doi: 10.1126/science.1125925
    [6] NOVOSELOV K S, GEIM A K, MOROZOV S V, et al. Electric Field Effect in Atomically Thin Carbon Films [J]. Science, 2004, 306(5696): 666-669. doi: 10.1126/science.1102896
    [7] ZHANG Y B, TAN Y W, STORMER H L, et al. Experimental Observation of the Quantum Hall Effect and Berry's Phase in Graphene [J]. Nature, 2005, 438(7065): 201-204. doi: 10.1038/nature04235
    [8] MUZYCHENKO D A, ORESHKIN S I, PANOV V I, et al. Single and Multi Domain Buckled Germanene Phases on Al(111) Surface [J]. Nano Research, 2019, 12(12): 2988-2996. doi: 10.1007/s12274-019-2542-1
    [9] ZHUANG J C, LIU C, ZHOU Z Y, et al. Dirac Signature in Germanene on Semiconducting Substrate [J]. Advanced Science, 2018, 5(7): 1800207. doi: 10.1002/advs.201800207
    [10] 秦志辉. 类石墨烯锗烯研究进展[J]. 物理学报, 2017, 66(21): 17-24. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201721003.htm
    [11] YAO Y G, YE F, QI X L, et al. Spin-Orbit Gap of Graphene: First-Principles Calculations [J]. Physical Review B, 2007, 75(4): 041401.
    [12] LIU C C, JIANG H A, YAO Y G. Low-Energy Effective Hamiltonian Involving Spin-Orbit Coupling in Silicene and Two-Dimensional Germanium and Tin [J]. Physical Review B, 2011, 84(19): 195430. doi: 10.1103/PhysRevB.84.195430
    [13] XU M S, LIANG T, SHI M M, et al. Graphene-Like Two-Dimensional Materials [J]. Chemical Reviews, 2013, 113(5): 3766-3798. doi: 10.1021/cr300263a
    [14] CAHANGIROV S, TOPSAKAL M, AKTVRK E, et al. Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium [J]. Physical Review Letters, 2009, 102(23): 236804. doi: 10.1103/PhysRevLett.102.236804
    [15] ROOME N J, CAREY J D. Beyond Graphene: Stable Elemental Monolayers of Silicene and Germanene [J]. ACS Applied Materials & Interfaces, 2014, 6(10): 7743-7750.
    [16] NIJAMUDHEEN A, BHATTACHARJEE R, CHOUDHURY S, et al. Electronic and Chemical Properties of Germanene: The Crucial Role of Buckling [J]. The Journal of Physical Chemistry C, 2015, 119(7): 3802-3809. doi: 10.1021/jp511488m
    [17] SCALISE E, HOUSSA M, POURTOIS G, et al. Vibrational Properties of Silicene and Germanene [J]. Nano Research, 2013, 6(1): 19-28. doi: 10.1007/s12274-012-0277-3
    [18] LIU C C, FENG W X, YAO Y G. Quantum Spin Hall Effect in Silicene and Two-Dimensional Germanium [J]. Physical Review Letters, 2011, 107(7): 076802. doi: 10.1103/PhysRevLett.107.076802
    [19] YE X S, SHAO Z G, ZHAO H B, et al. Intrinsic Carrier Mobility of Germanene is Larger than Graphene's: First-Principle Calculations [J]. RSC Advances, 2014, 4(41): 21216-21220. doi: 10.1039/C4RA01802H
    [20] DÁVILA M E, XIAN L, CAHANGIROV S, et al. Germanene: a Novel Two-Dimensional Germanium Allotrope Akin to Graphene and Silicene [J]. New Journal of Physics, 2014, 16(9): 095002. doi: 10.1088/1367-2630/16/9/095002
    [21] ZHUANG J C, GAO N, LI Z, et al. Cooperative Electron–Phonon Coupling and Buckled Structure in Germanene on Au(111) [J]. ACS Nano, 2017, 11(4): 3553-3559. doi: 10.1021/acsnano.7b00687
    [22] BUI N N, LEDINA M, REBER T J, et al. Electrochemical Scanning Tunneling Microscopic Study of the Potential Dependence of Germanene Growth on Au(111) at pH 9. 0 [J]. ACS Nano, 2017, 11(9): 9481-9489. doi: 10.1021/acsnano.7b05236
    [23] LIN C-H, HUANG A, PAI W W, et al. Single-layer dual germanene phases on Ag(111) [J]. Physical Review Materials, 2018, 2(2): 024003-1-024003-8.
    [24] QIN Z H, PAN J B, LU S Z, et al. Direct Evidence of Dirac Signature in Bilayer Germanene Islands on Cu(111) [J]. Advanced Materials, 2017, 29(13): 1606046. doi: 10.1002/adma.201606046
    [25] LI L F, LU S Z, PAN J B, et al. Buckled Germanene Formation on Pt(111) [J]. Advanced Materials, 2014, 26(28): 4820-4824. doi: 10.1002/adma.201400909
    [26] MUZYCHENKO D A, ORESHKIN A I, LEGEN'KA A D, et al. Atomic Insights into Single-Layer and Bilayer Germanene on Al(111) Surface [J]. Materials Today Physics, 2020, 14: 100241. doi: 10.1016/j.mtphys.2020.100241
    [27] YAN F N, XU S G, HE C, et al. Identifying the Alloy Structures of Germanene Grown on Al(111) [J]. Physical Review B, 2022, 106(7): 075405. doi: 10.1103/PhysRevB.106.075405
    [28] EDWARDS D A, WALLACE W E, CRAIG R S. Magnesium-Cadmium Alloys. Ⅳ. the Cadmium-Rich Alloys; Some Lattice Parameters and Phase Relationships between 25 and 300°. Structure of the MgCd3 Superlattice. Schottky Defects and the Anomalous Entropy1 [J]. Journal of the American Chemical Society, 1952, 74(21): 5256-5261. doi: 10.1021/ja01141a006
    [29] HAHN E, KAMPSHOFF E, WÄLCHLI N, et al. Strain Driven FCC-Bct Phase Transition of Pseudomorphic Cu Films on Pd(100) [J]. Physical Review Letters, 1995, 74(10): 1803-1806. doi: 10.1103/PhysRevLett.74.1803
    [30] PRATZER M, ELMERS H J, GETZLAFF M. Heteroepitaxial Growth of Co on W(110) Investigated by Scanning Tunneling Microscopy [J]. Physical Review B, 2003, 67(15): 153405. doi: 10.1103/PhysRevB.67.153405
    [31] SAVIN A, JEPSEN O, FLAD J, et al. Electron Localization in Solid-State Structures of the Elements: The Diamond Structure [J]. Angewandte Chemie International Edition in English, 1992, 31(2): 187-188. doi: 10.1002/anie.199201871
    [32] SAVIN A, NESPER R, WENGERT S, et al. ELF: The Electron Localization Function [J]. Angewandte Chemie International Edition in English, 1997, 36(17): 1808-1832. doi: 10.1002/anie.199718081
    [33] BECKE A D, EDGECOMBE K E. A Simple Measure of Electron Localization in Atomic and Molecular Systems [J]. The Journal of Chemical Physics, 1990, 92(9): 5397-5403. doi: 10.1063/1.458517
  • 加载中
图( 4) 表( 1)
计量
  • 文章访问数:  5103
  • HTML全文浏览数:  5103
  • PDF下载数:  217
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-02-18
  • 刊出日期:  2023-08-20

在Cd(0001)基底上外延生长单原子层锗

    通讯作者: 王俊忠, 教授, 硕士研究生导师
    作者简介: 王浩, 硕士研究生, 主要从事纳米结构与表面界面物理研究
  • 西南大学 物理科学与技术学院, 重庆 400715
  • 收稿日期:  2023-02-18
基金项目:  国家自然科学基金项目(11874304, 11574253)

摘要: 

利用超高真空-低温扫描隧道显微镜(STM)技术和密度泛函理论(DFT)研究了锗(Ge)在Cd(0001)表面的薄膜生长行为和电子性质.研究发现室温下沉积在Cd(0001)表面上的Ge原子容易形成纳米尺度的团簇.当Cd衬底的温度降至100 K左右, Ge原子形成单原子层厚的二维薄膜.高分辨的STM图表明Ge的单原子层具有1×1的赝晶结构.扫描隧道谱(STS)测量发现Ge的单原子层表现出金属性行为.DFT计算结果表明: Ge原子优先占据Cd(0001)衬底的六角密排空位, Ge与Cd(0001)衬底之间存在静电作用, Ge原子之间通过共价键相结合.

English Abstract

    全文HTML

  • 锗(Ge)是介于硅和锡之间的第Ⅳ主族元素，也是一种典型的半导体材料. Si和Ge是第一代半导体材料，后来由于硅基材料的兴起导致Ge逐渐被取代[1-2]. 自2004年石墨烯被发现以来，其特殊的电子性质引起了人们的广泛关注[3]，如极高的电子速度和迁移率、量子反常霍尔效应等[4-6]. 由于其特殊的成键方式，以及电子作为无质量的狄拉克费米子，石墨烯的应用前景非常广阔[7-9]. 但是石墨烯没有带隙，即使在自旋轨道耦合作用下石墨烯打开的能隙也非常小(约10-3eV)，这严重制约了其在电子器件领域的应用[10-12]. 因此，寻找具有较大能隙的二维原子晶体材料，如与碳元素位于同一主族的Si，Ge和Sn的单原子层，成为目前研究的热点课题[13].

    CAHANGIROV等[14]通过DFT计算预言，Ge原子也可形成类似石墨烯的稳定蜂窝结构，其电子性质与石墨烯类似，都属于二维拓扑绝缘体和无质量的狄拉克费米子体系. 人们把这种具有类蜂窝结构的Ge原子层称为锗烯(Germanene). 与平整的石墨烯不同的是，锗烯的蜂窝结构具有一定的翘曲，蜂窝上的6个Ge原子交替出现在两个不同的高度上[15-17]. 锗烯的翘曲结构使得Ge原子之间的自旋轨道耦合作用更强，在费米能级处可以打开一个较大的能隙(约24 meV)，该能隙远远大于石墨烯的能隙[18]. 这种较大的拓扑绝缘体能隙有利于实现体态与量子边缘态的分离(避免电子输运过程中体态的混入)，有效降低电子器件的能耗；此外，理论预测的锗烯载流子迁移率略低于石墨烯[19]. 因此高温量子霍尔效应有望在锗烯中实现[18]. 但是锗烯无法像石墨烯那样通过机械剥离(如用胶带撕扯)的方法获得，于是如何获得自由的锗烯单层成为一个难题. 目前人们开始尝试采用分子束外延的方法来外延生长锗烯，但要想获得自由的锗烯需要一个合适的基底. 到目前为止，实验报道的外延锗烯的基底材料有：Au(111)[20-22]、Ag(111)[23]、Cu(111)[24]、Pt(111)[25]、Al(111)[26]等. 这些金属衬底大多会与锗形成合金，并且关于锗烯的结构模型还存在争论[27]，因此仍需要继续寻找合适的衬底材料来生长锗烯.

    本研究采用分子束外延法在Cd(0001)基底上外延生长Ge原子单层薄膜. 选择Cd(0001)表面为基底的原因是Cd的电负性较小，不易转移电子. 实验发现：室温沉积的Ge原子很容易在Cd(0001)表面形成纳米尺度的团簇. 当改用低温沉积(~100 K)，Ge原子则会形成单原子层厚的二维薄膜. 高分辨的STM图表明Ge单原子层具有1×1的赝晶结构，这说明Ge原子层中存在一定的应力. 扫描隧道谱(STS)测量发现Ge的单原子层具有金属性行为. DFT计算结果发现Ge原子优先占据Cd(0001)衬底的六角密排空位，Ge与Cd(0001)衬底之间存在静电作用，Ge原子之间通过共价键相结合.

1.   实验与理论计算

    1.1.   实验部分

  • 本研究的实验是在日本Unisoku公司生产的超高真空低温扫描隧道显微镜(LT-STM)系统上完成的，系统的本底真空度为2.7×10-8 Pa. 实验所用的Cd(0001)基底是生长在Si(111)-7×7上厚度为15~20原子单层(monolayer，ML) 的Cd薄膜. 为获得洁净的Si(111)-7×7表面，先将Si(111)样品升温至800 K进行除气. 然后通过快闪的方法将样品升温至1 500 K，以除去表面的氧化层. 将放置于氮化硼坩埚中的镉丝加热至400 K，使Cd原子沉积到Si(111)-7×7表面，由此得到高质量的Cd(0001)薄膜. 随后将纯度为99.999 9%的锗加热至1 280 K，使之沉积到Cd(0001)表面，同时衬底的温度保持在室温或低温. 最后将样品传送到STM腔进行观察，观察腔温度保持在液氮(~78 K)温度.

    • 1.2.   理论计算

  • DFT计算采用广义梯度近似方法(GGA)中的Perdew-Becke-Ernerhof(PBE)泛函. 计算模拟的衬底由3层Cd原子组成的3×3超胞构成. 为有效模拟实际Cd(0001)衬底，固定最底层的Cd原子；为减小原子层间不必要的相互作用，建立2 nm厚的真空层. 在Cd(0001)表面放置9个Ge原子，对应单层Ge的3×3超胞，以此模拟Cd(0001)表面上的Ge原子的六角密排结构. 在计算中，平面波的截断能选取570 eV，设置为3×3×1的k-meshes网格点作为倒空间中的积分点数. 将每个原子的Hellmann-Feynman力优化到小于0.3 eV/nm和总能量优于10-5 eV作为收敛标准.

2.   结果与讨论

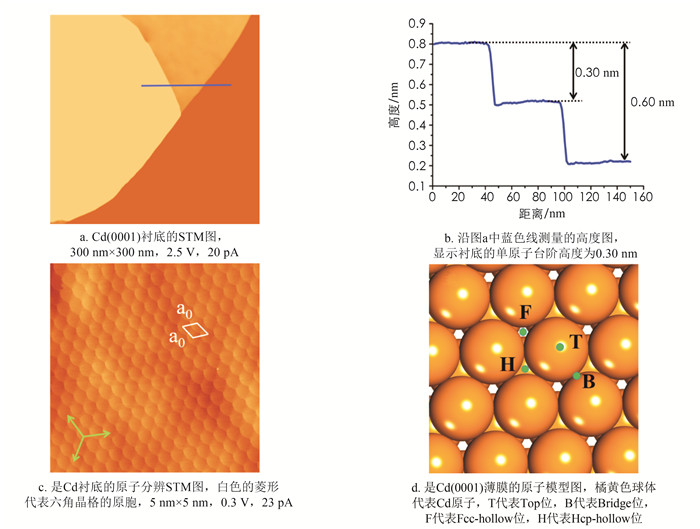
  • 图 1a是制备的光滑平整的Cd(0001)薄膜的STM图. 从中可以看出Cd薄膜的台阶宽度大约在200 nm左右，单原子台阶的高度(0.30±0.01) nm (图 1b)，接近于Cd单晶沿[0001]方向的面间距(0.281 nm)[28]. 图 1c为Cd薄膜原子分辨图，Cd原子按照六角密排方式进行排列，其晶格常数为a0=(0.30±0.02) nm，与镉单晶(0001)面的晶格常数(0.298 nm)非常接近，且二者都具有六角对称性. 考虑到二维的薄膜相和三维的块体相之间的差异，实验制备的二维薄膜可以认为是晶态的Cd(0001)薄膜. 图 1d展示了Ge原子在Cd(0001)表面上四个可能的吸附位，它们分别是顶位(T)、桥位(B)、面心立方位(F)和六角密排位(H).

    首先，把少量的Ge原子(覆盖度θ = 0.2 ML)沉积到处于室温的Cd(0001)基底上. STM扫描发现衬底台面上的Ge原子既能聚集成纳米尺度的团簇，也能形成单原子层厚的二维岛(图 2a). 统计分析表明，在衬底台面上形成的Ge团簇的平均直径为9.7 nm. 但是，在衬底台阶附近的Ge团簇的尺寸比较小(直径在5 nm左右). 图 2b是沿着图 2a中的蓝色线段所作的高度剖面图，不难发现Ge原子层的高度为(0.28±0.01) nm，略低于Cd衬底的台阶高度.

    为了制备高质量的Ge原子层，尽可能避免Ge原子聚集成团簇，把衬底的温度降至100 K左右(低温沉积法)，以此降低Ge原子的表面扩散长度. 图 2c展示了覆盖度为0.7 ML的Ge薄膜的形貌图. 大部分的衬底表面被平整的Ge原子层覆盖，同时Ge原子层表面有很多较小的原子团簇. 通过对大量Ge原子层的统计平均发现，Ge原子层畴区的平均尺寸为~170 nm. 图 2d是Ge原子层的原子分辨STM图，不难看出Ge原子的排列方式与Cd(0001)表面一样，都具有六角对称的晶格结构. 更重要的是，二者的晶格常数(0.30 nm)和晶格方向也完全一样. 也就是说Ge原子层相对于衬底表现出1×1的赝晶结构. 根据薄膜生长理论，赝晶结构存在于较低的晶格失配薄膜中. 在异质外延过程中薄膜的结构通常不同于体相材料，这就是所谓的亚稳态的薄膜相. 这些新相可能表现出新的物理和化学性质. 在外延生长过程中，晶格失配引起的弹性应变极大地影响了薄膜的生长方式. 当晶格失配较小时，弹性应变能可以通过赝晶生长的形式调节，使得薄膜原子的横向排列周期与衬底相同，但垂直方向的周期则不同于衬底. 当晶格失配较大时，则会在薄膜/衬底的界面上形成失配位错来缓解应变产生的能量[29-30].

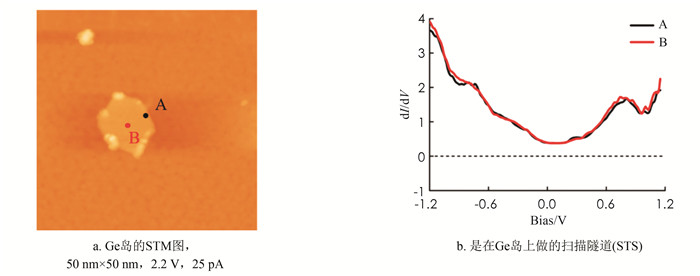
    为了研究Ge单原子层的电子性质，在直径约10 nm的二维Ge岛上采集了STS谱，做谱位置选择在岛的边缘和中间位置(图 3a). 做谱的准确性取决于针尖的洁净程度和针尖高度的稳定性. 本研究在Ge岛上做了大量的STS谱，得到重复性较好的结果. 为了便于比较在Ge岛上不同位置做的谱，将得到两条STS谱一起放到图 3中. 黑色谱线A是在岛边缘位置上采集的，红色谱线B是在岛的中央位置采集的. 可以看到两条线重合得比较好，在费米能级(V=0)微分电导不是0，这因为着针尖下方的Ge原子层的电子态密度(density of states，DOS)在费米能级处是一个非零的有限值，因为STM理论告诉我们隧道谱采集的微分电导正比于样品的DOS. 因此可以判断实验制备的Ge单原子层薄膜具有金属性行为.

    为了深入理解上述实验结果，利用DFT理论计算了Ge原子在Cd(0001)表面上的4种不同位置的吸附能、Cd-Ge原子层距离、Ge-Ge键长. 单个Ge原子吸附能(Eads)的计算方法是分别计算几个体系的能量：Ge原子与Cd(0001)超胞组成体系的总能量(ETotal)、计算自由Ge原子层总能量(EGe)、自由Cd(0001)总能量(ECd(0001))，按照下面公式进行计算：

    其中n代表Ge原子的个数. 理论计算结果表明Ge原子在六角密排位(Hcp-hollow)的吸附能最小(-0.58 eV)(表 1)，这说明Ge原子优先吸附在Cd(0001)表面上的H位，因为此时体系的能量最低. 理论计算还发现Cd-Ge原子层之间的距离在0.240~0.250 nm之间，其中在最稳定的H位两原子层间距离约0.242 nm，与实验观察得到Ge原子单层的高度(0.28 nm)有一定的差距. 理论计算的Ge-Cd距离是两个原子层间的几何高度，而STM测量的高度既有几何高度的贡献，同时也包含了样品电子态密度的贡献. 因此，STM测量的高度与几何高度并不严格一致，因此常被称为“视在高度(apparent height)”. 我们推测造成理论计算和实验测量之间的误差原因可以归因于样品和针尖的电子态对测量高度的影响，因为电子的隧穿过程不仅依赖于距离还依赖于针尖和样品的电子态密度的乘积. 吸附在H位Ge原子间键长理论计算值约为0.311 nm，而实验测得Ge薄膜的晶格常数约0.30 nm，两者误差为3. 6%，理论计算结果与实际测量数值比较吻合，说明本研究的理论计算结果可靠.

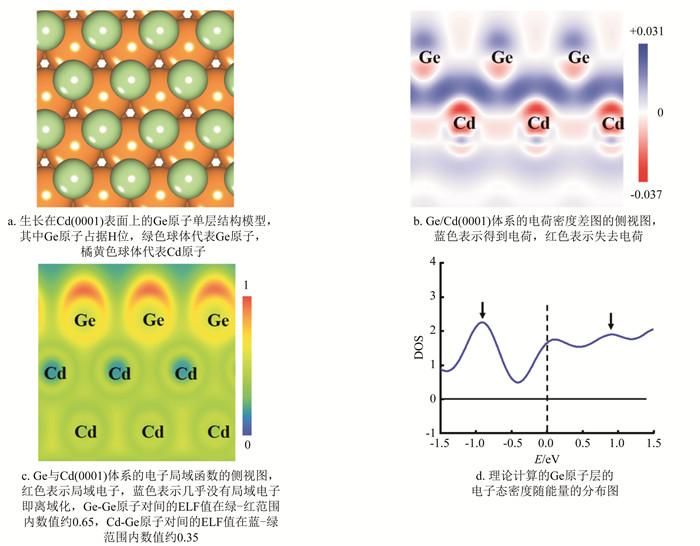
    图 4a是经过优化后的Ge原子单层的结构模型图，其中Ge原子占据衬底表面的H位. 理论计算的Ge原子单层与实验观测的1×1的赝晶结构完全一致. 在完成结构优化后，还计算了该体系电荷密度差(electron density difference，EDD)和电子局域化函数(electron localization function，ELF). 图 4b为体系的电荷密度差图，图中蓝色区域代表电子积累，红色区域代表失去电子，白色区域代表无得失电子. 图中可以观察到最上层Cd原子失去的电子最多，其中大部分电子聚集在Ge与Cd原子层之间，Cd向Ge原子层注入了0.031 e，转移的电荷量很少. 获得定域轨道的方法可用于判断分子甚至固体中化学键成分，而局域化轨道对于配位数较高的固体就会变得比较模糊，所以很少采用该方法[31]. 但是电子局域函数(ELF)可以做到可视化地判断固体、分子晶体中的化学键成分[32]. 为了判断Cd-Ge，Ge-Ge原子对之间是否成键，对Ge与Cd(0001)组成的体系计算了电子局域函数. 电子局域函数表达式由Edgecombe和Becke引入[33]，表示在某一位置电子附近找到与其有相同自旋电子的概率，即该电子局域化程度. ELF表达式为：

    其中γ(r)为：

    式中：K代表自旋相同电子对的概率密度，ρ(r)是r处电子密度，Kh是均匀电子气密度为ρ的K值. ELF的数值范围是0-1，ELF数值为1时表示在某一电子附近没有相同自旋电子，该电子孤立存在或成键，即该电子是局域的；ELF数值为0.5时为均匀电子气；ELF值为0时表示完全离域化. 对于Ge与Cd(0001)组成的体系计算结果如图 4c所示，从图中可以发现Cd-Ge原子之间的ELF值约为0.35，电子之间没有配对，表明Cd-Ge原子没有成键，因此Ge原子层与Cd(0001)面之间存在静电吸附作用；而Ge-Ge原子对之间的ELF约为0.65，表明Ge-Ge原子对之间形成共价结合. 所以Ge原子依靠静电吸附在Cd(0001)上，面内Ge原子之间依靠共价键形成较为稳定的六角密排结构. 此外，本研究还计算了Ge原子层的电子态密度(density of states，DOS)随能量的分布(图 4d). 不难看出，在费米能级(E=0)处有非零的DOS，表明Ge原子层具有金属性，这与实验测量的STS结果一致，此外，DOS曲线上存在两个电子态密度峰，分别位于-0.9 eV和+0.9 eV处，二者非常接近图 3b中STS曲线上的两个峰位(±0.8 eV).

3.   结论

  • 本研究采用分子束外延法和STM研究了Ge原子在Cd(0001)衬底上的薄膜生长. 实验发现，当生长温度为室温时，Ge原子在形成二维薄膜的同时也会形成纳米团簇，从而影响薄膜的质量. 当改用低温沉积时，Ge原子则形成光滑的单原子层薄膜，该薄膜具有1×1的赝晶结构，这表明Ge原子层中存在一定程度的应力. 通过STS谱发现Ge的赝晶结构具有金属特征. 此外，基于密度泛函理论计算了Ge原子层的结构和性质. 发现Ge原子的优先吸附位置为六角密排的H位. 根据电荷密度差和电子局域函数分析，Cd-Ge之间只存在静电吸附作用，而Ge-Ge之间以共价方式结合. 本研究结果为制备Ge超薄膜提供了一种可行方案.

参考文献 (33)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回