文献[1-3]在交换Noetherian环上分别以不同的称谓独立地引入了半对偶模的概念.交换Noetherian环上的半对偶模是对偶模和秩为1的自由模的共同推广.与对偶模不同的是, 半对偶模在一般环上是大量存在的.近些年来, 半对偶模及其相关模类受到了许多学者的广泛关注(参见文献[4-15]).

设C是交换Noetherian环R上的半对偶模, 文献[12]在交换Noetherian环上引入了C-Gorenstein投射、C-Gorenstein内射和C-Gorenstein平坦模类的概念, 并定义了模类的3种新的相对同调维数：C-Gorenstein投射维数、C-Gorenstein内射维数及C-Gorenstein平坦维数, 建立了这3种新的同调维数与环R关于C的平凡扩张上的Gorenstein同调维数的关系, 并对C-Gorenstein投射维数与R关于C的平凡扩张上的G-维数进行了对比.文献[13]又将C-Gorenstein投射模及C-Gorenstein投射维数的概念推广到了非交换Noetherian环的情形.

文献[5]讨论了环同态下C-Gorenstein同调模类的传递性质, 特别地, 在交换环S是平坦维数有限的R-代数的条件下证明了：如果A是C-Gorenstein平坦R-模, $\tilde F$是平坦S-模, 那么A⊗_R$\tilde F$是C⊗_RS-Gorenstein平坦S-模.文献[14]证明了：如果R是凝聚环, S是使得Gorenstein平坦S-模关于扩张封闭的满忠实平坦R-代数, 那么R-模M是Gorenstein平坦的当且仅当S-模S⊗_RM是Gorenstein平坦的.

受文献[14]的启发, 本文将证明下述结果, 它给出了文献[5]中定理的一个充分必要性结论：

定理1  设R是交换的凝聚环, S是使得C⊗_RS-Gorenstein平坦S-模关于扩张封闭的满忠实平坦交换R-代数, 则R-模M是C-Gorenstein平坦的当且仅当S-模S⊗_RM是C⊗_RS-Gorenstein平坦的.

本文中, 都假定R是交换环.根据文献[5], 我们有：

引理1  设S是交换环, φ：R→S是fd_RS＜∞的环同态.则C⊗_RS是半对偶S-模.

引理2  以下条件等价：

(ⅰ) X是C-平坦R-模；

(ⅱ)对任意的内射R-模E, Hom_R(X, E)是C-内射R-模；

(ⅲ)对任意的内射余生成子E, Hom_R(X, E)是C-内射R-模.

证  (ⅰ)⇒(ⅱ)和(ⅱ)⇒(ⅲ)是显然的.

(ⅲ)⇒(ⅰ)要证X是C-平坦的, 根据文献[8]的引理5.2, 只需说明X∈$\mathscr{B}$_C且Hom_R(C, X)是平坦R-模.因为Hom_R(X, E)是C-内射R-模, 所以Hom_R(X, E)∈$\mathscr{A}$_C.由文献[8]的命题7.2可知X∈$\mathscr{B}$_C.要证Hom_R(C, X)是平坦的, 根据文献[15]的定理3.2.9, 只需说明Hom_$\mathbb{Z}$(Hom_R(C, X), $\mathbb{Q}$/$\mathbb{Z}$)是内射的即可.而

并且根据(ⅲ)可知Hom_$\mathbb{Z}$(X, $\mathbb{Q}$/$\mathbb{Z}$)是C-内射的, 所以C⊗_RHom_$\mathbb{Z}$(X, $\mathbb{Q}$/$\mathbb{Z}$))是内射的, 从而Hom_$\mathbb{Z}$(Hom_R(C, X), $\mathbb{Q}$/$\mathbb{Z}$)是内射的.

引理3  对R-模M, 以下条件等价：

(ⅰ) M是$\mathscr{G}$_C-平坦R-模.

(ⅱ) M满足两条成立：

(a) $\mathscr{I}$_C┬M；

(b) 如果存在R-模的正合序列0→M→C⊗_RF⁰→C⊗_RF¹→…, 使得对所有的i∈$\mathbb{N}$, Fⁱ是平坦的, 并且对所有的内射R-模I, Hom_R(C, I)⊗_R-是正合的.

(ⅲ)存在R-模的短正合列0→M→G⊗_RF→G→0, 其中F是平坦的, G是$\mathscr{G}$_C-平坦的.

引理4  设0→C⊗_RF→G→H→0是R-模的短正合列.如果F是平坦的(即C⊗_RF是C-平坦的), G是$\mathscr{G}$_C-平坦的, 并且Hom_$\mathbb{Z}$(H, $\mathbb{Q}$/$\mathbb{Z}$)是$\mathscr{G}$_C-内射的, 那么H是$\mathscr{G}$_C-平坦的.

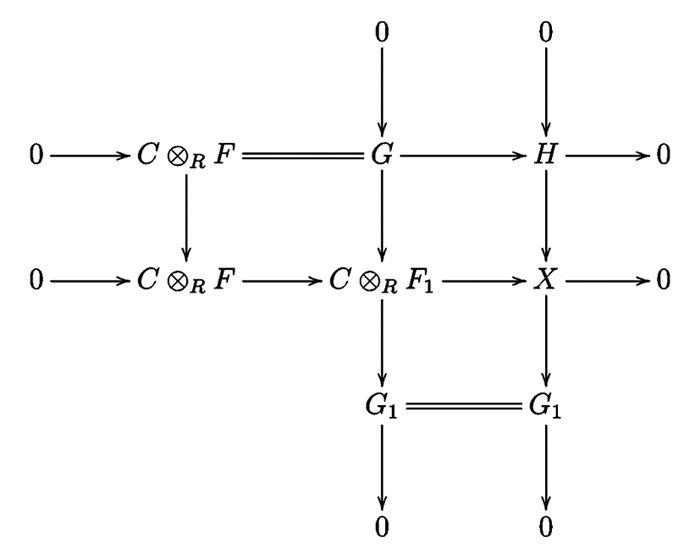
证  因为G是$\mathscr{G}$_C-平坦的, 所以存在短正合列0→G→G⊗_RF₁→G₁→0, 其中F₁是平坦的, G₁是$\mathscr{G}$_C-平坦的.考虑推出图

因为0→H→X→G₁→0正合, 所以0→G₁⁺→X⁺→H⁺→0正合.而G₁是$\mathscr{G}$_C-平坦的, 故G₁⁺是$\mathscr{G}$_C-内射的.又因H⁺是$\mathscr{G}$_C-内射的, 从而X⁺是$\mathscr{G}$_C-内射的.

由0→C⊗_RF→C⊗_RF₁→X→0的正合性可知, 0→X⁺→(C⊗_RF₁)⁺→(C⊗_RF)⁺→0是正合的.由于(C⊗_RF₁)⁺与(C⊗_RF)⁺都是C-内射的, 故X⁺的C-内射维数不大于1, 从而X⁺是C-内射的.根据引理2可知, X是C-平坦的.

最后, 考虑正合列0→H→X→G₁→0.因为X是C-平坦的, G₁⁺是$\mathscr{G}$_C-平坦的, 所以由文献[4]的引理2.11可知, H是$\mathscr{G}$_C-平坦的.证毕.

设R与S是交换环, C是半对偶R-模.为了区别R-模与S-模, 我们在记S-模时加~, 如$\tilde N$表示一个S-模.由引理1可知, 当S是满忠实R-代数时, C⊗_SS是半对偶S-模.在本文的剩余部分, 记C⊗_SS为$\tilde C$.

设S是满忠实平坦R-代数.则有纯正合列

且S/R是平坦R-模.用函子Hom_R(-, Hom_R(C, I))作用正合列(1), 因为S/R∈$\mathscr{A}$_C, 由文献[6]的引理2.3可知, $\mathscr{A}$_C⊥$\mathscr{I}$_C, 所以有短正合列

注意到：

(a) Hom_R(S, Hom_R(C, I))是$\tilde C$-内射S-模；

(b) 短正合列(2)可裂.

对(a), 由文献[5]的命题3.3可得.对(b), 根据文献[5]的命题3.1, Hom_R(S/R, Hom_R(C, I))是C-内射R-模, 再由于Hom_R(C, I)∈$\mathscr{A}$_C且$\mathscr{A}$_C⊥$\mathscr{I}$_C, 故Hom_R(C, I)⊥Hom_R(S/R, Hom_R(C, I)).从而正合列(2)可裂.这意味着, 任何一个C-内射R-模都是某个$\tilde C$-内射S-模的直和项.

引理5  设S是满忠实平坦R-代数.对任意的R-模M, 以下结论等价：

(ⅰ)对所有的i>0与每个内射R-模I, Tor_i^R(Hom_R(C, I), M)= 0；

(ⅱ)对所有的i>0与每个内射S-模J, Tor_i^S(Hom_S(C⊗_RS, J), S⊗_RM)= 0.

证  注意到, 对所有的i>0与每个S-模$\tilde X$, 都有Tor_i^S($\tilde X$, S⊗_RM)$ \cong $Tor_i^R($\tilde X$, M).

(ⅰ)⇒(ⅱ)  对任意的内射S-模$\tilde J$, 有

由于Tor_i^R(Hom_R(C, $\tilde J$), M)= 0, 故Tor_i^S(Hom_S(C⊗_RS, $\tilde J$), S⊗_RM)= 0.

(ⅱ)⇒(ⅰ)  因为每个C-内射R-模Hom_R(C, I)都是每个$\tilde C$-内射S-模的直和项, 所以要证Tor_i^R(Hom_R(C, I), M)=0, 只需证Tor_i^R(Hom_S(C⊗_RS, J), M)=0即可.而

由于Tor_i^S(Hom_S(C⊗_RS, J), S⊗_RM)=0, 故Tor_i^R(Hom_S(C⊗_RS, J), M)=0, 从而Tor_i^R(Hom_R(C, I), M)=0.

定理1的证明  必要性  根据文献[5]的命题4.12即得.

充分性  假设S⊗_RM是$\mathscr{G}$_{$\tilde C$}-平坦S-模.则对任意的内射S-模$\tilde J$, 有

故由引理5可知, 对任意的内射R-模I, 有

根据文献[2]的引理2.11, 我们还需要证明：存在正合列

使得每个Fⁱ是平坦的, 并且对任意的内射R-模I, 仍Hom_R(C, I)⊗_R-正合.

因为R是凝聚环, 所以$\mathscr{F}$_C是预包络类.故存在态射φ：M→C⊗_RF⁰, 其中F⁰是平坦的.又因为S⊗_RM是$\mathscr{G}$_{$\tilde C$}-平坦的, 所以S⊗_RM可嵌入到一个$\tilde C$-平坦模中.而

是纯正合的, 故

是正合的, 从而M又可以嵌入到S⊗_RM中, 因此M可以嵌入到$\tilde C$⊗_S$\tilde F$中.由于

每个平坦S-模是平坦R-模, 故C⊗_R$\tilde F$是C-平坦R-模, 从而M可以嵌入到C-平坦R-模中, 这就证明了φ是单射, 因此存在短正合列

首先要证明对任意的内射R-模I, Hom_R(C, I)⊗η是正合的, 只需证Hom_$\mathbb{Z}$(Hom_R(C, I)⊗η, $\mathbb{Q}$/$\mathbb{Z}$)正合.易得

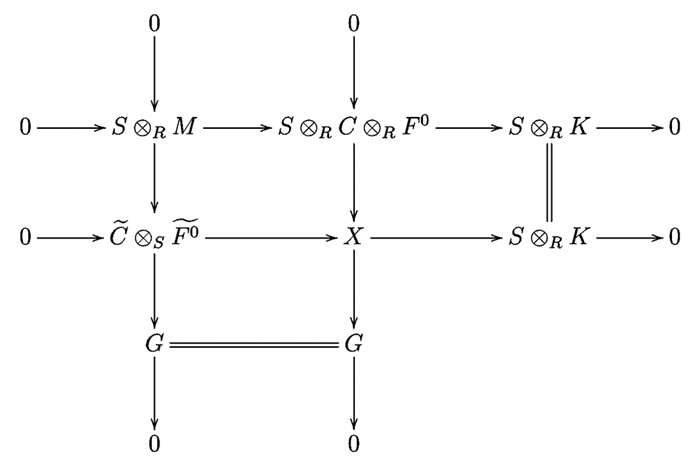
因为Hom_$\mathbb{Z}$(Hom_R(C, I), $\mathbb{Q}$/$\mathbb{Z}$)是C-平坦R-模, φ是C-平坦预包络, 所以Hom_R(η, Hom_$\mathbb{Z}$(Hom_R(C, I), $\mathbb{Q}$/$\mathbb{Z}$))是正合的.这就说明了η是Hom_R(C, I)⊗-正合的.我们要说明K和M有同样的性质, 即S⊗_RK是$\mathscr{G}$_{$\tilde C$}-平坦S-模.考虑推出图

因为S是平坦R-模, 所以非零第一行正合.因为S⊗_RM是$\mathscr{G}$_{$\tilde C$}-平坦S-模, 所以非零第一列正合.使得$\tilde F$₀是平坦S-模, G是$\mathscr{G}$_{$\tilde C$}-平坦模.同时注意到

$\tilde F$₀根据文献[5]的命题3.1, S⊗_RF⁰是平坦S-模, 故C⊗_R S⊗_RF⁰是$\tilde C$-平坦S-模.

考虑短正合列0→$\tilde C$⊗_S$\tilde F$₀→X→S⊗_RK→0, 由引理4可知, 要证明S⊗_RK是$\mathscr{G}$_{$\tilde C$}-平坦的, 需说明：

(ⅰ) X是$\mathscr{G}$_{$\tilde C$}-平坦的；

(ⅱ) (S⊗_RK)⁺是$\mathscr{G}$_{$\tilde C$}-内射的.

对(ⅰ), 因为S是关于$\mathscr{G}$_{$\tilde C$}-平坦S-模扩张封闭的环, 所以X是$\mathscr{G}$_{$\tilde C$}-平坦的.下证(ⅱ), 将函子Hom_R(-, $\mathbb{Q}$/$\mathbb{Z}$)作用于上图非零第二行, 有

这里X⁺是$\mathscr{G}$_{$\tilde C$}-内射S-模, ($\tilde C$⊗_S$\tilde F$₀)⁺是$\tilde C$-内射S-模, 故($\tilde C$⊗_S$\tilde F$₀)⁺也是$\mathscr{G}$_{$\tilde C$}-内射S-模, 于是(S⊗_RK)⁺的$\mathscr{G}$_{$\tilde C$}-内射维数有限.从而要说明(S⊗_RK)⁺是$\mathscr{G}$_{$\tilde C$}-内射S-模, 根据文献[13]的命题2.12的对偶版只需说明对任意的$\tilde C$-内射S-模Hom_R($\tilde C$, $\tilde J$), 有

即可.而

故只需

根据引理5, 只需

用Hom_R(C, I)⊗-作用正合列

因为Tor_>0^R(Hom_R(C, I), M)=0, 并根据文献[6]的引理2.3, 有C⊗ F⁰┬Hom_R(C, I), 所以

从而(S⊗_RK)⁺是$\mathscr{G}$_{$\tilde C$}-内射的, 则S⊗_RK是$\mathscr{G}$_{$\tilde C$}-平坦S-模, 这就说明了K和M有同样的性质.