-
非线性共轭梯度法具有算法简便,存储量低的特点,是解决大规模问题的一种常用而且高效的方法之一,近来许多研究者将其推广到求解大规模非线性单调方程组问题,成为优化领域的一个研究热点[1-7].
本文考虑大规模非线性单调方程组
式中g:
$ {{\mathbb{R}}^{n}}\to {{\mathbb{R}}^{n}}$ 是连续可微的非线性函数;对∀x,y ∈$ {{\mathbb{R}}^{n}}$ ,有如下单调性质:令范数函数
$\theta(\mathit{\boldsymbol{x}}) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{g}}(\mathit{\boldsymbol{x}})} \right\|^2}$ ,其中‖·‖是欧氏范数,那么非线性单调方程组问题(1)等价于如下全局最优化问题:本文基于经典Liu-Storey共轭梯度法,在文献[8]的基础上,结合文献[1, 7, 9]的方法,设计一个新的搜索方向公式,利用文献[10]提出的超平面投影技术和文献[11]一类新型的线搜索,提出一种求解大规模非线性单调方程组的修正Liu-Storey投影算法.
全文HTML
-
本节扼要介绍共轭梯度法,然后设计一个新的搜索方向公式,结合超平面投影技术和某种线搜索方法,提出一个新Liu-Storey投影算法.
共轭梯度法迭代公式为
其中:xk+1是下一个迭代点,xk是当前迭代点;αk是步长,由某种线搜索确定;dk是搜索方向,迭代公式定义为
其中:βk是共轭调控参数,gk为g(xk)的简写.经典共轭梯度法有FR方法(Fletcher-Reeves)、PRP方法(Polak-Ribière-Polyak)、CD方法(Conjugate-Descent)和LS方法(Liu-Storey)等[12].
经典的LS方法和PRP方法在解决大规模无约束优化问题上,数值结果普遍较好,然而全局收敛性较差.而搜索方向的充分下降性和信赖域性质在共轭梯度法全局收敛性中起到关键的作用[1, 2, 12-17].
文献[14]提出一个修正的PRP公式,得到了较好的结果.其参数公式为
其中:常数
$ \mu > \frac{1}{4}$ ,yk+1=gk+1-gk.参数公式βkDPRP满足共轭条件和非负性.文献[8]在此基础上提出一个新的参数公式为
βkMPRP不仅满足共轭条件和非负性,而且还具有充分下降性,在Wolfe-Powell线搜索下算法全局收敛,数值试验结果表明算法有效.但βMPRP公式不具有信赖域性质.
文献[7]进一步提出修正公式
其中:常数
$\mu > \frac{1}{4} $ ,λ>0,γ>0.该公式具有信赖域性质,克服了文献[8]的不足.在适当的条件下证明了算法具有全局收敛性,数值结果表明方法能有效求解大规模非线性单调方程组.文献[8]还给出了具有充分下降性的修正βLS公式,指出在此公式上建立的算法在适当条件下具有全局收敛性的结论,并给出了该算法的初步数值试验分析,结果表明该算法比经典LS算法更优.但文献[8]没有给出算法的搜索方向充分下降性和全局收敛性的证明.其修正βLS公式定义为
其中:
$ {\beta ^{{\rm{LS}}}} = \frac{{\mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{y}}_{k - 1}}}}{{ - {\rm{ }}\mathit{\boldsymbol{g}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{d}}_{k - 1}}}},{\rm{ }}{\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{g}}_k} - {\mathit{\boldsymbol{g}}_{k - 1}}$ .该修正β公式也不具有信赖域性质.本文在文献[8]的基础上,结合文献[1, 7, 9]关于共轭参数的修正方法,设计一个新的搜索方向dk+1.此搜索方向不依赖任何线搜索,不仅具有充分下降性,还具有信赖域性质.新的搜索方向dk+1公式定义为
其中:
$ \mu > \frac{1}{4}$ ,λ>0,γ>0.为便于表述,本文将修正Liu-Storey投影算法称为MLS算法,其步骤如下:
步骤1:给定初始点x0∈
$ \mathbb{R}$ ,常数λ,γ,s>0;$ \mu > \frac{1}{4}$ ,ρ,ε∈(0,1),令k:=0;步骤2:若‖ F(xk)‖≤ε,则停止,否则转步骤3;
步骤3:通过式(8)计算搜索方向dk;
步骤4:利用式(9)计算步长αk
搜索步长αk=max{s,ρs,ρ2s,…},常数σ>0,s>0,ρ∈(0,1).
步骤5:利用公式计算下一个迭代点zk=xk+αkdk;
步骤6:若‖ F(zk)‖≤ε,则停止,并令xk+1=zk,否则,通过式(10)计算xk+1,
步骤7:令k:=k+1,转步骤2.
备注:式(9)为文献[11]提出的一种新的单调线搜索技术,适合应用于非线性单调方程组.步骤6运用了文献[10]提出的超平面投影技术,即xk+1是当前迭代点xk在超平面Hk={ x ∈
$ {{\mathbb{R}}^{n}}$ | g(zk)T(x -zk)=0}上的投影,其证明如下:
-
讨论MLS算法的全局收敛性,需要以下常规性假设H:
(H1) 非线性方程组(1)的解集非空,且水平集Ω={x∈
$ {{\mathbb{R}}^{n}}$ :g(x)≤g(x1)}有界.(H2) 函数g:
$ {{\mathbb{R}}^{n}}\to {{\mathbb{R}}^{n}}$ 是Lipschitz连续的,即∃L>0,使得由假设(H1)可知,存在常数ω>0,使得‖ x ‖≤ω,x*是问题(1)的解,即g(x*)=0,联合假设(H2)有
这说明存在一个常数
$\vartheta $ =2ωL>0,使得首先引入两个重要的引理.
引理2 [7] 如果假设H成立,序列{xk}由MLS算法生成,x*是非线性单调方程组(1)的解,那么有
和
成立.
联合超平面投影技术式(10)和线搜索技术式(9),得到
从共轭梯度法的迭代公式出发,通过引理2的式(16),容易得到下面结论:
接下来的引理3说明本文所选定的线搜索能够保证得到一个正数步长,使得MLS算法在有限步内停止,从而说明我们提出的MLS算法是有意义的.
引理3 若假设H成立,则MLS算法是适定的.
证 假设‖gk‖→0不成立,或者MLS算法不停止,那么∃η>0,使得
下面证明满足式(9)的步长αk存在下界.
假设存在k′使得式(9)不成立,那么对∀i∈
$ \mathbb{N}$ ∪{0},令αk′(i)=ρis,有由充分下降性式(11)和假设(H2)有
由信赖域性质式(12)和式(14)可得
联合式(12),(19)和(20),可得
这与αk′(i)的定义矛盾,从而说明线搜索(9)能够保证存在一个步长αk>0,使得MLS算法在有限步内终止.因此,引理3成立.
由以上的假设H、引理1、引理2和引理3,可证明下列MLS算法的全局收敛性.
定理1 如果假设H成立,序列{αk,dk,xk,gk}由MLS算法生成,则
证 反证法.假设式(21)不成立,则存在一个常数υ>0,使
由信赖域性质式(12),有
由引理2序列{xk}有界,则存在一个聚点
${\boldsymbol{\tilde{x}}} $ 和无限指标集N1,使得根据式(12)和式(14)得到
这说明序列{dk}有界,所以也存在一个聚点
$ {\boldsymbol{\tilde{d}}}$ 和无限指标集N2,使得联合式(17),可得
由线搜索技术式(9)可得,存在
$ {{{{\alpha }'}}_{\ k}}=\frac{{{\alpha }_{k}}}{\rho }$ ,使得当k→∞时,对∃k∈N2,(23)式两边取极限,即有
而式(11)两边同取极限,得到
显然产生矛盾.所以假设不成立,即式(21)成立.证毕.
-
为检验MLS算法的有效性,本节将对MLS算法与经典LS算法[12]、3项LS算法[12]求解大规模非线性单调方程组问题进行数值试验和比较分析.
选取具有固定初始点的10个经典非线性函数[18-19],具体的函数名称与初始点见表 1.
试验环境:Windows 7操作系统,Inel Pentium(
$ \mathbb{R}$ ) DuaCore CPU E5800 3.2 GHz,内存4 GB RAM,MATLA2014a.终止条件:‖ g(x)‖≤10-5或NI≥1 000.参数设置:μ=0.97,λ=0.01,γ=0.78,σ=0.11,ε=10-5,维数为[4 500,12 000,24 000,30 000,45 000]. 表 2给出了3种算法的试验结果,表中NI表示迭代次数,NF表示函数计算的次数,t表示程序运行所需要的时间.
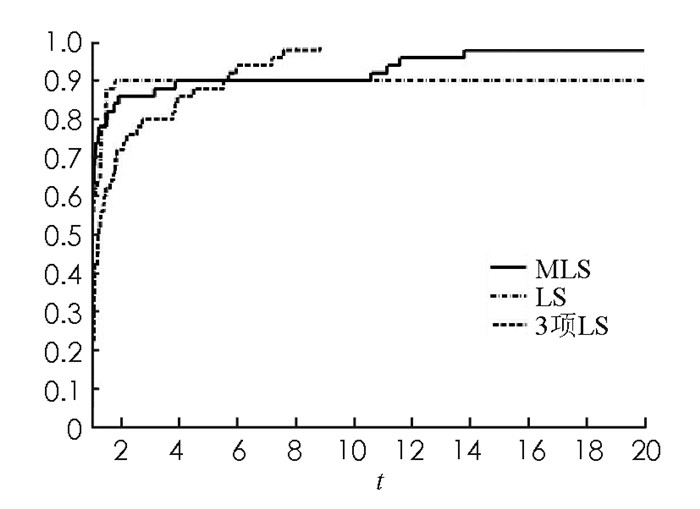
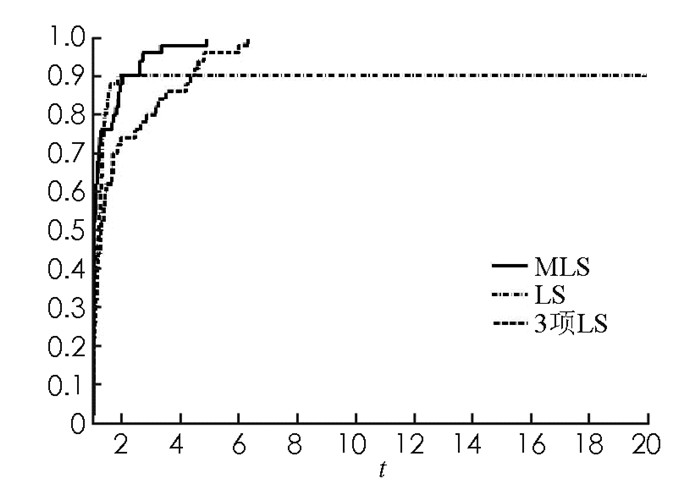
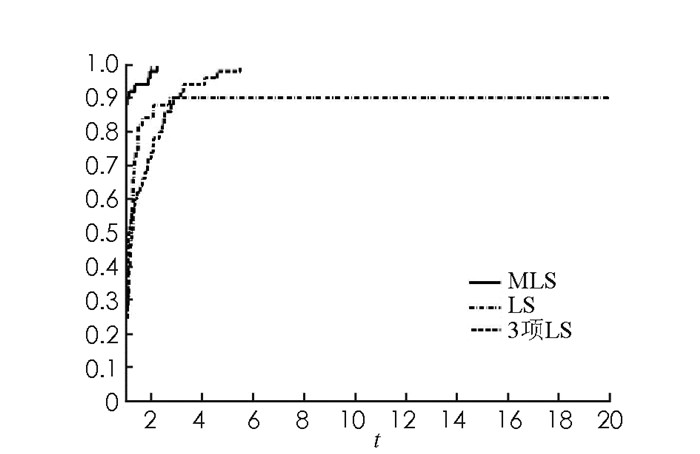
从表 2可以看出,在相同的条件精度下,MLS算法在迭代次数NI和CPU运行时间这两个测试指标上比经典LS算法和3项LS算法好;在目标函数值计算次数上,MLS算法与经典LS算法有微小差异,比3项LS算法更优.为更直观反映出MLS算法、LS算法和3项LS算法的性能,采用文献[20]提出的评价方法,分别给出这3种算法在迭代次数(NI)、目标函数值计算次数(NF)和运行时间等测试结果的性能比较图(图 1-图 3).这3个曲线图表明论文提出的MLS算法总体上比经典LS算法和3项LS算法更优,鲁棒性更好,适合用来求解大规模非线性单调方程组问题.



 下载:
下载: