高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

一种适用于配网暂态数据的高阶求导方法

,  ,  ,  , 

上一篇

下一篇

蒋文弢, 李世勉, 冯宗琮, 等. 一种适用于配网暂态数据的高阶求导方法[J]. 西南大学学报（自然科学版）, 2021, 43(12): 191-197. doi: 10.13718/j.cnki.xdzk.2021.12.022
引用本文: 蒋文弢, 李世勉, 冯宗琮, 等. 一种适用于配网暂态数据的高阶求导方法[J]. 西南大学学报（自然科学版）, 2021, 43(12): 191-197. doi: 10.13718/j.cnki.xdzk.2021.12.022
shu
JIANG Wentao, LI Shimian, FENG Zongcong, et al. A High-Order Derivation Method for Distribution Network Transient Data[J]. Journal of Southwest University Natural Science Edition, 2021, 43(12): 191-197. doi: 10.13718/j.cnki.xdzk.2021.12.022
Citation: JIANG Wentao, LI Shimian, FENG Zongcong, et al. A High-Order Derivation Method for Distribution Network Transient Data[J]. Journal of Southwest University Natural Science Edition, 2021, 43(12): 191-197. doi: 10.13718/j.cnki.xdzk.2021.12.022
shu

一种适用于配网暂态数据的高阶求导方法

  • 1.

    国网重庆市电力公司北碚供电分公司，重庆 400700

  • 2.

    重庆理工大学/重庆市能源互联网工程技术研究中心，重庆 400054

  • 基金项目: 国网重庆市电力公司2019年研究开发项目(2019渝电科技自51#)；国家自然科学基金项目(51607020)；重庆市教育委员会科学技术研究项目(KJQN201801113)
详细信息
    作者简介:

    蒋文弢，硕士研究生，工程师，主要从事电网控制、运维、检修等研究 .

    通讯作者: 陈勇，硕士研究生，工程师

  • 中图分类号: TP393

A High-Order Derivation Method for Distribution Network Transient Data

  • 1.

    Beibei Power Supply Branch of State Grid Chongqing Electric Power Company, Chongqing 400700, China

  • 2.

    Chongqing University of Technology/Chongqing Engineering Research Center of Energy Internet, Chongqing 400054, China

  • 摘要: 现在配网中的各类算法大都需要对数据进行高阶求导，传统高阶求导方法由于其自身理论的局限，在低阶和高阶情形下都难以准确计算. 为了提高计算精度，本文提出一种新的高阶求导方法，在多项式拟合法的基础上，通过分析配网中电压电流信号的暂态特性，合理选取拟合的基底函数，用最小二乘法计算基底函数系数以实现对目标函数的拟合，将新的拟合函数代替原离散数据作求导运算，在保证抗干扰能力的同时克服了传统多项式拟合法在高阶情形下的局限. 仿真结果表明，本方法在高阶和低阶情形下都有较高的准确性和良好的抗干扰能力.
    Abstract: Nowadays, all kinds of algorithms in distribution network need high-order derivation of data. Due to the limitation of their own theories, the traditional high-order derivation methods are difficult to calculate accurately in both low-order and high-order cases. In order to improve the calculation accuracy, a new high-order derivative method is proposed in this paper. Based on the polynomial fitting method, by analyzing the transient characteristics of voltage and current signals in the distribution network, the base function is selected for fitting reasonably, and the coefficient of the base function is calculated by the least square method to fit the objective function. The new fitting function is used to replace the original discrete data for derivative operation, which not only ensures the anti-interference ability, but also overcomes the limitations of the traditional polynomial fitting method in high-order cases. Simulation results show that this method has high accuracy in high-order and low-order cases, and has good accuracy and anti-interference ability.
  • 加载中

  • 图 1  配网暂态电流采样信号

    下载: 全尺寸图片 幻灯片

    图 2  无干扰情况下N=1，5，8，13，15时各方法效果比较

    下载: 全尺寸图片 幻灯片

    图 3  有干扰情况下N=1，3，5，8时各方法效果比较

    下载: 全尺寸图片 幻灯片
  • [1] 姜杰, 王鹏, 黄正炫, 等. 基于改进线路参数模型的配网电缆单相接地测距方法[J]. 电网技术, 2012, 36(5): 185-189. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201205034.htm
    [2] 张开迪. 分布参数电路模型及其在特高压线路保护中的应用研究[D]. 重庆: 重庆大学, 2014.
    [3] 李村晓. 电力系统综合负荷模型辨识策略研究及建模平台开发[D]. 长沙: 湖南大学, 2007.
    [4] 刘光晔, 汪洋, 彭丽, 等. 应用非线性等值原理解析计算电压稳定临界点[J]. 中国电机工程学报, 2013, 16: 129-136. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201316019.htm
    [5] 唐昆明, 杨伟, 张太勤, 等. 基于Stehfest算法的配网单相接地故障双端测距方法[J]. 电力系统保护与控制, 2015, 43(14): 76-83. doi: 10.7667/j.issn.1674-3415.2015.14.012
    [6] 康丽红, 唐昆明, 罗建, 等. 直流输电线路单极接地双端故障测距[J]. 电网技术, 2014, 38(8): 2268-2273. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201408039.htm
    [7] 康淑瑰, 岳亚卿, 郭建敏. 分数阶微分方程奇异系统边值问题正解的存在性[J]. 西南大学学报(自然科学版), 2019, 41(4): 104-108. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2019.04.015
    [8] 孙煜, 龙见仁, 覃智高, 等. 非线性复微分方程的解与Hω∞空间[J]. 西南大学学报(自然科学版), 2018, 40(10): 83-88. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2018.10.014
    [9] 康安明. 非线性系统多维泰勒网控制的稳定性分析及性能优化[D]. 南京: 东南大学, 2017.
    [10] doi: http://www.onacademic.com/detail/journal_1000040482021610_8cca.html CUI H R, WEI P B, MU Y P, et al. SARIMA-Orthogonal Polynomial Curve Fitting Model for Medium-Term Load Forecasting[J]. Discrete Dynamics in Nature and Society, 2016(7): 1-9.
    [11] TAN T T, CHEN W L, WANG D W, et al. Wind Power Prediction Based on Wind Farm Output Power Characteristics Using Polynomial Fitting[C] //2012 Asia-Pacific Power and Energy Engineering Conference. March 27-29, 2012, Shanghai, China. IEEE, 2012: 1-4.
    [12] 黄小军, 李雪妮. 涉及微分多项式和分担值的正规定则[J]. 西南大学学报(自然科学版), 2012, 34(10): 96-101. doi: http://xbgjxt.swu.edu.cn/article/id/jsunsz20121018
    [13] 计卫星, 张露露, 陈娟, 等. 一种时序数据多项式拟合加速方法[J]. 北京理工大学学报, 2018, 38(5): 519-524. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG201805013.htm
    [14] EICHINGER F, EFROS P, KARNOUSKOS S, et al. A Time-Series Compression Technique and Its Application to the Smart Grid[J]. The VLDB Journal, 2015, 24(2): 193-218. doi: 10.1007/s00778-014-0368-8
    [15] SIKORA R, MARKIEWICZ P, PABJANCZYK W. Multivariable Polynomial Fitting of Controlled Single-Phase Nonlinear Load of Input Current Total Harmonic Distortion[J]. Open Physics, 2018, 16(1): 137-142. doi: 10.1515/phys-2018-0021
    [16] 王伟, 焦彦军. 暂态信号特征分量在配网小电流接地选线中的应用[J]. 电网技术, 2008, 32(4): 96-100. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200804025.htm
    [17] 张长春, 王一夫, 刘钢, 等. 配电网故障暂态信号的逼近处理方法[J]. 重庆大学学报, 2018, 41(11): 53-58. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE201811006.htm
    [18] 李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008.
    [19] 谭伟杰, 冯西安, 张杨梅. 基于Hankel矩阵分解的互素阵列高分辨目标定向[J]. 西南大学学报(自然科学版), 2016, 38(7): 191-198. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2016.07.030
  • 加载中
图( 3)
计量
  • 文章访问数:  1804
  • HTML全文浏览数:  1804
  • PDF下载数:  141
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-07-08
  • 刊出日期:  2021-12-20

一种适用于配网暂态数据的高阶求导方法

    通讯作者: 陈勇，硕士研究生，工程师
    作者简介: 蒋文弢，硕士研究生，工程师，主要从事电网控制、运维、检修等研究
  • 1. 国网重庆市电力公司北碚供电分公司，重庆 400700
  • 2. 重庆理工大学/重庆市能源互联网工程技术研究中心，重庆 400054
  • 收稿日期:  2020-07-08
基金项目:  国网重庆市电力公司2019年研究开发项目(2019渝电科技自51#)；国家自然科学基金项目(51607020)；重庆市教育委员会科学技术研究项目(KJQN201801113)

摘要: 现在配网中的各类算法大都需要对数据进行高阶求导，传统高阶求导方法由于其自身理论的局限，在低阶和高阶情形下都难以准确计算. 为了提高计算精度，本文提出一种新的高阶求导方法，在多项式拟合法的基础上，通过分析配网中电压电流信号的暂态特性，合理选取拟合的基底函数，用最小二乘法计算基底函数系数以实现对目标函数的拟合，将新的拟合函数代替原离散数据作求导运算，在保证抗干扰能力的同时克服了传统多项式拟合法在高阶情形下的局限. 仿真结果表明，本方法在高阶和低阶情形下都有较高的准确性和良好的抗干扰能力.

English Abstract

    全文HTML

  • 开放科学（资源服务）标志码（OSID）：

  • 电力系统安全可靠的运行离不开其底层数据的支持，在电力系统相关数据的处理和计算中，高阶求导的计算随处可见，如时域下分布参数线路模型的推导和计算[1-2]、电力系统等值参数模型的建立[3]、电力系统负荷模型辨识研究[4]、故障测距[5-6]等. 高阶求导[7-8]已经渗透到电力系统的方方面面，它不仅和电网相关模型紧密相关，还与电力系统状态评估、故障处理、保护策略有着密切联系[9-11]. 由此可见，高阶导数的准确计算在电力系统中是十分重要的基础工作.

    电力系统中我们常处理的数据大都是电压电流信号的采样值，即离散数据，此时连续函数的求导公式不再适用，目前常用的方法有差分求导法和多项式拟合求导法. 差分求导法是利用导数的定义和微分的思想，近似求取某点处的导数，采样频率越大，其精度就越高，实现简单方便[12]. 但受边界效应的影响，采样区间首端或尾端的导数值不确定，即自由度减1，N点采样值只能确定N-1个一阶导数值，阶次每高一阶，自由度便少1，其根本原因是在对连续函数进行截断和采样处理时，必然会造成首尾信息缺失，而且不可避免，更关键的是差分法抗干扰能力极差，微弱的干扰便能造成很大的误差. 多项式拟合法[13-15]用一串线性无关的多项式(x，x2，…，xn)对离散数据进行拟合，将离散数据转化成连续函数，以连续函数逼近的方式代替求解，此方法受拟合精度的影响，若拟合精度低，则误差大. 此外，求导阶次受拟合多项式最高次数制约，n次多项式的n阶导数为常数，n-1阶导数为一元函数，以此类推，其求导阶次在接近多项式多高阶次后误差明显.

    针对上述弊端，本文提出一种正弦多项式拟合的方法求取电网离散数据的高阶导数值，本方法在多项式拟合的基础上，针对电力系统电压电流暂态分量和稳态分量的特征，合理选取正弦多项式函数为基底，具有良好的抗干扰性和可靠性.

1.   正弦多项式拟合原理

  • 电网下的电压电流暂态信号通常可表示成以下形式[16-17]，以电流信号为例：

    其中，i(t)，is(t)，it(t)分别表示电流信号、电流稳态分量、电流暂态分量，ω为工频下的角速度即100π，暂态分量it(t)由直流衰减分量和高频衰减分量g(t)组成，τ1为直流衰减分量的时间常数.

    正弦多项式拟合不同于一般多项式拟合所选取的基底x，x2，…，xn，为了使所选多项式更贴合配网数据，在分析上述配网数据所呈现的特征后，将多项式中加入正弦函数，又考虑到实际运行中暂态分量会衰减并归零，如图 1所示，因此在多项式中施加指数衰减函数以约束暂态分量，最终用正弦多项式p(t)拟合暂态信号的形式为

    其中：

    式(2)中，用带衰减的正弦多项式拟合暂态分量，其中，ω为工频下的角速度即100π，τ2为衰减时间常数，大小可根据实际电网数据进行调节和校正.

    于是问题变成求取p(t)中未知系数A0，B0，a0，b0，…，an，bn的值以逼近目标值i(t). 求取未知系数的值可用最小二乘法实现[18]：

    式(3)表示目标函数，误差平方和最小；式(4)中，下标i表示第i个采样序列，ti表示采样时间，p(ti)表示ti时刻的拟合值，i(ti)表示ti时刻的实际值，δi表示第i个采样值的拟合误差.

2.   算法实现

  • 将式(2)展开可得：

    其中：

    设共采样m+1个点，将式(5)中表示时间的变量t改写为离散采样时间ti(i=0，1，…，m)后，代入式(4)，则求误差平方和‖δ‖22最小值问题可转换成求多元函数

    的极值点O(a0*，a1*，…，a2n+3*). 令

    由此得：

    则式(7)可表示为

    为了方便用MATLAB实现，可将式(8)用矩阵表示[19].

    创建矩阵A，B，

    其中φi(tj)表示函数φi(t)在tj时刻的值.

    所以式(8)可表示为

    式(9)是关于正弦多项式系数aj的线性方程组，由于多项式φj(j=0，1，…，2n+3)线性无关，故方程组系数矩阵A>*A′满秩，有唯一解，记为点O(a0*，a1*，…，a2n+3*).

3.   仿真分析

  • 以直流衰减和高频衰减信号模拟电流信号对本方法进行验证，并将其和传统差分法和多项式拟合法进行对比.

    设故障后电流信号为

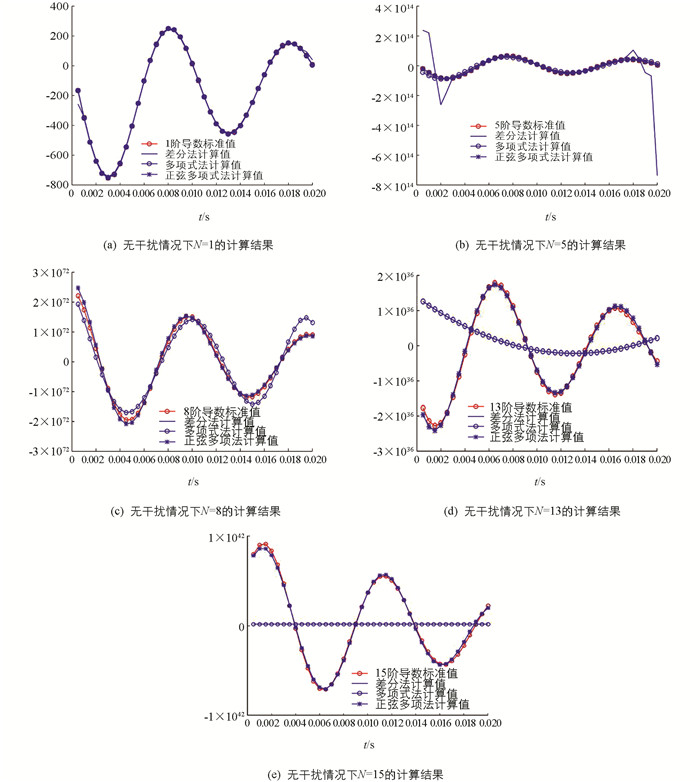
    取采样频率为2 000 Hz，采样周期为0.02 ms，正弦多项式最高次数n=15，τ2=0.02，在不加干扰情况下验证求导阶次N分别取1，5，8，13，15时的情况，如图 2所示.

    在图 2中，各阶导数标准值是根据电流信号表达式由导数计算公式计算而来，多项式拟合法计算的值是对拟合函数进行求导计算而来. 由图可知，差分法难以摆脱边界效应的影响，在低阶导数情况下首尾已经出现明显误差，在N=1时还可以忽略微小误差，但当N增大到5之后，其误差不容忽视且随着N增大，误差越发严重，所以，后面在计算更高阶导数时没有呈现差分求导的结果，但其数据中部效果显著；多项式法在求解低阶导数时具有较高的准确度，在N增大到8(大约n/2)时，依然有较高的准确度，随着N接近n，多项式拟合法误差越发明显，当N达到其多项式最高次数15时，计算结果为一个常数；正弦多项式拟合法在求解低阶导数时基本和实际值吻合，其误差肉眼难辨，即使阶次增高，其大部分区间依然保持超高吻合度，整体误差小. 不难看出，无论N取多少，正弦多项式精确度都远高于其他两种方法，低阶次情况下多项式法和正弦多项式法效果接近，阶次越高，正弦多项式的优势越明显.

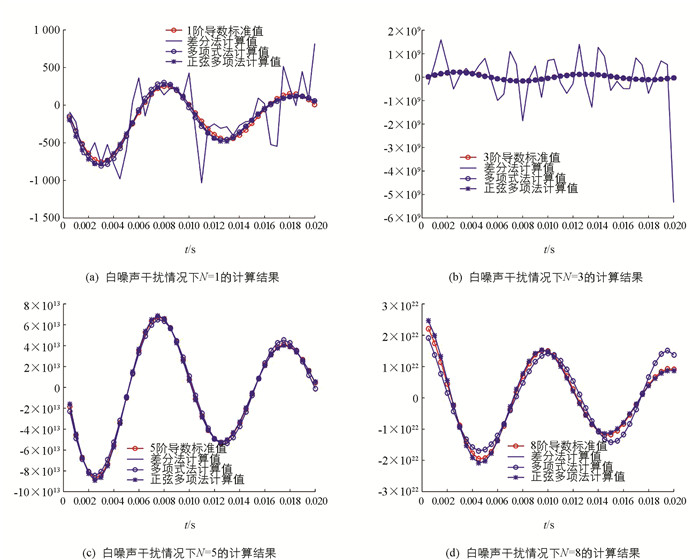
    在电流信号中加入微弱的白噪声，信噪比为20 dB，在加干扰后验证求导阶次N分别取1，3，5，8时的情况，如图 3所示.

    由图 3可知，即使加入的干扰信号十分微弱，在低阶次情形下，差分法依旧表现极大误差，它的抗干扰性能最差. N=3时差分法求导出来的结果和标准值背离太大，因此在后面计算更高阶导数时同样没有呈现差分求导的结果. 综合对比图 2和图 3，特别是从N=8的图像可知，在有干扰情况下，正弦多项式拟合法和多项式拟合法的计算结果和没干扰时几乎相同，都表现出优秀的抗干扰能力.

4.   结论

  • 传统高阶求导计算方法因其自身局限性无法保证计算准确性；差分法的边界效应对首尾区间的影响在高阶次时无法忽视和避免，也没有抗干扰能力，在微弱干扰环境下便不再适用；多项式拟合法在实际应用中多项式必然是有限项，无法避免求导阶次受限于多项式最高次数的问题，无法在高阶次情况下保证精度，给计算结果带来巨大的偏差，对要求计算快速可靠将造成十分严重的影响. 本文提出的正弦多项式拟合法在含直流衰减或高频衰减的情形下都具有优于传统方法的特性，一方面在大幅提高高阶次的精度的同时，在低阶次也可将误差控制得极小；另一方面由于算法中核心方程组具有唯一解，可使拟合函数的参数具有较强的稳定性，有利于表征相关物理特性，因而具有非常高的准确性和抗干扰能力.

参考文献 (19)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回