-
随着信息和互联网技术的飞速发展,媒体报道对人们日常生活的影响越来越重要,尤其在传染病防控方面,表现更为突出. 以2020年全球爆发的新型冠状病毒肺炎(COVID-19)为例,新闻媒体每日播报的实时疫情数据增长的趋势导致人们关注疫情的发展动态,并且积极主动配合政府推行的各项防控措施,包括减少出行、戴口罩、勤洗手、保持社交距离等,目的在于遏制病毒在人群中的进一步扩散和传播. 可见,媒体报道在疾病防控中有着举足轻重的作用. 近几年,已有不少学者借助动力学模型模拟了媒体报道对于传染病传播的影响[1-13]. 这些文献中的建模思路大致可以分为两大类,一类是将媒体报道模拟为状态变量如文献[4-8, 10];另一类则是通过修正传染系数来刻画媒体报道[1-3, 9, 11-14]. 对于后者,已有文献中采用的形式包括
$ \beta \mathrm{e}^{-a_1 E-a_2 I-a_3 H}, \beta \mathrm{e}^{-a I}, \left(\beta_1-\beta_2 \frac{I}{m}\right)+I $ 且m>0以及β1-β2f(I),其中E,I和H分别表示媒体报道的潜伏者、染病者和入院治疗的数量. 这些通过修正传染系数来刻画媒体报道的模型都是假设媒体报道对于传染系数的影响是即时的,也就是t时刻报道的感染人数会立刻改变人们的行为. 事实上,人们通过媒体报道获取到相关信息后,会经历一个判别过程,后续根据判别得到的结论再来做出相应的反应. 即t-τ(0≤τ < t)时刻报道的感染人数会影响疾病的传播. 因此在本文中,我们将考虑具有时滞效应的媒体报道对SIS传染病模型动力学性态的影响.
全文HTML
-
以流感背景,并基于经典的SIS传染病模型,将媒体报道的染病人数对疾病发生率的影响用函数e-αI(t-τ)来刻画,建立如下的模型:
其中:S(t)和I(t)分别表示t时刻的易感染者和染病者人数,Λ表示易感者的常数输入率,μ表示自然死亡率,γ表示染病者的恢复率.
-
在本节中,我们将先分析模型(1)的解的非负性和有界性,再借助极限系统理论给出平衡点的存在性.
对于任意τ>0,记:
$\bar{C}: =C\left([-\tau, 0], \mathbb{R}^2\right)$ 是区间[-τ,0]上的Banach空间,并定义模为$\bar{C}_{+}: = C\left([-\tau, 0], \mathbb{R}_{+}^2\right)$ . 令‖φ‖=sup-τ≤θ≤0|φ(θ)|初始值$\varphi(\theta)=\left(\varphi_1(\theta), \varphi_2(\theta)\right) \in \bar{C}_{+} \times \bar{C}_{+}, \varphi_i(\theta)>0$ ,i=1,2. 对于模型(1),先来说明对任意的非负初值S(0)=φ1(0)≥0,I(0)=φ2(0)≥0, t∈[-τ,0],有I(t)≥0,t≥0.事实上,由模型(1)中的第二个方程直接计算可得
显然,I(t)≥0,t∈(0,τ]. 进而,类似计算得
以上分析说明,对于任意非负初值,必有I(t)≥0,t≥0成立.
下面说明S(t)≥0,t≥0成立. 假设∃t1>0,使得S(t)>0,t∈(0, t1),S(t1)=0,且S(t)>0,t>t1. 则有
与S(t) < 0,t>t1矛盾. 也就是假设不成立. 即S(t)≥0,t≥0成立.
以上分析说明,模型(1)中任意具有非负初值的解一定是非负的. 下面来说明模型(1)解的有界性. 将模型(1)中的两个方程相加可得
由于
$\lim\limits _{t \rightarrow \infty}(S(t)+I(t))=\frac{\varLambda}{\mu}$ ,记$N_*=\frac{\varLambda}{\mu}$ ,这说明N*是方程(2)的全局渐近稳定的平衡点. 也就是,$\varOmega_1=\left\{(S, I): S \geqslant 0, I \geqslant 0, S+I \leqslant \frac{\varLambda}{\mu}\right\}$ 是模型(1)的正向不变集.另外,利用再生矩阵的办法[15]可以得到模型(1)的基本再生数为
将S(t)=N*-I(t)代入模型(1),可得模型(1)的极限模型
利用极限系统理论可知[16],模型(3)与模型(1)有相同的动力学性态. 接下来的研究将借助模型(3)来分析模型(1)的动力学性态.
为了分析方便,我们令
$X(t)=\frac{I(t)}{N_*}, a=\beta N_*, b=\alpha N_*, c=(\mu+\gamma)$ ,其中a,b,c>0. 则模型(3)可重新写为相应地,有
$R_0=\frac{a}{c}$ ,并且模型(4)的正向不变集为Ω2={X:0≤X≤1}. 下面将研究模型(4)的动力学性态.显然,模型(4)始终有零平衡点X0=0. 为了找到模型(4)的正平衡点X*,令
通过直接计算可得:f(0)=a,f(1)=0,且f′(X) < 0,这说明a>c时,也就是,当R0>1时,模型(4)存在唯一的正平衡点X*,满足a e-bX*(1-X*)=c. 即下面的定理成立:
定理1 模型(4)始终存在零平衡点X0=0,并且当R0>1时,模型(4)还存在唯一的正平衡点X*,满足a e-bX*(1-X*)=c.
事实上,模型(4)的零平衡点X0对应模型(1)的无病平衡点
$\boldsymbol{E}_0=\left(\frac{\varLambda}{\mu}, 0\right)$ . 而正平衡点X*对应模型(1)的地方病平衡点$\boldsymbol{E}_*=\left(\varLambda+\frac{\gamma I_*}{\mu+\beta \mathrm{e}^{-\alpha I *}}, I_*\right)$ ,I*=X*N*. 即,模型(1)始终有无病平衡点E0. 而当R0>1时,模型(1)还存在唯一的地方病平衡点E*.下面研究模型(4)的零平衡点和正平衡点的稳定性.
定理2 如果R0 < 1,模型(4)的零平衡点X0是全局渐近稳定的;如果R0>1,X0是不稳定的.
证 直接计算可得,模型(4)在X0=0处的特征方程为
即λ=c(R0-1). 由Hurwitz判据可知,若R0 < 1,有λ < 0,即模型(4)的零平衡点是局部渐近稳定的. 若R0>1,则λ>0,这说明模型(4)的零平衡点是不稳定的.
下面来证明零平衡点的全局稳定性. 记V1(t)=X(t),则
显然,当R0 < 1时,V′1|(4) < 0,故模型(4)的零平衡点是全局渐近稳定的. 证毕.
定理3 如果R0>1,τ=0,那么模型(4)的正平衡点X*是全局渐近稳定的.
证 直接计算可知,模型(4)在X=X*处的特征方程为
当τ=0时,特征方程(7)可重新写为
即特征值
$\lambda=-\frac{c X_*+b c X_*\left(1-X_*\right)}{1-X_*}$ . 由于X*∈(0,1),则λ < 0成立,进而,利用Huiwitz判据可得X*是局部渐近稳定的.为了证明正平衡点的全局稳定性,构造Lyapunov函数
$V_2(X)=X-X_*-X_* \ln \frac{X}{X_*}$ ,则由于y=e-bX是一个递减函数,因此,有(X-X*)(e-bX-e-bX*) < 0成立. 也就是,V′2|(4)≤0. 另外,当且仅当X=X*时,V′2|(4)=0. 这说明M={X|V′2(x)=0}={X*},也就是,模型(4)在M上的最大不变集就是{X*}. 根据LaSsalle不变集原理可知,当R0>1时,模型(4)的正平衡点X*是全局渐近稳定的. 证毕.
由定理2和定理3可知,当R0 < 1时,模型(1)的无病平衡点E0和地方病平衡点E*是全局渐近稳定的.
-
在本小节中将讨论τ>0时,模型(4)可能发生的Hopf分支. 为此,假设λ=iω,ω>0,代入方程(7)可得
进而有
也即
如果方程(12)有一个正根ω0,则正平衡点X*的稳定性可能会随着τ的改变而改变. 为此,记c*=e-bX*,则当b>1且c*>e1-b时,方程(12)存在一个正根
进而可得
其中
$\tau_k \in\left(\frac{\pi}{2}+2 k \pi, \pi+2 k \pi\right), k=0, 1, 2, \cdots \cdots$ 因此,
其中
$Q=\frac{c X_*}{1-X_*}$ . 进而由于
$\operatorname{sign}\left\{\left.\operatorname{Re}\left(\frac{\mathrm{d} \lambda}{\mathrm{d} \tau}\right)^{-1}\right|_{\lambda=i \omega_0}\right\}=\operatorname{sign}\left\{\left.\frac{\operatorname{Re}(\mathrm{d} \lambda)}{\mathrm{d} \tau}\right|_{\tau=\tau_k}\right\}$ . 可得$\operatorname{Re}\left(\frac{\mathrm{d} \lambda}{\mathrm{d} \tau}\right)>0$ .利用泛函微分方程的Hopf分支理论[17],得到下面的结论.
定理4 假设R0>1,
(1) 若0 < b≤1,则对任意τ≥0,模型(4)的正平衡点X*是渐近稳定的;
(2) 若b>1,c*≤e1-b,则对任意τ≥0,模型(4)的正平衡点X*是渐近稳定的;
(3) 若b>1,c*>e1-b,则对任意τ∈[0,τ0],模型(4)的正平衡点X*是渐近稳定的;
(4) 若b>1,c*>e1-b,则对任意τ≥τ0,正平衡点X*是渐近稳定的;且在τ=τk,k=0,1,2…时,模型(4)会在X*处发生Hopf分支.
-
在本小节中,将利用文献[18-19]中的全局Hopf分支理论来讨论模型(4)产生的局部Hopf分支的全局延拓问题. 为此,引入变换y(t)=x(τt),模型(4)可被改写为
这里yt(θ)=y(t+θ),θ∈[-1,0],yt∈X,X=C([-1,0],T),并且
引入下面的记号:
记
$C\left(y_t, \tau_k, \frac{2 \pi}{\omega_0 \tau_k}\right) \in \sum$ 是方程(17)的驻解$\left(y_*, \tau_k, \frac{2 \pi}{\omega_0 \tau_k}\right)$ 的联通分支,其中ω0和τk分别满足(13)式和(14)式.由文献[19]可知,如果方程(17)的驻解
$({ \mathop y\limits^ \wedge }, \tau, T) \in P$ 有形式为$\operatorname{i}m \frac{2 \pi}{T}\left(m \in \mathbb{N}_{+}\right)$ 的纯虚特征根,则称$({ \mathop y\limits^ \wedge }, \tau, T)$ 为中心. 进一步,如果$({ \mathop y\limits^ \wedge }, \tau, T)$ 是其领域内唯一的中心,并且只有有限个形式为$\operatorname{i}m \frac{2 \pi}{T}(m \in \left.\mathbb{N}_{+}\right)$ 的特征根,则称$({ \mathop y\limits^ \wedge }, \tau, T)$ 为孤立中心. 令$J({ \mathop y\limits^ \wedge }, \tau, T)$ 为使得$\operatorname{i}m \frac{2 \pi}{T}$ 是孤立中心$({ \mathop y\limits^ \wedge }, \tau, T)$ 的特征根的所有正整数m的集合.$m \in J({ \mathop y\limits^ \wedge }, \tau, T)$ 时,$\gamma_m({ \mathop y\limits^ \wedge }, \tau, T)$ 为中心$J({ \mathop y\limits^ \wedge }, \tau, T)$ 的第m个横截数,否则取$\gamma_m({ \mathop y\limits^ \wedge }, \tau, T)=0$ .引理1 方程(17)的所有周期解是一致有界的.
证 设y(t)是方程(17)的一个非平凡的周期解,且令y(t1)=N和y(t2)=n分别为其最大值和最小值,满足0 < n < N≤1,以及y′(t1)=y′(t2)=0,则代入(17)式可得
故N≠0,进而由方程(18)可得
$N=1-\frac{c}{a} \mathrm{e}^{b y(t-1)} < 1-\frac{c}{a}=1-\frac{1}{R_0}$ . 证毕.引理2 如果b>1,且c*>e1-b满足,方程(17)没有周期为1或2的周期解[19].
证 方程(17)的任意非平凡的周期为1周期解为u(t),且为如下常微分方程的非平凡周期解:
由于一阶纯量常微分方程不存在非平凡周期解,故(20)式不存在周期解.
若(17)式有周期为2的非平凡周期解u(t),则u1(t)=u(t),u2(t)=u(t-1),并且满足
由(21)式与y(t)相对应的周期轨道包含在如下区域:
则对所有的(u1,u2)∈G1总存在
其中u=min(u1,u2)且
$0 < \bar{n}=\frac{1}{2}\left(1-\frac{1}{R_0}\right) < N$ ,所以对所有的(u1,u2)∈G1有因此由Bendixson周期解不存在准则[20]知(21)式没有平凡周期解. 证毕.
引理3 如果
$1 < b < 4 \sqrt{2}\left(1-\frac{1}{R_0}\right)<N, c_*>\mathrm{e}^{1-b}$ 满足,那么方程(17)没有周期为4的周期解.证 设y(t)为方程(17)的周期为4的周期解,并令ui(t)=y(t-i+1),i=1,2,3,4. 于是u(t)=(u1(t),u2(t),u3(t),u4(t))是下述常微分方程的周期:
由引理1可知(22)式与y(t)相对应的周期轨道包含在如下区域:
解的一致有界性表明所有周期解均位于G2内,为了说明方程(17)没有4的周期解,只需证明方程(17)在区域G2中不存在周期解即可. 那么为证明方程(17)在区域G2中不存在周期解,我们将应用高维常微分方程Bendixson准则[20]得到方程(22)右端的Jacobi矩阵为
这里记Ai=c-a(1-2ui)e-bui+1,Bi=abui(1-ui)e-bui+1,u5=u1,i=1,2,3,4.
下面对
$\mathbb{R}^6$ 选取向量模:那么复合阵J[2](u)关于该范数的Lozinsk
${\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over i} }} $ 测度μ(J[2](u))为其中(i,j)∈{(1,4),(2,1),(3,2),(4,3)},(p,q)∈{(1,3),(2,4)}.
要使μ(J[2](u)) < 0,当且仅当对所有u∈G2,使得
这里u=min(ui,uj),
$f(u)=1-2 u+\frac{\sqrt{2}}{8} b$ . 根据文献[19]中的定理7.3.2,若对所有u∈G2有μ(J[2](u)) < 0,那么方程组(22)没有周期解. 由(25)式可知μ(J[2](u)) < 0当且仅当对所有u∈G2满足:接着证明(26)式. 显然f(u)是递减函数,在区域G2上
$f(u)-\frac{1}{R_0} \leqslant 0$ ,意味着$u \geqslant \frac{1}{2}\left(1-\frac{1}{R_0}\right)+\frac{\sqrt{2}}{16} b$ ,取$\tilde{n}=\frac{1}{2}\left(1-\frac{1}{R_0}\right)+\frac{\sqrt{2}}{16} b$ ,由(18)式可知$N < 1-\frac{1}{R_0}$ . 当$b < 4 \sqrt{2}\left(1-\frac{1}{R_0}\right), 0 < \tilde{n} < N$ 时,对所有$u \in (\tilde{n}, N)$ ,(25)式成立.综上所述,当
$1 < b < 4 \sqrt{2}\left(1-\frac{1}{R_0}\right), c_*>\mathrm{e}^{1-b}$ 时,有$-A_i-A_j+\sqrt{2} B_i < 0$ 成立.进一步有
其中
$u=\min \left(u_i, u_j\right), f(u)=1-2 u+\frac{\sqrt{2}}{8} b$ ,同理,对任意u∈G2有因此,应用文献[20]中的推论3.5可得方程组(22)不存在周期为4的周期解. 证毕.
定理5 1) 如果
$R_0>1, b>1$ ,且c*>e1-b,则对任意τ>τ1,方程(17)至少有一个非平凡的周期解.2) 如果
$R_0>1, 1 < b < 4 \sqrt{2}\left(1-\frac{1}{R_0}\right)$ ,且c*>e1-b,则对任意τ>τ0,方程(17)至少有一个非平凡的周期解.证 方程(17)是二次连续可微的,也就是文献[19]中的(A1)满足. 容易验证,
$D F\left(y_*, \tau_k, \frac{2 \pi}{\omega_0 \tau_k}\right)$ ,$\left(y_*, \tau_k, \frac{2 \pi}{\omega_0 \tau_k}\right) \in P$ ,即文献[19]中的(A2)满足. 方程(17)在驻解$({ \mathop y\limits^ \wedge }, \tau, T) \in P$ 处的特征方程为显然,F(y,τ,T)关于y可微,并且
$\varDelta_{({ \mathop y\limits^ \wedge }(\tau, T), \tau, T)}(\lambda)$ 关于(τ,T,λ)连续,这说明文献[19]中的(A3)满足. 那么对任意的$k=1, 2, 3 \cdots, \left(y_*, \tau_k, \frac{2 \pi}{\omega_0 \tau_k}\right) \in P$ 是孤立中心. 通过(15)式可知对每个k>0,存在εk,δk>0和一个光滑函数zk:(τk-δk,τk+δk)→C,使得对τ∈[τk-δk,τk+δk]成立,且
记
$T_k=\frac{2 \pi}{\tau_k \omega_0}$ ,且令显然,若|τ-τk|≤δk,并且对(u,T)≤∂Ωεk,有
$\operatorname{det} \varDelta_{(y *, \tau, T)}\left(z_k\left(u+\frac{\mathrm{i} 2 \pi}{T}\right)\right)=0$ ,则必有τ=τk,u=0,以及T=Tk. 这便证明了当m=1时,文献[19]中(A4)成立,进而可得到$J\left(y_*, \tau_k, \frac{2 \pi}{\omega_k \tau_k}\right)=\{1\}$ ,即文献[19]中(A5)成立. 另外有由文献[19]中的定理4.1.1可知,过
$\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 的连通分支$C\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 是非空的. 此外,有因此,由文献[19]中的定理4.1.2可知,过
$\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 的连通分支$C\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 是无界的.引理1说明连通分支
$C\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 在y空间上的投影是有界的. 当τ=0时,方程(17)为一阶纯量常微分方程,所以方程(17)没有非常数周期解. 进而可知,连通分支$C\left(y_*, \tau_k, \frac{2 \pi}{\tau_k \omega_0}\right)$ 在τ空间上的投影是有下界的. 利用τk和ω0的定义,即(13)和(14)式可得所以,
由引理3可知,当R0>1,
$1 < b < 4 \sqrt{2}\left(1-\frac{1}{R_0}\right)$ ,c*>e1-b成立时,如果(y,τ,T)∈$C\left(y_*, \tau_0, \frac{2 \pi}{\tau_0 \omega_0}\right)$ ,那么2 < T < 4. 所以连通分支$C\left(y_*, \tau_0, \frac{2 \pi}{\tau_0 \omega_0}\right)$ 在τ空间上的投影也是无界的. 又因在τ空间上的投影是有下界的,进而可得$C\left(y_*, \tau_0, \frac{2 \pi}{\tau_0 \omega_0}\right)$ 在τ空间上的投影包含区间[τ0,∞). (2)式成立. 类似地,由引理2可知,当k≥1时,$C\left(y_*, \tau_0, \frac{2 \pi}{\tau_0 \omega_0}\right)$ 在τ空间上的投影至少包含区间[τk,∞). (1)式成立. 证毕.
3.1. 全局Hopf分支的存在性
-
在本小节中,将借助数值模拟来验证所得理论结果的合理性. 为此,令a=1.2,c=0.3. 下面分情况讨论.
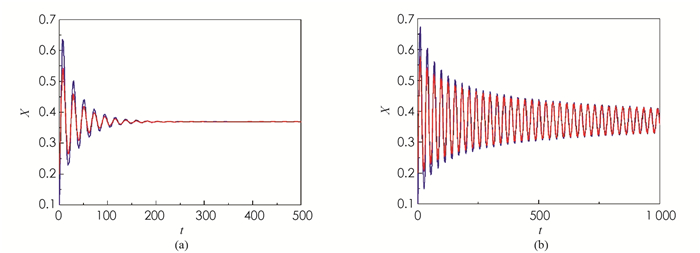
当b=0.8 < 1,τ=10时,如图 1(a)所示,模型(4)从不同初值出发的解最终都趋近于正平衡点X*,这说明X*是稳定的. 当b=1.5>1时,直接计算得e1-b=0.606 5>c*. 令τ=15,则X*仍是稳定的,见图 1(b).
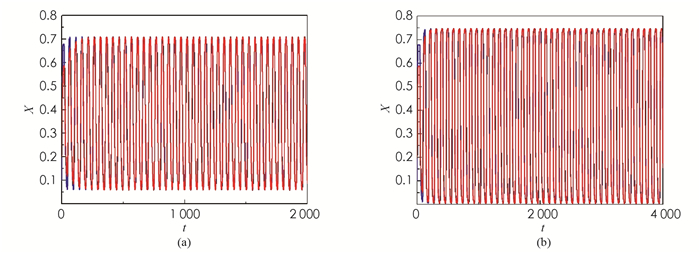
当b=2.5>1时,e1-b=0.223 1 < c*. 取τ=8 < τ0,图 2(a)表明模型(4)的平衡点X*仍保持稳定. 而一旦τ=10>τ0时,X*不再稳定,Hopf分支发生,见图 2(b).
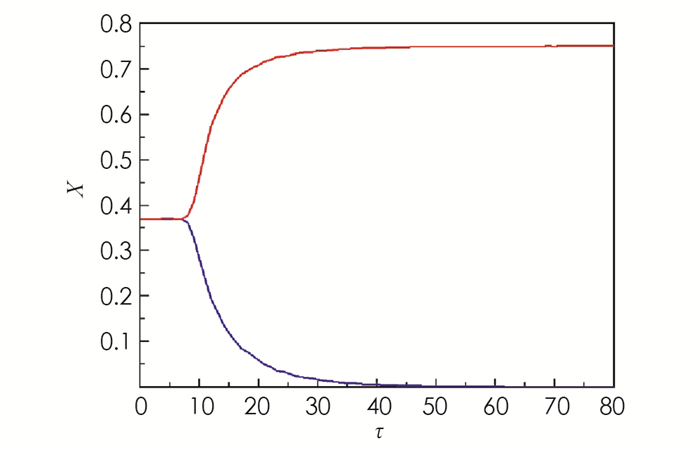
下面展示平衡点X*处的Hopf分支的全局延拓性. 此时令a=1.2,b=2.5,c=0.3,相应地,平衡点X*=0.369 8,R0=4>1,c*=0.396 7. 通过(13)和(14)式计算得τ0=8.517 9,τ1=37.833 8. 当b=2.5,并且分别满足定理5的条件1)和2)时,各自选取τ=40>τ1,τ=20>τ0,如图 3(a),(b)所示,两张图都展示了在平衡点X*附近从τ0分支出的周期解是大范围存在的.
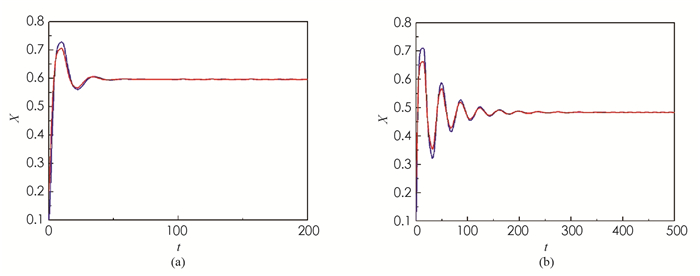
相应地,随着时滞τ的不断增加,模型(4)在平衡点X*处展现出了Hopf分支(图 4).
-
在本小节中,主要研究了媒体报道的染病者数量对SIS模型动力学性态的影响. 给出了模型(1)的基本再生数,借助极限系统,讨论了系统(4)平衡点的存在性、稳定性,以及平衡点不稳定时可能发生的Hopf分支. 当R0 < 1时,模型(1)存在全局渐近稳定的无病平衡点;而当R0>1时,模型(1)存在唯一的地方病平衡点,并且地方病平衡点的稳定性会随着时滞τ的增加而发生改变,即:在τ=0的情况下,地方病平衡点是全局渐近稳定的;当τ>τ0时,地方病平衡点不再稳定,并会发生全局延拓的Hopf分支. 我们也给出了发生全局Hopf分支延拓的条件.
系统(4)中的参数b=αN*,通过改变b的参数值大小,可以明显看出b值对平衡点的影响. 也就是说,由媒体报道的染病者数量所引起的时滞效应会使得模型的动力学性态更加丰富. 即媒体报道引起的时滞效应会改变地方病平衡点的稳定性,产生全局Hopf分支.



 下载:
下载: