高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

自适应边缘样本识别的深度聚类算法

,  ,  , 

上一篇

下一篇

李俊霞, 钱宇华, 马国帅, 等. 自适应边缘样本识别的深度聚类算法[J]. 西南大学学报（自然科学版）, 2023, 45(3): 34-46. doi: 10.13718/j.cnki.xdzk.2023.03.003
引用本文: 李俊霞, 钱宇华, 马国帅, 等. 自适应边缘样本识别的深度聚类算法[J]. 西南大学学报（自然科学版）, 2023, 45(3): 34-46. doi: 10.13718/j.cnki.xdzk.2023.03.003
shu
LI Junxia, QIAN Yuhua, MA Guoshuai, et al. Depth Clustering Algorithm for Adaptive Edge Samples Recognition[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 34-46. doi: 10.13718/j.cnki.xdzk.2023.03.003
Citation: LI Junxia, QIAN Yuhua, MA Guoshuai, et al. Depth Clustering Algorithm for Adaptive Edge Samples Recognition[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 34-46. doi: 10.13718/j.cnki.xdzk.2023.03.003
shu

自适应边缘样本识别的深度聚类算法

  • 1.

    山西大学 大数据科学与产业研究院，太原 030006

  • 2.

    山西大学 计算机与信息技术学院，太原 030006

  • 3.

    山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006

  • 基金项目: 国家重点研发计划项目(2021ZD0112400)；国家自然科学基金项目(62136005, 62106132)；山西省青年三晋学者项目；山西省高等学校科技创新项目(2019L0034)；山西省青年科学基金项目(20210302124556)
详细信息
    作者简介:

    李俊霞，硕士研究生，主要从事图神经网络及数据挖掘研究 .

    通讯作者: 钱宇华，教授，博士研究生导师; 

  • 中图分类号: TP391

Depth Clustering Algorithm for Adaptive Edge Samples Recognition

  • 1.

    Institute of Big Data Science and Industry, Shanxi University, Taiyuan 030006, China

  • 2.

    School of Computer and Information Technology, Shanxi University, Taiyuan 030006, China

  • 3.

    Key Laboratory of Computational Intelligence and Chinese Information Processing, Ministry of Education, Shanxi University, Taiyuan 030006, China

  • 摘要: 深度神经网络因其强大的非线性映射和特征提取能力被广泛应用于聚类中，然而，现有的大多数深度聚类网络仅仅考虑了样本的特征信息，并未有效利用样本空间位置的分布以及样本间的关联信息. 本研究融合了样本的特征信息以及样本间的空间位置信息和关联关系，提出了自适应边缘样本识别的深度聚类算法(Auto-CB). 在使用自编码器学习样本特征表示的同时，通过图神经网络学习样本间的结构信息；然后利用自注意力机制自适应地将样本划分为簇中心样本和边缘样本，并分别使用K-means和多数投票机制对其聚类；在5个数据集上与7个深度聚类以及基于图神经网络的聚类算法进行了性能对比. 结果表明，利用簇中心样本与边缘样本之间的潜在关联关系可以有效促进样本的特征表示，并在聚类任务中取得了更好的效果.
    Abstract: Deep neural network is widely used in clustering because of its powerful nonlinear mapping and feature extraction ability. However, most of the existing deep clustering networks only take the characteristic information of samples into account, and do not take full advantages of the spatial location distributions of samples and the correlation information between samples. This paper combines the characteristic information of samples, the spatial location information and correlation relationships between samples, and proposes an depth clustering algorithm, Auto-CB for adaptive edge sample recognition. While using the self-encoder to learn the feature representation of samples, the structural information between samples is learned through graph neural network. Then, the self-attention is used to adaptively divide the samples into cluster center samples and edge samples, K-means and majority voting mechanism are used to cluster them, respectively. This paper compares the performance of five data sets with seven deep clustering and clustering algorithms based on graph neural network. The results show that using the potential correlation between cluster center samples and edge samples can promote the feature representation of samples and achieve better results in clustering tasks.
  • 加载中

  • 图 1  自适应边缘样本识别的深度聚类算法模型

    下载: 全尺寸图片 幻灯片

    图 2  不同k值的聚类结果

    下载: 全尺寸图片 幻灯片

    图 3  簇中心样本和边缘样本比例的实验结果

    下载: 全尺寸图片 幻灯片

    图 4  预测结果与真实结果的可视化聚类效果

    下载: 全尺寸图片 幻灯片

    表 1  数据集基本情况

    数据集 类型 数量 种类 维度
    USPS Image 9298 10 256
    HHAR Record 10 299 6 561
    Reuters Text 10 000 4 2 000
    MINIST Image 10 000 10 784
    Fashion_MINIST Image 10 000 10 784
    下载: 导出CSV

    表 2  在5个数据集上的聚类结果(均值)

    Dataset Metric K-means AE DEC IDEC GAE VGAE SDCN Auto-CB
    USPS ACC 66.82 71.04 73.31 76.22 63.10 56.19 78.08 78.99
    NMI 62.63 67.53 70.58 75.56 60.69 51.08 79.51 77.97
    ARI 54.55 58.83 63.70 67.86 50.30 40.96 71.84 71.10
    F1 64.78 69.74 71.82 74.63 61.84 53.63 76.98 76.40
    HHAR ACC 59.98 68.69 69.39 71.05 62.33 71.30 84.26 86.36
    NMI 58.86 71.42 72.91 74.19 55.06 62.95 79.90 80.25
    ARI 46.09 60.36 61.25 62.83 42.63 51.47 72.84 73.11
    F1 58.33 66.36 67.29 68.63 62.64 71.55 82.58 83.32
    Reuters ACC 54.04 74.90 73.58 75.43 54.40 60.85 77.15 81.03
    NMI 41.54 49.69 47.50 50.28 25.92 25.51 50.82 60.31
    ARI 27.95 49.55 48.44 51.26 19.61 26.18 55.36 62.59
    F1 41.28 60.96 64.25 63.21 43.53 57.14 65.48 67.96
    MINIST ACC 52.15 65.11 57.96 66.84 64.59 56.53 81.63 82.35
    NMI 48.21 55.79 49.19 62.06 14.61 15.04 82.44 83.66
    ARI 36.397 43.63 36.42 50.38 37.27 33.58 75.92 76.86
    F1 52.50 60.25 55.44 59.91 15.92 14.86 79.49 80.23
    Fashion-MINIST ACC 46.69 58.15 54.04 66.84 58.91 55.42 53.68 55.86
    NMI 50.63 60.88 52.58 62.06 21.28 14.50 57.50 58.59
    ARI 33.92 45.24 37.62 50.38 44.67 30.26 40.41 56.76
    F1 44.28 55.95 52.47 59.91 18.56 13.37 52.81 54.16
    下载: 导出CSV

    表 3  损失消融的ACC指标

    数据集 AE None_CB Auto-CB
    USPS 71.04 77.23 78.99
    HHAR 59.98 76.11 86.36
    Reuters 54.04 80.10 81.03
    MINIST 52.15 81.50 82.35
    Fashion_MINIST 46.69 51.83 55.86
    下载: 导出CSV
  • [1] HINTON G E, SALAKHUTDINOV RR. Reducing the Dimensionality of Data with Neural Networks[J]. Science, 2006, 313(5786): 504-507. doi: 10.1126/science.1127647
    [2] VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and Composing Robust Features with Denoising Autoencoders[C] //ICML '08: Proceedings of the 25th international conference on Machine learning. 2008: 1096-1103.
    [3] SU S R, GAO Z F, ZHANG H Y, et al. Detection of Lumen and Media-Adventitia Borders in IVUS Images Using Sparse Auto-Encoder Neural Network[C] //2017 IEEE 14th International Symposium on Biomedical Imaging. Melbourne, VIC, Australia. IEEE, 2017: 1120-1124.
    [4] HAN J W, ZHANG D W, HU X T, et al. Background Prior-Based Salient Object Detection via Deep Reconstruction Residual[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(8): 1309-1321. doi: 10.1109/TCSVT.2014.2381471
    [5] XIE J Y, GIRSHICK R, FARHADI A. Unsupervised Deep Embedding for Clustering Analysis[C] //Proceedings of the 33rd International Conference on International Conference on Machine Learning-Volume 48. June 19-24, 2016, New York, NY, USA. New York: ACM, 2016: 478-487.
    [6] KING W I. The Annals of Mathematical Statistics[J]. The Annals of Mathematical Statistics, 1930, 1(1): 1-2. doi: 10.1214/aoms/1177733256
    [7] GUO X F, GAO L, LIU X W, et al. Improved Deep Embedded Clustering with Local Structure Preservation[C] //Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. August 19-26, 2017. Melbourne, Australia. California: International Joint Conferences on Artificial Intelligence Organization, 2017: 1753-1759.
    [8] JIANG Z X, ZHENG Y, TAN H C, et al. Variational Deep Embedding: an Unsupervised and Generative Approach to Clustering[C]//Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. August 19-26, 2017. Melbourne, Australia. California: International Joint Conferences on Artificial Intelligence Organization, 2017.
    [9] WANG C, PAN S R, HU R Q, et al. Attributed Graph Clustering: a Deep Attentional Embedding Approach[C] //Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. August 10-16, 2019. Macao, China. California: International Joint Conferences on Artificial Intelligence Organization, 2019.
    [10] PAN S R, HU R Q, FUNG S F, et al. Learning Graph Embedding with Adversarial Training Methods[J]. IEEE Transactions on Cybernetics, 2020, 50(6): 2475-2487. doi: 10.1109/TCYB.2019.2932096
    [11] BO D Y, WANG X, SHI C, et al. Structural Deep Clustering Network[C] //Proceedings of The Web Conference 2020. April 20-24, 2020, Taipei, New York: ACM, 2020: 1400-1410.
    [12] KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[EB/OL]. (2016-12-22)[2022-02-21]. https://arxiv.org/abs/1609.02907.
    [13] XIA C Y, HSU W, LEE M L, et al. BORDER: Efficient Computation of Boundary Points[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(3): 289-303. doi: 10.1109/TKDE.2006.38
    [14] QIU B Z, YUE F, SHEN J Y. BRIM: An Efficient Boundary Points Detecting Algorithm[M] //Advances in Knowledge Discovery and Data Mining. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007: 761-768.
    [15] 薛丽香, 邱保志. 基于变异系数的边界点检测算法[J]. 模式识别与人工智能, 2009, 22(5): 799-802. doi: 10.3969/j.issn.1003-6059.2009.05.020
    [16] 邱保志, 杨洋, 杜效伟. BRINK: 基于局部质变因子的聚类边界检测算法[J]. 郑州大学学报(工学版), 2012, 33(3): 117-120. doi: 10.3969/j.issn.1671-6833.2012.03.030
    [17] XIANG L L. Clustering Boundary Detection Technology for Mixed Attribute Data Set[J]. Control and Decision, 2015, 30(1): 171-175.
    [18] LORE K G. LLNet: a Deep Autoencoder Approach to Natural Low-Light Image Enhancement[J]. Pattern Recognition, 2017, 61: 650-662. doi: 10.1016/j.patcog.2016.06.008
    [19] DAI J J, SONG H, SHENG G H, et al. Cleaning Method for Status Monitoring Data of Power Equipment Based on Stacked Denoising Autoencoders[J]. IEEE Access, 2017, 5: 22863-22870. doi: 10.1109/ACCESS.2017.2740968
    [20] SUN M, ZHANG X W, VAN HAMME H, et al. Unseen Noise Estimation Using Separable Deep Auto Encoder for Speech Enhancement[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016, 24(1): 93-104. doi: 10.1109/TASLP.2015.2498101
    [21] ZENG K, YU J, WANG R X, et al. Coupled Deep Autoencoder for Single Image Super-Resolution[J]. IEEE Transactions on Cybernetics, 2017, 47(1): 27-37. doi: 10.1109/TCYB.2015.2501373
    [22] MEHTA J. RODEO: Robust DE-AliasingautoencOder for Real-Time Medical Image Reconstruction[J]. Pattern Recognition, 2017, 63: 499-510. doi: 10.1016/j.patcog.2016.09.022
    [23] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning Representations by Back-Propagating Errors[J]. Nature, 1986, 323(6088): 533-536. doi: 10.1038/323533a0
    [24] NG A. Sparse Autoencoder[J]. CS294A Lecture Notes, 2011(72): 1-19.
    [25] MAKHZANI A, FREY B. K-Sparse Autoencoders[EB/OL]. (2014-03-22)[2022-03-21]. https://arxiv.org/abs/1312.5663.
    [26] KIPF T N, WELLING M. Variational Graph Auto-Encoders[EB/OL]. (2016-11-21)[2022-03-21]. https://arxiv.org/abs/1611.07308.
    [27] VAN D, MAATEN L, HINTON G. Visualizing Data Using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(11): 2579-2605.
    [28] LE CUN Y, MATAN O, BOSER B, et al. Handwritten Zip Code Recognition with Multilayer Networks[C] //[1990] Proceedings. 10th International Conference on Pattern Recognition. June 16-21, 1990, Atlantic City, NJ, USA. IEEE, 2002: 35-40.
    [29] STISEN A, BLUNCK H, BHATTACHARYA S, et al. Smart Devices are Different: Assessing and MitigatingMobile Sensing Heterogeneities for Activity Recognition[C] //SenSys '15: Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems. 2015: 127-140.
    [30] LEWIS D D, YANG Y M, ROSE T G, et al. RCV1: a New Benchmark Collection for Text Categorization Research[J]. Journal of Machine Learning Research, 2004, 5: 361-397.
    [31] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-Based Learning Applied to Document Recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. doi: 10.1109/5.726791
    [32] XIAO H, RASUL K, VOLLGRAF R. Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms[EB/OL]. (2017-08-25)[2022-030-1]. https://arxiv.org/abs/1708.07747.
    [33] HARTIGAN J A, WONG M A. Algorithm AS 136: a K-Means Clustering Algorithm[J]. Applied Statistics, 1979, 28(1): 100. doi: 10.2307/2346830
  • 加载中
图( 4) 表( 3)
计量
  • 文章访问数:  1403
  • HTML全文浏览数:  1403
  • PDF下载数:  343
  • 施引文献:  0
出版历程
  • 收稿日期:  2022-08-10
  • 刊出日期:  2023-03-20

自适应边缘样本识别的深度聚类算法

    通讯作者: 钱宇华，教授，博士研究生导师; 
    作者简介: 李俊霞，硕士研究生，主要从事图神经网络及数据挖掘研究
  • 1. 山西大学 大数据科学与产业研究院，太原 030006
  • 2. 山西大学 计算机与信息技术学院，太原 030006
  • 3. 山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006
  • 收稿日期:  2022-08-10
基金项目:  国家重点研发计划项目(2021ZD0112400)；国家自然科学基金项目(62136005, 62106132)；山西省青年三晋学者项目；山西省高等学校科技创新项目(2019L0034)；山西省青年科学基金项目(20210302124556)

摘要: 深度神经网络因其强大的非线性映射和特征提取能力被广泛应用于聚类中，然而，现有的大多数深度聚类网络仅仅考虑了样本的特征信息，并未有效利用样本空间位置的分布以及样本间的关联信息. 本研究融合了样本的特征信息以及样本间的空间位置信息和关联关系，提出了自适应边缘样本识别的深度聚类算法(Auto-CB). 在使用自编码器学习样本特征表示的同时，通过图神经网络学习样本间的结构信息；然后利用自注意力机制自适应地将样本划分为簇中心样本和边缘样本，并分别使用K-means和多数投票机制对其聚类；在5个数据集上与7个深度聚类以及基于图神经网络的聚类算法进行了性能对比. 结果表明，利用簇中心样本与边缘样本之间的潜在关联关系可以有效促进样本的特征表示，并在聚类任务中取得了更好的效果.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID):

  • 聚类分析是通过挖掘物理或抽象对象的潜在关联关系，并依据某一特定标准将其划分为不同团簇的过程. 随着数据的爆炸式增长，依赖于计算样本距离的传统聚类算法对于高维、海量数据难以有效提取样本的特征从而达到理想的聚类效果. 具有非线性映射能力的深度神经网络，能够将高维的大规模数据特征映射到低维空间中，从而为聚类分析提供更好的数据. 由于自编码器泛化性强、无需标注的特点，自编码器[1]被用来将输入的高维数据压缩成高效的低维数据表示，从而进行下游任务，并在图像降噪[2]、目标识别[3-4]等方面取得了良好的效果.

    然而在对输入数据进行表示的过程中，自编码器通常仅仅关注于样本的自身特征，未考虑样本之间的潜在联系对样本特征学习和聚类分析的影响. 样本之间的结构信息可以有效地促进样本特征的判别性并且简化样本之间的复杂性，最典型的方法是图神经网络，通过捕捉样本之间的图结构信息，将邻域样本特征和自身特征进行融合，作为该样本的特征表示，使得样本的特征更适合聚类. 样本和样本之间往往存在着各种各样的深层次关联关系，虽然图神经网络能学习到样本的结构信息，但是往往需要很长的时间才能拟合出样本之间的分布. 因此通过只依靠神经网络学习样本之间的结构信息和特征信息远远不够，只有显式地利用样本和样本之间的结构关系，分析样本之间的空间位置分布，才能挖掘到样本之间的深层次信息，并且提高特征的判别能力.

    一般地，具有聚类性质的数据集在各个类簇之间往往存在着所属类别不明确的边缘样本. 类簇的密度通常由内到外越来越稀疏，簇中心样本密度相对密集，边缘样本相对稀疏. 边缘样本一般处于密度发生跳变的区域，同时具有两个或者两个类簇以上的特征，造成边缘样本在很大程度上与聚类内部的簇中心样本有着不同的性质. 边界区域的样本以及相应的邻域样本的隶属信息间接影响类簇的结构变化，因此，在聚类样本处理中，同一类簇中不同空间位置的样本应该进行区分度量.

    本研究针对现有的深度聚类算法中存在基于原始的K近邻算法构建样本之间的拓扑信息不足、易出现样本之间特征趋同、未考虑样本的空间分布以及样本之间的可分性较差等问题，提出了一种自适应边缘样本识别的深度聚类算法(Auto-CB)，将样本动态划分为边缘样本和簇中心样本来学习样本和样本之间的关联关系，显式利用样本与样本之间的关联关系促进聚类效果. 将5个数据集和7个深度聚类的算法进行了对比，结果表明Auto-CB算法能有效挖掘样本之间的关联关系并改善聚类效果.

1.   相关研究

  • 深度聚类分析是机器学习和数据挖掘领域中非常重要的一项技术，用于在大量复杂的数据中寻找数据之间隐含的分布模式以及关联性规则. 样本的特征表示学习决定聚类的效果，深度神经网络能对高维复杂数据分布进行模拟，具有强大的非线性拟合数据的表示能力. 2016年Xie等[5]提出深度嵌入聚类(DEC)模型联合优化深度嵌入特征表示和聚类，通过软分配进行迭代优化. 只使用深度自编码器中的编码器进行特征学习和优化，丢弃了解码器，通过计算辅助目标分布和最小化KL散度[6]之间的差异进行迭代，取得了良好的效果，成为了新的深度聚类算法的参考. 但是，DEC仅仅依靠聚类损失对编码器进行约束，破坏了数据结构以及扭曲了嵌入空间，削弱了嵌入特征的表示能力. 为此，Guo等[7]提出改进的深度嵌入聚类(IDEC)，保留了数据的局部结构，在聚类损失的基础上添加了重构损失，以约束自编码器学习更好的特征表示.

    尽管基于提取数据表示的深度神经网络取得了快速的进展，但是大多数模型未能有效提取样本之间隐藏的结构信息. 为了尽可能地捕捉不同数据样本之间的结构信息，一些研究工作开始在聚类中引入了图卷积神经网络. 2017年Jiang等[8]提出了基于自动编码器的图自编码器(GAE)和基于变分自编码器的变分图自编码器(VGAE). 2019年，Wang等[9]提出基于自注意力机制的图嵌入聚类网络(DAE)，在DEC聚类损失优化网络学习特征表示的基础上利用注意力机制学习样本之间的拓扑结构和特征表示. 2020年，Pan等[10]在GAE的基础上提出了一种图嵌入的对抗性正则化框架(ARGA，ARVGA). Bo等[11]提出将图结构信息集成到深度聚类中，并设计了双重自监督机制指导GCN[12]学习样本的多重数据结构和自编码器的多重数据表示相结合的结构化深度聚类网络(SDCN). 尽管经典的基于结构信息的聚类算法能获得较好的聚类效果，但是由于数据密度分布不均，类和类之间的边缘样本仍然难以区分.

    截止目前，已经提出了一系列的边缘样本检测方法. BORDER[13]算法根据数据样本的反向k近邻个数来检测边界样本，边界样本的反向k近邻的个数往往比簇中心样本的个数更少，但是在含有噪声的数据集中，BORDER算法并不能正确识别边缘样本和噪声样本. BRIM[14]算法利用数据点的正向和负向半邻域的样本个数的差别标注边界样本，算法能有效区分噪声样本和边缘样本，但是BRIM却不能检测多密度数据集的边缘样本. BAND算法提出了K距离的概念，并根据K距离定义提出局部密度和变异系数区分边缘样本，能有效区分噪声样本和边缘样本并且在多密度数据中依然能取得好的聚类效果[15]. BRINK算法在K距离的基础上提出了局部质变因子LOF的概念，根据LOF值的大小检测边界样本[16]. BERGE算法通过计算样本的局部密度的相关系数标记边缘样本，但是不能应用于高维空间[17].

    样本的空间分布以及样本之间复杂的关联关系在各个领域呈现出不同程度的需求. 在传统聚类任务中认为样本是互相独立的，通过计算样本之间的相似度对数据样本划分类簇，然而样本之间往往存在着各种各样不同强度的相关性甚至相互依赖关系. 虽然基于样本特征和数据结构进行聚类一定程度上获得了好的聚类效果，但是也存在一些不足：一是目前深度神经网络是把网络所有的节点看作同等重要，对节点之间的空间分布没有深入考虑和研究，不能合理地反映出不同样本在聚类中的影响程度. 二是没有显式地利用样本和样本之间的关联关系，只是依靠深度神经网络学习样本的特征和样本之间的结构信息，往往需要很长时间才能拟合出样本之间的非线性关系. 三是深层次的图神经网络容易产生过平滑现象，样本之间的可分性较差，对样本特征学习和图结构的信息利用不够充分.

    为了充分利用样本与样本之间的关联关系，本研究提出了基于自注意力的自适应样本划分深度聚类算法，在自编码器和图神经网络分别学习样本特征和结构信息的基础上，动态将样本划分为簇中心样本和边缘样本，通过显式挖掘和利用簇中心样本和边缘样本之间的关联关系，促进特征的学习和样本聚类.

2.   模型介绍

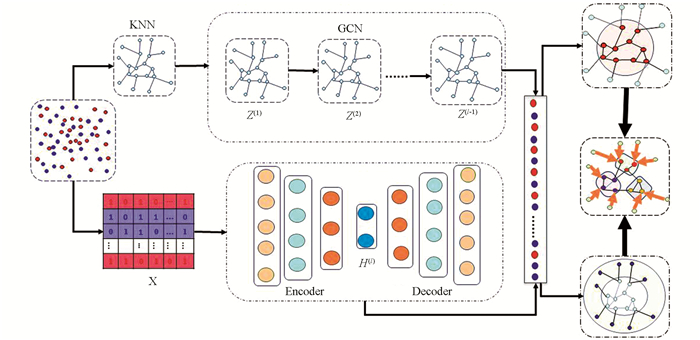
  • 本研究提出自适应的深度聚类算法，模型如图 1所示，包括3个部分：样本表示学习、样本结构信息、簇中心样本和边缘样本划分(Atuo-CB). 本研究由自编码器重构学习样本的特征表示，由GCN学习样本之间潜在的结构信息，提升样本的表征能力. 最后，本研究还根据样本所处的空间位置的不同将样本划分为边缘样本和簇中心样本，挖掘并利用边缘样本和簇中心样本的关联关系，从而促进网络的学习和聚类的效果. 本节将分别详细介绍自适应边缘样本识别的深度聚类算法的具体内容.

    • 2.1.   基本概念和术语

  • 给定一个无向图G=(V，E，A)，其中V代表n个样本的节点集合，E代表任意两个样本之间相似性矩阵. X(n×d)表示为n个样本的特征矩阵，其中xi表示为第i个样本，d表示为样本的维度. XT为X矩阵的转置矩阵，I是对角线为1的单位对角矩阵. A代表n×n的邻接矩阵，$\widetilde{A} $表示加入自循环的邻接矩阵. 使用KNN方法构建样本之间的相似性关系并形成邻接矩阵A.

    假设将含有n个数据样本的数据集X划分为c个类簇，即C={C1，C2，⋯，Cc}，Ci≠$ \varnothing$，i=1，2，⋯c. 则簇中心样本定义为：

    边界样本定义为：

    其中u，v∈X，Nu为样本u的邻居样本.

    • 2.2.   样本表示学习

  • 学习有效的表示是深度聚类的前提. 自编码器是一种通过无监督学习高效表示的前馈非循环神经网络，要求输入和学习目标相同，先将输入特征压缩成嵌入空间表示，然后通过这种表示来重构输出，具有非常强的提取数据表示的能力. 自编码器经常被用于数据增强[18-20]、图像重构[21-22]以及目标检测[3-4]等多种任务中，自编码器主要有传统自编码器[23]、降噪自编码器[2]、稀疏自编码器[24-25]以及变分自编码器[26]等. 本研究使用传统的自编码器，如图 1模型图的左下部分所示，自编码器部分由两个级联网络组成，第一个是编码器，第二个是解码器：

    其中$X \in R^{(n \times d)}$指的是输人编码器的原始数据的特征矩阵, $\hat{X}=H^{(l)}, \hat{X} \in R^{(n \times d)}$指的是解码器输出的特征矩阵. $x_i$指原始数据的第$i$个样本的特征, $h_i^{(l)}$是第$l$层编码器输出的中间特征向量的第$i$个样本的特征, $x^{\prime}{ }_i$指解码器第$i$个样本的输出特征, $f$和$g$为映射函数, $\|\cdot\|_F$为$F$-范数.

    • 2.3.   样本结构信息

  • 数据样本之间的关系揭示了样本之间潜在的相似性. 尽管传统的深度聚类方法在欧式空间数据提取特征方面取得了不错的进展，但是深度聚类在学习表示时却只关注数据本身的特征，深层特征缺乏针对性的鉴别能力，未考虑样本之间的关联结构信息. 图卷积神经网络(GCN)能够对样本的高阶邻域的结构信息进行融合，利用样本之间的拓扑信息能有效提高深层特征的判别能力，更好地反应样本之间的相关性. 通过图神经网络对不同样本赋予不同的权重系数，使得聚类更有针对性. 利用注意力对经过自编码器学习到的特征排序，从而划分出容易划分的簇中心样本和类别相对模糊的边缘样本. 如模型图 1的左上部分所示，本研究使用图神经网络学习样本的结构信息，图卷积神经网络GCN从第l-1层到第l层的特征学习信息传递过程为：

    其中$Z^{(l)}$表示图神经网络第$l$层的特征, $Z^{(l-1)}$为图神经网络的第$l-1$层特征, $Z^{(0)}$为自编码器的编码器输出的特征矩阵$X . \widetilde{D}_{i i}=\sum\limits_j \widetilde{A}_{i j}, W^{(l-1)}$为第$l-1$层的权重向量, $\varphi($.$) 为激活函数. 为了使深层特征同时$具有表示能力和结构信息, 本研究将图神经网络的结构信息和编码器的特征信息进行了融合, 将$G C N$第$l$-1层特征和编码器第$l$层的输出特征进行了拼接, 以获得蕴含多种信息的特征表示:

    为了使聚类目标能够促进深度聚类特征的学习，本研究使用软分配KL散度损失联合优化特征学习和聚类，KL散度是两个概率分布P和Q差别的非对称性度量函数. 其中P分布表示数据的真实分布，Q表示数据的理论分布：

    对于数据的理论分布，本研究使用Student-t分布[27]计算第i个样本和第j个质心的相似度：

    其中ui指的是第i个样本的特征，μj是K-means初始化获得的第j个质心. α是Student-t分布自由度，本研究设置α=1. qij是第i个样本划分到第j簇的软分配概率. 为了使编码器和图神经网络学习的数据特征表示不发散，更加靠近质心，KL散度通过利用P分布限制优化模型的表示，P分布为：

    • 2.4.   簇中心样本和边缘样本划分(Auto-CB)

  • 样本所处的空间位置与各个簇质心的距离是区分样本隶属的直接性测量工具，不同空间位置样本应赋予不同的加权系数. 与质心距离更近的簇中心样本与该类簇的关系更紧密，隶属度越大应该赋予更大的权重. 位于类簇交叉边界的边缘样本与质心越远，争议性越大，对整体样本的划分影响越大，加权系数应该偏小. 如图 1模型图的右半部分所示，本研究使用GCN来计算自注意力分数给处于不同空间位置的样本赋予不同的权重分数. 通过GCN利用样本特征和样本之间的拓扑结构学习到的注意力分数可以将样本划分为簇中心样本和边缘样本，其中S∈R(n×1)为每个样本获得的权重分数：

    根据GCN学习到的权重分数，选取前top-h个节点作为簇中心样本，h∈(0，1]是超参数决定簇中心样本的个数，为了统一，h设置为0.9. Cidx为簇中心样本对应的权重分数，Bidx为边界样本对应的权重分数.

    特征矩阵根据获得的注意力分数做掩码操作获得簇中心样本的特征矩阵和边缘样本的特征矩阵，U∈R(n×2d)为GCN第l-1层的输出和编码器第l层输出拼接的特征矩阵：

    邻接矩阵根据注意力分数做掩码操作获得簇中心样本和边缘样本之间关联关系的邻接矩阵：

    通过图卷积神经网络学习样本之间的结构特征，能准确地根据样本的空间分布，将样本划分为簇中心样本和边缘样本. 为了拉近簇中心样本和质心的距离，Auto-CB算法用余弦距离测量簇中心样本与质心的距离. 其中xi∈U(n×2d)为第i个簇中心样本，μj为第j个质心：

    边缘样本是距离质心较远的样本，边缘样本通过与簇中心样本建立关联关系从而与质心关联，并获得所属类簇. 为了防止一个孤立的样本与一个较远的簇中心样本建立关系，造成错误的聚类结果，本研究使用多数投票机制获得边缘样本的类簇. 每个边缘样本最终通过与┌vn┐个簇中心样本建立关系，并统计取类簇数最大的为最终该样本的类簇，其中v∈(0，1)为超参数，每个边缘样本最终由┌vn┐个样本决定一个边缘样本的类簇. 边缘样本和簇中心样本之间的损失为：

    综上所述，最终Auto-CB算法的总损失为：

3.   结果与分析

  • 为了测试提出的自适应边缘样本识别的深度聚类算法(Auto-CB)的性能，本研究在一些真实数据集上测试了模型的性能，并和一些最先进的算法进行了比较，详细数据情况展示在表 1. 使用4个常用的深度聚类的评价指标包括准确率ACC(Accuracy)、标准互信息NMI(Normalized Mutual Information)、兰德系数ARI(Adjusted Rand Index)和F1分数.

    • 3.1.   数据集描述

  • USPS[28]：美国邮政服务手写数字识别库. 库中含有9 298张手写数字图像，图片均为手写数字“0”至“9”的16×16像素的灰度图像，数据集中所有灰度值都已归一化.

    HHAR[29]：人类活动识别异质数据集. 以智能手机和智能手表传感器采集的传感器数据，当用户带着智能手表和智能手机按照特定顺序执行活动时，传感器会记录下用户的骑车、坐、站、走以及上下楼梯活动. 数据集一共包括10 299条记录.

    Reuters[30]：路透社数据集. 它是含有一系列短新闻以及对应主题的多类、多标签数据集，含有1万条数据，是简单并广泛使用的小型文本分类数据集.

    MINIST[31]：手写数字识别数据集. 机器学习领域中经典的一个数据集，每个样本都是“0”到“9”的一张28 ×28像素的灰度手写数字图片，共有10万个样本，本研究对数据集进行了处理，对每个类随机抽样10张图，最终采用1万个样本做模型的学习样本.

    Fashion-MINIST[32]：包含T恤、裤子、运动鞋、裙子、外套、凉鞋、汗衫、包包、裸靴、套衫10种类别的不同时尚穿戴品的图像，整体数据结构和Minist数据集完全一致，每张图片同样是28×28像素的灰度图片. 本数据集包含10万张图片，对每个类别随机抽样1 000张.

    • 3.2.   算法对比分析

  • K-means[33]：经典的传统聚类方法.

    AE[1]：基于编码器和解码器提取特征的深度神经网络，提取特征之后用K-means聚类.

    DEC[5]：在编码器基础上添加了聚类损失，通过聚类损失优化编码器提取的特征.

    IDEC[7]：在DEC的基础上添加了解码器的重构损失，提高了深度学习特征的能力.

    GAE&VGAE[8]：通过使用无监督的图自编码器和变分图自编码器提取样本特征.

    SDCN[11]：在自编码器学习特征的基础上融入了图的结构信息，利用GCN促进样本特征的提取.

    • 3.3.   实现细节

  • 为了方便比较和统一，本研究使用相同的网络模型参数，自编码器和解码器的维度是d-500-500-2000-10，GCN的维度是10-512-10-1. 提前预训练所有基于自编码器提取特征的模型迭代了30次，并且学习率都是0.001. 为了统一，设置核心点的比例是0.9，边界点的比例是0.1. 所有的数据集都迭代了200次. 为了便于比较，本研究直接引用了(SDCN)实验部分的数据结果，对于所有的数据集重复训练了10次，并且取了10次所有结果的平均值.

    • 3.4.   参数敏感性

    3.4.1.   K值影响分析

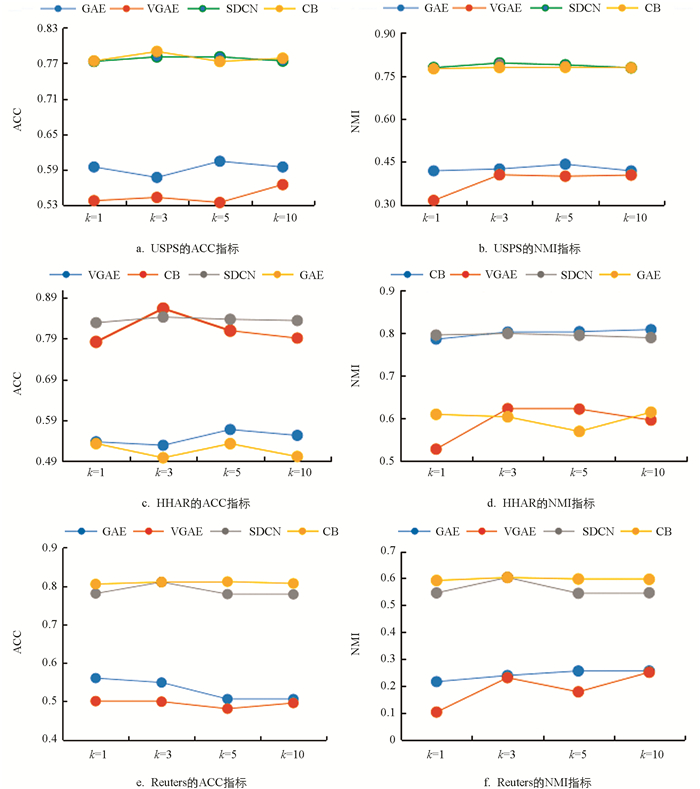
  • KNN构图，选择一个合理精准的k是KNN模型的必要条件. k值如果太小，样本之间的联系图会非常稀疏，模型不能很好泛化. k值如果太大，会出现联系图非常稠密，模型过于泛化，出现欠拟合. 图 2展示了部分数据集KNN建图时k为1，3，5，10时的ACC指标以及NMI指标的变化程度，但是从实验结果可以看出，随着k值的变化，Auto-CB算法几乎为一条直线，说明k值的变化并不影响Auto-CB模型的泛化能力和最终的聚类效果.

    • 3.4.2.   V值影响分析

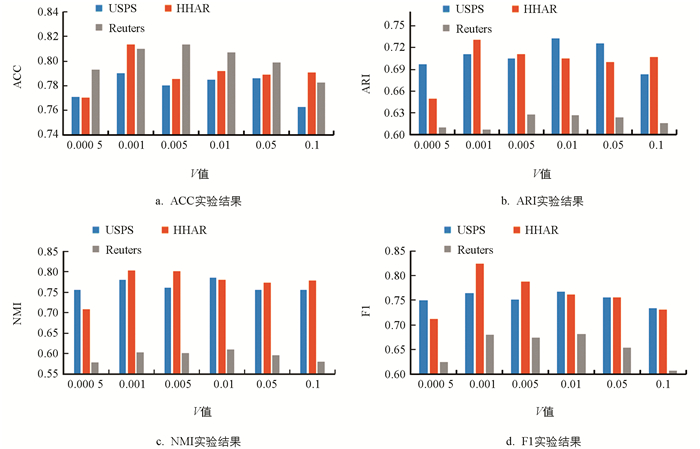
  • 虽然簇中心样本和边缘样本之间建立了关联关系，但并不是所有的边缘样本都和该类簇的簇中心样本建立直接关系. 仍然存在部分边缘样本处于类簇交叉区域，当v取值不同时边缘样本所在类簇的隶属程度可能较大，因此本研究使用多数投票机制判断边缘样本的类别. 图 3展示了部分数据集在不同v值的4个聚类指标结果，通过图 3可以看出每个边缘样本和核心样本的联系比例v的大小不同，最终的聚类效果会有所差别. 在v=0.001或者0.005时性能最好，但在v=0.000 5或者v=0.1时聚类效果会下降，这是因为v偏小时，会出现一个孤立的边缘样本与小部分的簇中心样本建立联系，容易出现误差. v偏大容易出现一个边缘样本与多个其他类簇偏远的样本建立联系，最终由多个决定，簇种类越多，距离越远，边缘样本的学习效果越差.

    • 3.5.   实验结果和分析

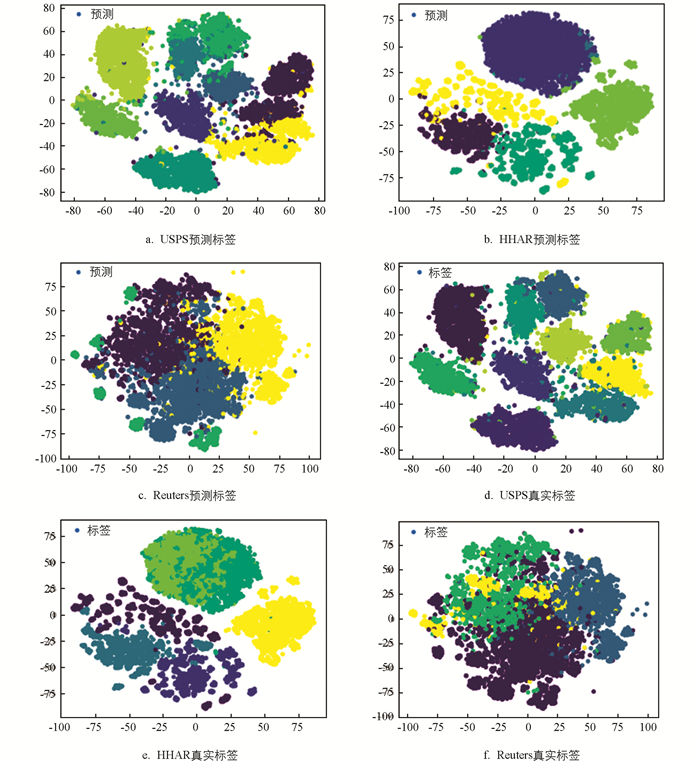
  • 本研究分别在5个数据集上将所提出的分离簇中心样本和边界样本的算法与7个经典的聚类模型对比方法进行了实验，实验结果和比较方法展示在表 2中，每行加粗值表示在该数据集上的最优值. USPS数据集、HHAR数据集、Reuters数据集的预测结果和真实标签的可视化聚类结果展示在图 4. 基于过程观察，可以得到以下的结论：

    1) 在HHAR数据集上，本研究提出的算法比第二好的SDCN算法分别在ACC，NMI，ARI，F1上提高了2.1%，0.35%，0.27%，0.74%；在Reuters数据集上，本算法比SDCN在ACC，NMI，ARI，F1提高了3.98%，9.49%，7.23%，2.48%；在MINIST数据集上，文中提出的算法平均提高了0.72%，1.22%，1.94%，0.74%. 该结果说明挖掘和分析样本与样本之间的关联关系能有效促进样本特征的提取和结构信息的利用，最终促进聚类的结果.

    2) 基于自编码器的深度聚类方法(AE，DEC，IDEC)明显优于原始的K-means方法和基于图卷积神经网络的方法(GAE，VGAE)，说明聚类的前提是学习有效的数据表示，要将聚类的目标融入到深度聚类强大的表征能力中可以使聚类效果更佳.

    3) 将图卷积神经网络和自编码器联合优化聚类目标和学习特征的SDCN明显优于单独的深度聚类方法，原因是SDCN融入了结构化信息，通过利用样本之间的结构信息来促进样本特征的学习. 但是SDCN在多个数据集上只是达到了次优的效果，这是因为SDCN忽略了样本和样本之间的关联关系，只依赖图神经网络隐式学习样本之间的结构关系，没有充分利用样本在网络中的空间结构信息，Auto-CB除了通过图神经网络隐式学习样本的结构信息，还通过显式将样本划分为边缘样本和簇中心样本，利用样本之间的关联关系，在HHAR，Reuters和MINIST数据集的4个指标上达到了最优效果.

    4) 在Fashion-MINIST数据集上模型整体表现不佳，原因一是Fashion-MINIST数据集整体特征比其他数据集的数据特征更为复杂，自编码器提取复杂特征的能力有限，不能通过自编码器充分提取数据特征，造成数据特征非常相似，簇中心样本和边缘样本不易划分. 二是KNN根据原始的数据特征进行建图，样本与样本之间的结构信息不够明显，基于GCN学习样本的图结构信息性能会有所下降. 综上所述，可以使用更加优异的图片特征提取器来改善该模型在此数据集上的聚类效果.

    5) 表 3展示了只有自动编码器的聚类，未根据样本的空间分布对样本分开处理，只考虑样本结构信息的聚类，以及考虑样本之间结构关系并根据样本的空间分布将样本划分为边缘样本和簇中心样本，进行分开处理，进而对比聚类之间ACC的指标. 通过实验发现，在自编码器和样本之间结构信息的基础上将样本划分为簇中心样本和边缘样本，考虑处于类簇交叉区域的边缘样本对于聚类整体结构影响的Auto-CB算法取得了相对较好的聚类结果，从而验证了Auto-CB算法的可行性. 在利用样本结构信息和特征信息的基础上引入了边界样本，并考虑其对于类簇划分的影响，本研究较好地分析了簇中心样本和边缘样本的差异性.

4.   结论

  • 本研究在自编码器学习样本表示和图卷积神经网络学习样本结构特征的基础上，基于样本的空间分布自适应将样本分为簇中心样本和边缘样本. 通过利用簇中心样本和边缘样本之间的关联关系促进样本特征的表示学习和样本结构信息收集，提出了基于自适应边缘样本识别的深度聚类算法(Auto-CB). 在各种开放的数据集上，Auto-CB算法获得了较好的聚类结果. 本研究通过KNN一次构建样本之间的结构信息，根据样本所处空间位置的不同赋予样本不同的权重，迭代式地将样本划分为边缘样本和簇中心样本，这种划分从侧面反映了样本之间的关系，可以获得更为详细地明确样本空间分布，更准确地获得边界样本的所属类别. 在接下来的任务中，将考虑根据任务多次迭代优化构建图结构信息，并对样本的局部信息和全局信息进行融合，通过样本的相似性动态捕获样本间的全局图结构信息.

参考文献 (33)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回