对于如下对流扩散模型方程

文献[2]中给出了形如

的四阶指数型紧致差分格式，系数为

此处δ_xu_i和δ_x²u_i分别定义为

该格式对于求解对流占优等大梯度变化的对流扩散问题具有高精度、高分辨率的优点.本文将基于该格式构造对流扩散反应方程的四阶指数型组合紧致差分格式.

本文考虑如下对流扩散反应方程

其中：ε为扩散项系数且ε>0，μ为对流项系数；b(x)和f(x)是关于x的足够光滑的函数；u(x)是待求未知量；当b(x)=0时，模型方程(6)即为文献[2]中的对流扩散方程.

首先将求解区间[X₁，X₂]等分为N个子区间：x_i=X₁+ih，i=0，1，2，…，N，$h=\frac{X_2-X_1}{N}$.

在点x_i处由泰勒级数展开得到

由(7)式得

再由(8)式和(9)式可得待求量的二阶导数u_xxi的四阶组合差分逼近公式

下面对对流扩散反应模型方程(6)的四阶指数型组合紧致差分格式进行推导.将模型方程(6)改写为如下形式

对(11)式中的第一个方程考虑其在点x_i处形如(2)式的四阶指数型紧致差分格式

其中α，c₁，c₂由(3)式给出.

对(11)式中的第二个方程两端的x求导得

将(13)式代入(12)式中，整理得

由(10)式得

并将其代入(14)式右端，略去高阶项整理得

下面通过对(15)式右端项中待求量的二阶导数采用不同的处理方法，得到以下求解模型方程(6)的两种四阶指数型组合紧致差分格式.

将(10)式代入(15)式中，消去u_xx项整理得

即得本文格式1：

其中

假设ε≠0时，将原模型方程(6)改写为

将其代入(15)式右端项，消去u_xx项整理得

即得本文格式2：

其中

若使(16)式和(18)式逼近模型方程(6)的精度达到四阶，则需要对F_i中的u_xi，f_xi采用四阶差分逼近.此处采用如下四阶Padé型紧致差分公式进行离散

其中U代表u或f.离散u_xi和f_xi，边界条件采用如下四阶逼近公式^[20]

令$\tilde{u}=\mathrm{e}^{\mathrm{i} k x}$，i为虚数单位，则

且由(20)式得

又令ω=kh，$P e=\frac{|\mu|}{\varepsilon} h$， $Count =\left|\frac{b}{\mu}\right| h$，$\eta=P e \cdot Count =\frac{|b|}{\varepsilon} h^2$，则微分方程(6)精确的特征函数为

经过计算可得文献中的FOC格式^[14]、文献[18]格式、MHOC格式^[19]、本文格式1和本文格式2的特征函数均可统一地表示为如下形式

其中相应的M₁和M₂的表达式详见表 1.

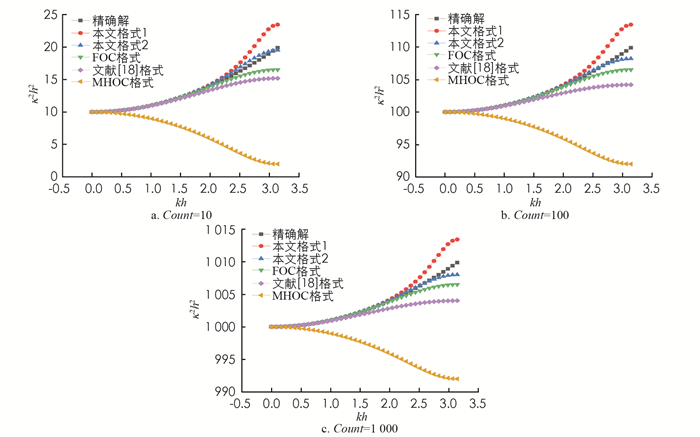
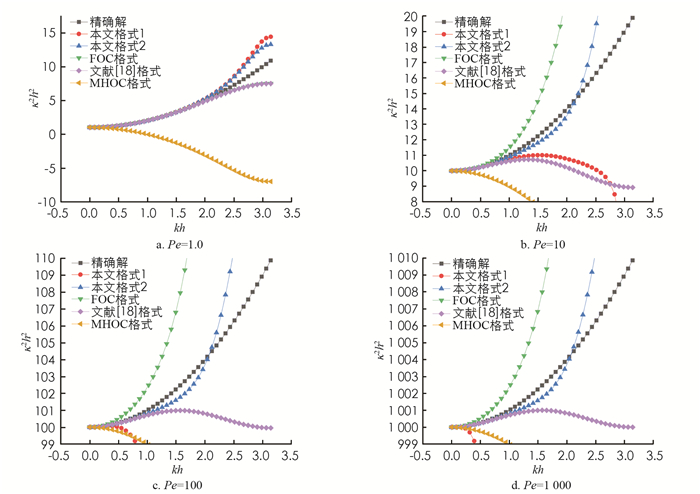
图 1表示了在区间0≤kh≤π上，当Count数确定为常数1.0时，对于不同的网格雷诺数Pe，数值波数和精确波数之间的关系.图中κ²h²表示耗散误差.结果表明：在Pe=1.0时，MHOC格式耗散误差很大，而FOC格式和文献[18]格式的耗散误差曲线完全重合，并且相比其他格式，本文格式1和本文格式2的耗散误差较小；当网格雷诺数Pe从10增大到1 000时，本文格式1的耗散误差逐渐增大，表现出强耗散性，而本文格式2的耗散误差要明显小于其它格式的耗散误差.

图 2表示了在区间0≤kh≤π上，当网格雷诺数Pe确定为常数1.0时，对于不同的Count数，数值波数和精确波数之间的关系.结果表明：对于不同的Count数取值，本文格式1和本文格式2的耗散误差均明显小于FOC格式的耗散误差，并且在高波段上本文格式2的耗散误差小于本文格式1的耗散误差.

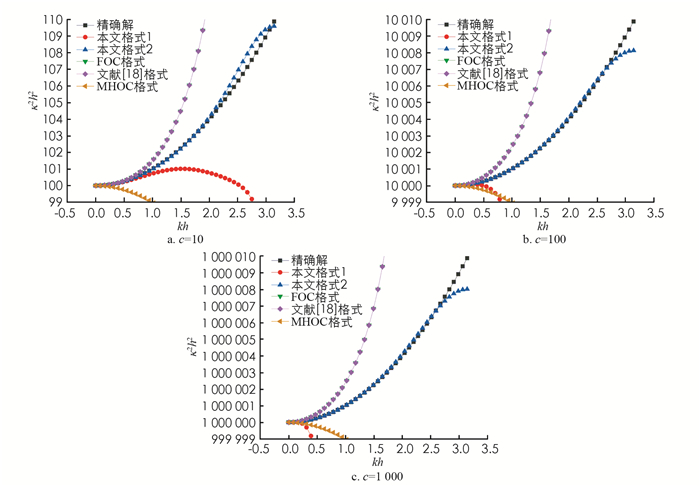
图 3表示了在区间0≤kh≤π上，当Pe数和Count数相等时，对于不同的取值，数值波数和精确波数之间的关系.结果表明：对于不同的取值，在整个波段上，本文格式2的耗散误差很小，而其它4种格式的耗散误差随着Pe数和Count数的增大而增大，表现出强耗散性.特别地，文献FOC格式和文献[18]格式的耗散误差曲线完全重合.

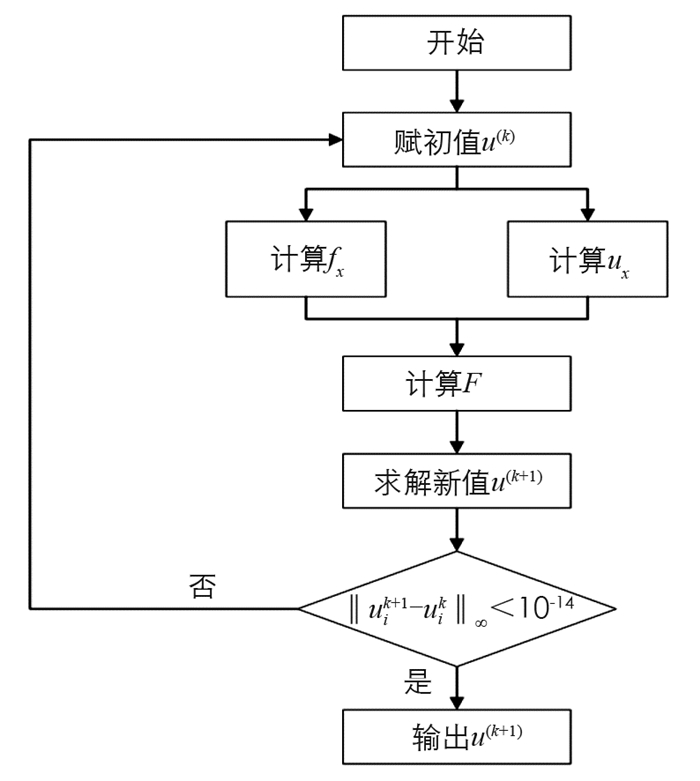
将(16)式和(18)式中的算子展开，差分方程统一写为

其中对应(24)式的系数见(17)式和(19)式.求解算法流程图如图 4所示.

考虑如下二维对流扩散反应问题

其中：ε₁，ε₂为扩散项系数且ε₁，ε₂>0；μ₁和μ₂为对流项系数；b(x，y)为反应项系数；f(x，y)为源项；u(x，y)是未知函数，函数u(x，y)，b(x，y)和f(x，y)在计算区域上足够光滑.

将求解区间[X₁，X₂]等分为N个子区间：x_i=X₁+ih，y_j=Y₁+jh，i，j=0，1，2，…，N，$h=\frac{X_2-X_1}{N}$.

将(25)式改写为如下等价的方程组形式

其中

对(26)式和(27)式应用差分格式(14)得

其中

将(28)式中两项相加得

其中

由

直接计算得

将(35)式和(36)式代入(29)式中得

由

直接计算得

将(38)式和(39)式代入(30)式中得

将(37)式和(40)式相加并整理得

对其中的c₂(-μ₂u_yxxij-b_iju_xxij-2b_xiju_xij)+d₂(-μ₁u_xyyij-b_iju_yyij-2b_yiju_yij)中各项采用二阶中心差分算子离散，对其中的c₁(ε₂u_yyxij-μ₂u_yxij-b_iju_xij)+d₁(ε₁u_xxyij-μ₁u_xyij-b_iju_yij)中各项采用以下四阶差分算子离散

得

将(45)式代入(33)式中并整理得

从而得到模型方程(25)的离散差分格式

其中

(48) 式中右端项中的f_xij，f_yij，f_xxij，f_yyij分别采用一阶导数和二阶导数的中心差分算子计算得到.而u_xij，u_yij采用如下的四阶Padé型紧致差分公式进行离散

离散u_xij和u_yij，边界条件采用文献[20]给出的如下四阶逼近公式，其中α代表x或y.

1) 给u赋初值u_ij⁰，i，j=1，2，…，N；

2) 采用中心差分算子计算f_xij，f_yij，f_xxij，f_yyij；

3) 采用四阶Padé型紧致差分公式(49)和四阶一致边界条件(50)计算u_xij，u_yij；

4) 将以上各量值代入(48)式计算F_ij；

5) 将F_ij代入(47)式中计算u_ij的新值，记为u_ij^k+1；

6) 如果$e r r=\left|\frac{u_{i j}^{k+1}-u_{i j}^k}{u_{i j}^k}\right| \geqslant 10^{-14}$，则将u_ij^k+1赋值于u_ij⁰，重复2)-5)，直到$e r r=\left|\frac{u_{i j}^{k+1}-u_{i j}^k}{u_{i j}^k}\right|<10^{-14}$，输出u_ij.

本节将选取典型算例，采用Fortran95程序语言，在具有4GB内存，Intel(R) Core(TM) i5-7200U CPU处理器的计算机上编制统一程序，采用本文格式和文献格式进行计算，并与精确解进行比较，验证格式的精度.

收敛阶采用如下公式

进行计算，其中：E₁，E₂分别为网格数取N₁，N₂时采用差分格式计算得到的最大绝对误差.

例1^[15]  -u_xx+u_x+u=2sin x+cos x，0 < x<π.

该算例的边界条件为u(0)=u(π)=0.精确解为u(x)=sin x.它在计算区域上是一个光滑函数.表 2给出了在不同网格数下采用以上5种格式计算的最大绝对误差和收敛阶.从表 2中我们可以发现，5种差分格式在粗网格和细网格上均能达到理论上的计算精度，且本文格式1和格式2的误差略小于FOC、文献[18]和MHOC 3种四阶差分格式的计算误差.

例2  -εu_xx-u_x+u=0，0 < x < 1.

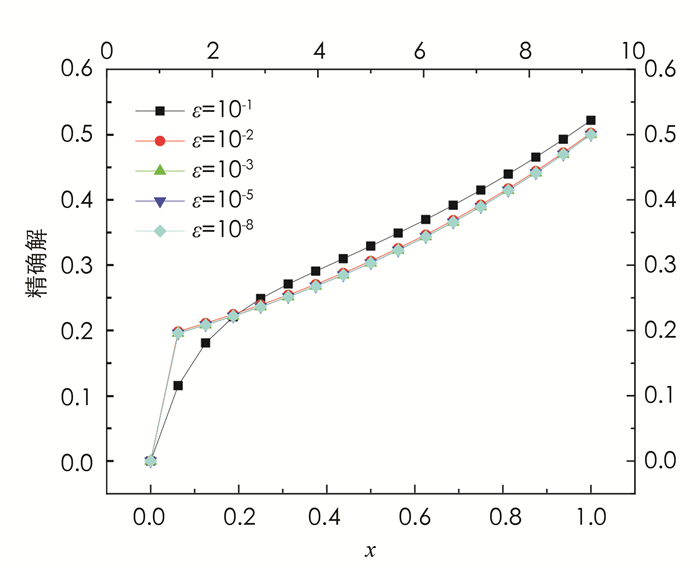
边界条件为u(0)=0，$u(1)=\frac{\mathrm{e}^{m_1}-\mathrm{e}^{m_2}}{\left(1+m_1\right) \mathrm{e}^{m_1}-\left(1+m_2\right) \mathrm{e}^{m_2}}$，精确解为$u(x)=\frac{\mathrm{e}^{m_1 x}-\mathrm{e}^{m_2 x}}{\left(1+m_1\right) \mathrm{e}^{m_1}-\left(1+m_2\right) \mathrm{e}^{m_2}}$.其中$m_1=\frac{-1+\sqrt{1+4 \varepsilon}}{2 \varepsilon}$，$m_2=\frac{-1-\sqrt{1+4 \varepsilon}}{2 \varepsilon}$.

如图 5所示，当网格数N=16时，随着ε的减小，该算例的精确解在计算区域的左端点x=0处有一边界层.表 3比较了当ε=10^-1，10^-2，10^-3时本文格式和文献格式的计算结果.

从表 3可知：

1) 在细网格下，所列格式都能到理论上的收敛阶，但本文两种差分格式的计算精度明显优于FOC格式、MHOC格式和文献[18]格式.

2) 随着ε的减小，本文两种差分格式优势更显著.比如当ε=10^-3，N=512时，采用本文格式1计算得到的最大绝对误差为3.455 2×10^-6，采用本文格式2计算得到的最大绝对误差为2.018 4×10^-6；FOC格式若要得到相同量级的计算精度(此时最大绝对误差为5.446 9×10^-6)，至少需要2 048个网格点；文献[18]格式若要获得相同量级的计算精度(此时最大绝对误差为3.769 7×10^-6)，至少需要3 500个网格点.

3) 当ε很小时，本文格式1在粗网格上的计算误差小于本文格式2，在细网格上的计算误差大于本文格式2.当ε=1和ε=10^-1时，MHOC格式可以达到理论上的四阶精度；但是当ε < 0.065时，不论在粗网格还是在细网格上，MHOC格式都是发散的.

例3 ^[16] -εu_xx-u_x+εu=sin x，0 < x < π

边界条件为u(0)=u(π)=0，精确解为$u(x)=\frac{1}{1+4 \varepsilon^2}\left(A \mathrm{e}^{\frac{r_1 x}{\pi}}+B \mathrm{e}^{\frac{r_2 x}{\pi}}+2 \varepsilon \sin x+\cos x\right)$.其中$r_1=\frac{-\pi\left(1+\sqrt{1+4 \varepsilon^2}\right)}{2 \varepsilon}$，$r_2=2 \pi \varepsilon\left(1+\sqrt{1+4 \varepsilon^2}\right)^2$，$A=\frac{\left(1+\mathrm{e}^{r_2}\right)}{\left(\mathrm{e}^{r_1}-\mathrm{e}^{r_2}\right)}$，$B=\frac{\left(1+\mathrm{e}^{r_1}\right)}{\left(\mathrm{e}^{r_2}-\mathrm{e}^{r_1}\right)}$.

如图 6所示，随着ε的减小，该算例的精确解在计算区域的左端点x=0处有一边界层.表 4中比较了当ε=10^-1，10^-2，10^-3时本文格式和文献格式的计算结果.从表 4可知：

1) 在细网格下，所列格式都能达到理论上的收敛阶，但本文两种差分格式的计算精度明显优于FOC格式、MHOC格式和文献[18]格式.

2) 随着ε的减小，本文两种差分格式的计算误差比所列其它文献格式高出2~6个数量级.当ε=10^-3，N=32时，本文格式1的最大绝对误差为3.664 1×10^-5，本文格式2的最大绝对误差为4.527 8×10^-4；而FOC格式(此时最大绝对误差为3.538 9×10^-4)若要得到相同量级的计算精度，则至少需要4 096个网格点；文献[18]格式若要得到相同量级的计算精度(此时最大绝对误差为5.262 8×10^-4)，则至少需要6 000个网格点.

3) 当ε很小时，本文格式1在粗网格上的计算误差小于本文格式2，而在细网格上的计算误差大于本文格式2.当ε=1时，MHOC格式可以达到理论上的四阶精度；但是当ε < 0.23时，不论在粗网格还是在细网格上，MHOC格式都是发散的.

例4^[21]  -εu_xx-εu_yy+2u_x+u_y=f(x，y)，0 < x，y < 1.

边界条件为$u(0, y)=\mathrm{e}^y+2^{-\frac{1}{\varepsilon}}(1+y)^{1+\frac{1}{\varepsilon}}$，$u(1, y)=\mathrm{e}^{y-1}+2^{-\frac{1}{\varepsilon}}(1+y)^{1+\frac{1}{\varepsilon}}$，$u(x, 0)=\mathrm{e}^{-x}+2^{-\frac{1}{\varepsilon}}$，$u(x, 1)=\mathrm{e}^{1-x}+2$.精确解为$u(x, y)=\mathrm{e}^{y-x}+\left(\frac{1+y}{2}\right)^{\frac{1}{\varepsilon}}(1+y)$.

表 5列出了当ε=1，10^-1，10^-2，10^-3时本文格式和文献格式的最大绝对误差和收敛阶比较.从表 5中数据不难发现，ε越小，本文格式的优势越明显.特别地，当ε=10^-2，10^-3时，本文格式较文献格式在计算精度上要高出1~2个数量级.

例5 -εu_xx-εu_yy-u_x-u_y+εu=sin x+sin y，0 < x，y < π.

边界条件为

精确解为$u(x, y)=\frac{1}{1+4 \varepsilon^2}\left(A\left(\mathrm{e}^{\frac{r_1 x}{\pi}}+\mathrm{e}^{\frac{r_1 y}{\pi}}\right)+B\left(\mathrm{e}^{\frac{r_2 x}{\pi}}+\mathrm{e}^{\frac{r_2 y}{\pi}}\right)+2 \varepsilon(\sin x+\sin y)+(\cos x+\cos y)\right)$.其中$r_1=\frac{-\pi\left(1+\sqrt{1+4 \varepsilon^2}\right)}{2 \varepsilon}$，$r_2=2 \pi \varepsilon\left(1+\sqrt{1+4 \varepsilon^2}\right)^2$，$A=\frac{\left(1+\mathrm{e}^{r_2}\right)}{\left(\mathrm{e}^{r_1}-\mathrm{e}^{r_2}\right)}$，B$B=\frac{\left(1+\mathrm{e}^{r_1}\right)}{\left(\mathrm{e}^{r_2}-\mathrm{e}^{r_1}\right)}$.

表 6列出了当ε=1，10^-1，10^-2时本文格式和文献格式的最大绝对误差和收敛阶比较.从表 6中数据不难看出，当ε=1时，本文格式和文献格式的计算精度相当.但是，当ε=10^-1，10^-2时，本文格式的计算精度远远高于文献格式.

本文基于对流扩散方程的指数型差分格式^[2]，构造了求解一维和二维对流扩散反应方程的四阶指数型组合紧致差分格式，所选取的典型算例的计算结果充分表明对于对流(反应)占优问题，本文提出的差分格式的计算精度要明显高于文献中的多项式格式^[14]和多项式型组合格式^[18-19].