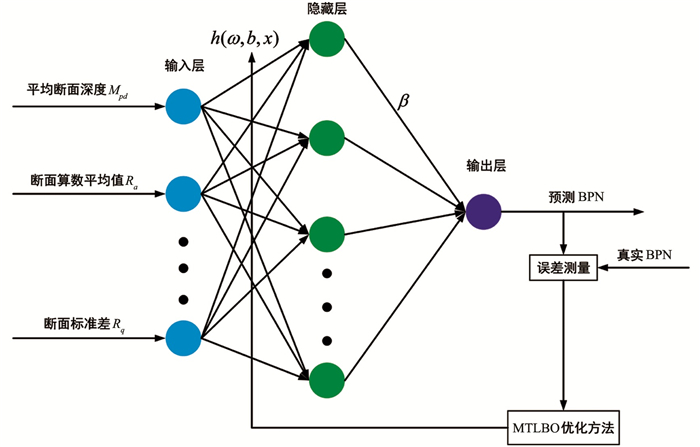
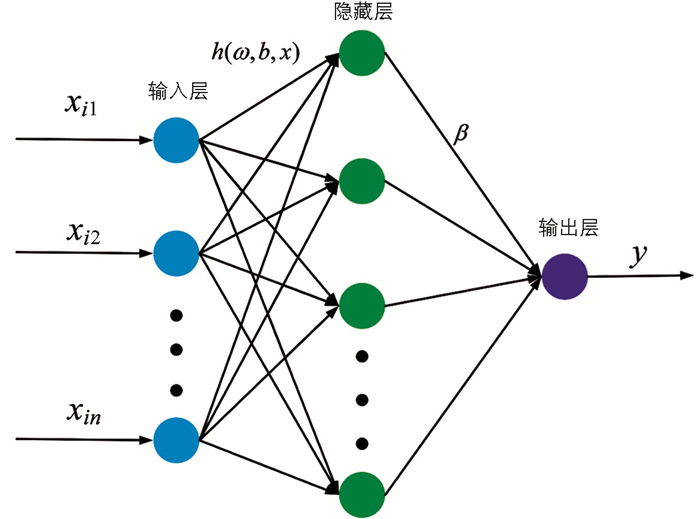
传统的神经网络(Neural Network，NN)技术在速度和准确性方面存在一定的缺点，因此Huang等^[12]提出了名为极限学习机(ELM)的一种单层前馈网络. ELM通常由1个输入层、1个隐藏层和1个输出层组成，如图 1所示. 输入层和隐藏层之间的权重(ω_i)和偏置(b_i)是随机固定的，这种方法减少了计算时间，降低了复杂性，因此其学习速度要比其他传统前馈网络更快. 隐藏神经元用不同的激活函数激活，通常使用高斯激活函数.

ELM输入层、隐藏层和输出层的节点数分别为n、L、m，有N个不同的样本$\left(\boldsymbol{x}_i, \boldsymbol{t}_i\right)$，其中输入$\boldsymbol{x}_i=\left[x_{i 1}, x_{i 2}, \cdots, x_{i n}\right]^T \in \mathbb{R}^n$，期望的输出$\boldsymbol{t}_i=\left[t_{i 1}, t_{i 2}, \cdots, t_{i m}\right]^T \in \mathbb{R}^m$，h(x)为激活函数并在式(1)中描述.

式中：$\boldsymbol{\beta}_i=\left[\beta_{i 1}, \beta_{i 2}, \cdots, \beta_{i m}\right]^T$为第i个隐藏节点到输出节点之间的输出权重矩阵；Y_j为ELM的输出. 式(1)可以由式(2)简单表达.

式中：T为目标输出矩阵；H为隐藏层的输出矩阵，如式(3)所示.

输出权重矩阵可以用式(4)表示：

式中：H⁺为矩阵H的Moore-Penrose广义逆矩阵.

β是对预测准确性影响最大的因素，完全取决于ω_i和b_i. 根据样本的数据特征，通过优化算法决定ω_i和b_i而不是随机选择，可以提高ELM的效率. 在本文中与路面抗滑性能相关性最大的6个宏观纹理参数被视为输入，路面抗滑性能指标BPN被视为ELM预测的目标.

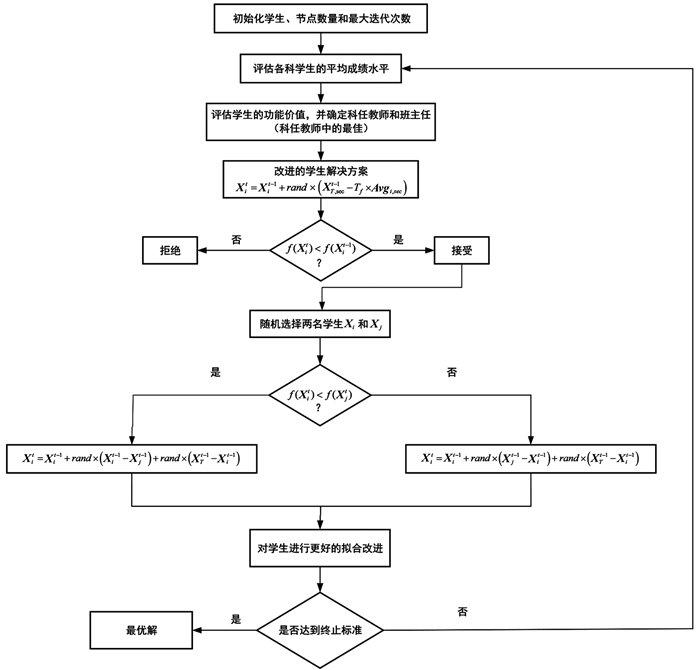
教学优化算法(Teaching-Learning-Based Optimization，TLBO)是由Rao等^[13]基于课堂活动而提出的新型智能算法，其原理是教师对学习者的影响效应. 像其他基于群体的优化技术一样，教师被认为是到目前为止获得的最佳解决方案^[14]. 这一算法主要分为2部分：教阶段，即向老师学习；学习阶段，即通过学习者之间的互动来学习.

在班级中，一个知识渊博的人被指派为班级的教师，他可以根据自身的知识来提高全班的平均成绩. 班级的学生被召集以产生初始班级，$\boldsymbol{X}_i=\left[x_{i, 1}, x_{i, 2}, \cdots, x_{i, D}, \cdots, x_{i, N_P}\right]$，i=1，2，…，N_P，X_i为第i个个体，D为优化问题的维度，N_P为种群规模. 在教学过程中，Avg_i是学习者在单一科目中的平均成绩. 在班级中成绩较好的学生被选为最有知识能力的人(X_T^t)，他推动了所有学生的平均成绩. t是当前的迭代次数，X_T^t为t次迭代下的教师，X_T^t试图将平均值Avg_i移向自己的水平，即学生们在教师的帮助下更新他们的成绩，以提高平均成绩，如式(5)所示.

式中：rand为[0, 1]上的随机数；T_f为教学因子，决定要改变的平均值，T_f的取值为1或2. 这是一个启发式的步骤，以相等的概率随机决定，如式(6)所示.

式中：round代表四舍五入取整.

在学习阶段，学习者可以在其他学生的帮助下提高自己的知识水平，以提高平均成绩. 如果共同学习者与自己相比知识更丰富，学习者就可以扩大自己的知识^[15]. 学生之间改变立场的互动在式(7)中描述.

在TLBO算法中，提高整个班级在教阶段的表现，教师是一个重要的影响因素. 为了提高TLBO算法的探索能力，对TLBO的教阶段进行修改. 在这项工作中，班级被分成不同的部分. 学生按照他们的函数值被缩短，成绩最高的学生(较好的函数值)被分配为某一区的教师. 在每个部分，学生被随机分配. 学生们通过让出相应的教师X_T，sec^t来更新他们的位置，如式(8)所示.

式中：Avg_i，sec是一个特定部分学生的平均成绩.

通过这种方法，该算法的局部搜索能力得到了加强，这有助于增加解决方案的多样性. 在TLBO算法中，所有的学生都朝一个方向(朝向教师)迁移，这可能会误导整个班级，这个问题可以通过分配部分教师来解决^[11].

在TLBO算法的学习阶段，学生们通过相互交流不断地修正教师的位置，式(7)通过纳入教师的优势而被修改为式(9).

在每次迭代中，一些呆板的学生会被其他一些学生淘汰(随机初始化学生). 学生的淘汰在式(10)和(11)中描述. 图 2为MTLBO算法的流程图.

式中：N为要淘汰的学生人数；X_i(N)是要考虑的新学生；LB和UB是下边界和上边界；o^t是一个常数，与迭代的次数成比例衰减.

ELM通常是分类和回归的首选，其性能比NN更好. ELM的性能可以通过适当地调整相关的输入权重、偏置和隐藏神经元的数量来提高. 因此，本文通过MTLBO算法适当决定ELM的相关输入权重和偏置来最小化预测误差.

MTLBO-ELM预测模型中优化算法只在训练ELM模型时使用. ELM的相关参数是在训练模型期间由MTLBO优化算法决定，使得预测误差最小. MTLBO的首要目标是通过适当选择ELM的输入层权重和偏置实现训练误差最小化，具有这些参数的ELM模型被用于测试数据集.

本文利用MTLBO方法优化ELM模型参数的流程如图 3所示，选取路面试样随时间变化的宏观纹理表征指标平均断面深度M_pd、断面算数平均值R_a、断面标准差R_q、极差R_z、驼峰度R_ku、偏斜度R_sk作为MTLBO-ELM的输入，抗滑性能BPN作为MTLBO-ELM的输出，即预测量. 在模型训练过程中将ELM预测的BPN与真实值之差输入到MTLBO的优化算法中，从而实现动态调整ELM输入层与隐藏层之间的权重和偏差，通过MTLBO优化算法获得的参数能够有效提高ELM预测的泛化性和准确性.

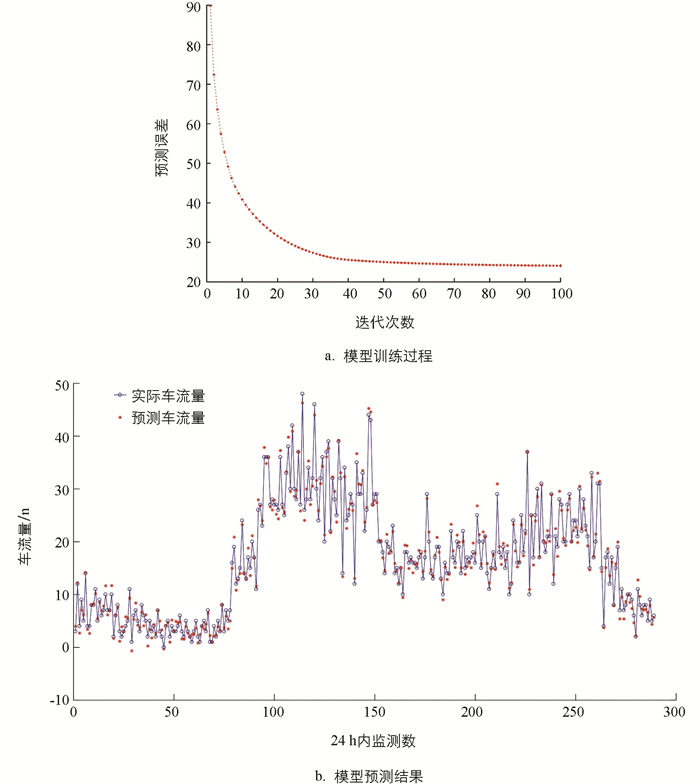
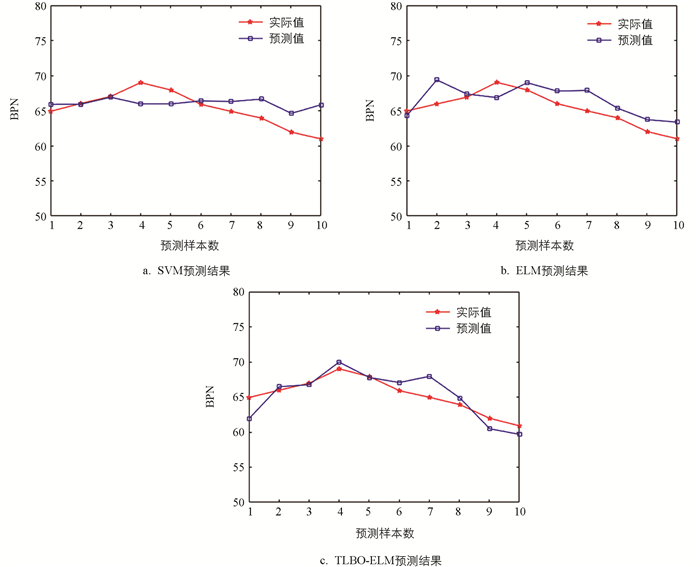
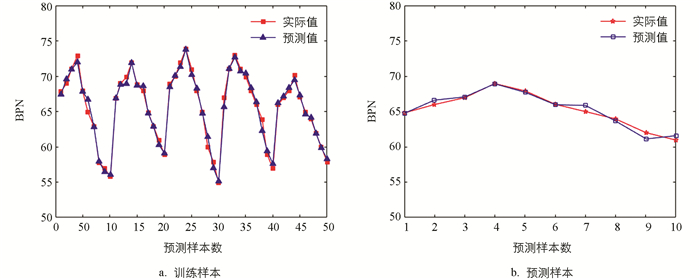
为验证本文所提出模型的有效性，首先选取某道路交通流量数据进行车流量预测. 本文一共采集了1年内的交通流量数据，每隔5 min记录1次该时间段内的车流量数据. 本文截取5 d的车流量数据，利用前4 d的车流量数据训练MTLBO-ELM模型，最后用训练好的MTLBO-ELM模型去预测第5 d的车流量. 同时利用相同的数据集通过SVM、ELM和TLBO-ELM进行训练，并预测第5 d的车流量.

图 4为MTLBO-ELM模型训练过程和预测结果，表 1给出不同预测模型对交通流量数据的精度比较. 表 1中MTLBO-ELM模型的RMSE为0.583 7，R²为0.935 9，在对比模型中其评价指标最好，由此可见MTLBO-ELM模型的泛化能力较强. 因此，通过交通流量数据集预测结果，证明了MTLBO-ELM模型的有效性，为接下来的道路表面抗滑性能预测奠定了基础.

沥青路面在经过车辆的反复碾压之后，沥青表面的沥青膜剥落，路面骨料裸露出来，路面的抗滑性能到达峰值；继续经过车辆的反复碾压，骨料被抛光，路面抗滑性能出现一定的衰退. 为研究这一衰变过程的规律，在实体道路上长期监测路面的抗滑性能有诸多限制，因此本文通过加速加载器在实验室内模拟路面抗滑性能衰变的过程.

为了能模拟出在车辆反复碾压下真实路面抗滑性能的变化，本实验采用了MMLS3载荷模拟器，图 5为其实物图. 该设备可以在7 200次轮载/小时、2.7 kN的最大轮载下进行实验. 将试样放入该设备中，到达相应轮载荷次数后，将试样取出，完成各项指标的记录，将试样放回并进行下个阶段的载荷实验^[16].

根据某道路的沥青比配比制作了6个路面试样，其中一试样如图 6所示. 加速加载器的加载参数设置为5 200次轮载/小时，小轮与路面试样间的压力为标准轴载0.7 MPa. 按照表 2所示的记录周期对试样进行监测. 为了能够真实还原路面的使用情况，在各个加载周期内按照实际道路的养护标准进行洒水养护，从而能够真实地体现出路面抗滑性能的衰变过程^[17].

将路面样本在不同轮载荷次数下的表面变化直观记录下来，如图 7所示. 在图 7中可以明显地观察到路面试块的颜色和抛光度发生了明显的变化.

沥青路面纹理可以用多种指标来进行表征，主要指标如表 3所示. 本文只利用与路面抗滑性能相关性最大的纹理指标构建预测模型.

沥青路面主要有BPN和横向力系数(Sideway Force Coefficien，SFC)两项抗滑指标来表征路面抗滑性能^[18]，本文所要预测的抗滑指标BPN由摆式仪测得. 摆锤的回摆高度可直接从仪器上读出，即摆值的大小. 我国规定高速公路、一级公路的BPN一般大于45^[19].

对表 3中的各项路面纹理指标与BPN进行相关性分析，筛选出如下路面纹理指标用来对BPN进行多元预测.

(1) 平均断面深度M_pd

根据ISO13743-1规定在计算M_pd时断面的水平长度需要超过100 mm，将断面分为2部分，式中peak(1st)为第1部分的峰值；peak(2nd)为第2部分的峰值；Average为整个断面的平均高度.

(2) 断面算数平均值R_a

(3) 断面标准差R_q

(4) 极差R_z

(5) 驼峰度R_ku

(6) 偏斜度R_sk

式中：n为断面轮廓采样点数；Z_i为第i个测量点的高度；Z为n个测量点的平均高度；σ是Z的标准差.

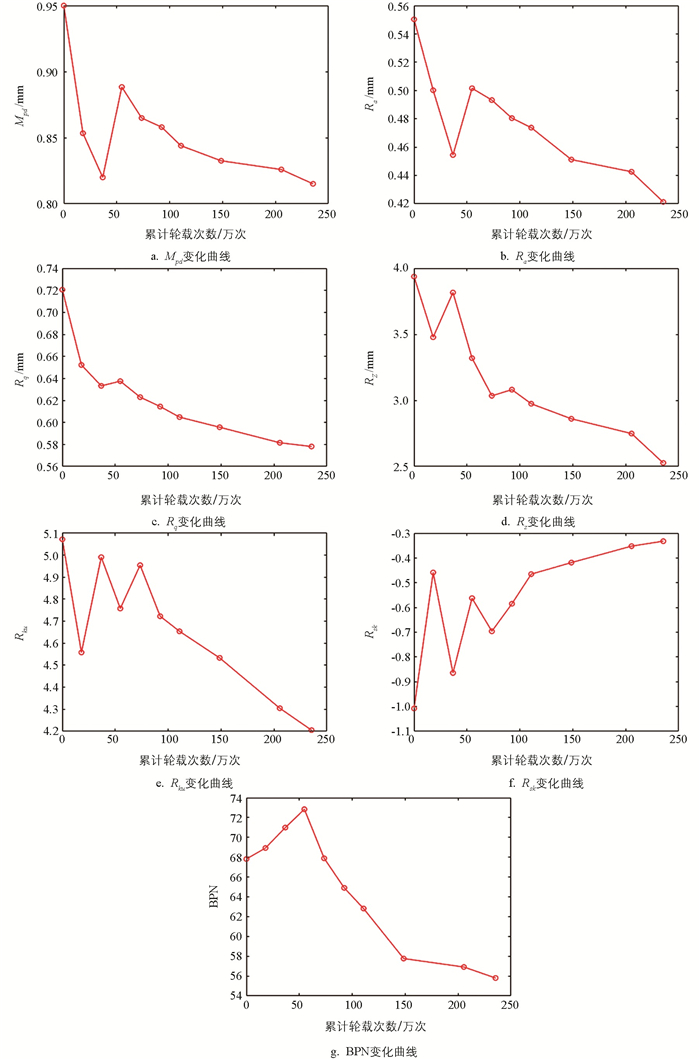
为了进一步表明图 7的微观变化，将其中某一试样的各项相关性指标的变化曲线表示出来，如图 8所示. 从图 8的曲线中可以明显地观察到路面随着轮载次数的增加，其纹理特征值和BPN也会发生明显的变化.

选取实验当中路面试样随时间变化的宏观纹理表征指标平均断面深度M_pd、断面算数平均值R_a、断面标准差R_q、极差R_z、驼峰度R_ku、偏斜度R_sk作为MTLBO-ELM的输入，抗滑性能BPN作为MTLBO-ELM的输出，即预测量. 用前5组路面试样的监测数据作为模型的训练，最后一组路面试样的监测数据作为测试，即训练样本数为50，预测样本数为10.

本文使用了3种常用的预测方法进行比较，即支持向量机SVM，极限学习机ELM，基于教学优化的极限学习机TLBO-ELM. 图 9为3种常用预测模型的预测结果. 图 10为本文所提出的MTLBO-ELM模型的预测结果.

为了定量评价本文提出方法与其他常用模型对多因素影响下沥青路面抗滑性能预测结果的好坏，本文用均方根误差(RMSE)和预测样本复相关系数(R²)作为定量分析的指标. 表 4为各预测模型的预测结果精度比较.

由表 4可知，ELM模型在路面抗滑性能预测上比SVM有更出色的表现，进一步通过优化算法探索ELM的相关参数，TLBO-ELM的性能得到了提高. 本文所提出的MTLBO-ELM模型的RMSE为0.5032，R²为0.95. 从评价指标的角度，本文提出的MTLBO-ELM预测模型在路面抗滑性能预测方面具有更好的性能.

1) 采用MMLS3加速加载实验装置模拟了6个沥青路面试样在车辆载荷作用下微观纹理、抗滑性能BPN、外貌形状和颜色的变化规律. 实验结果表明，沥青路面在建设完成投入使用的前期，因车轮的反复碾压，表面的沥青剥落，骨料裸露，导致抗滑性能增加；随着碾压次数的加大，表面骨料被抛光，抗滑性能出现一定的下降；

2) 利用沥青路面的宏观纹理指标平均断面深度M_pd、断面算数平均值R_a、断面标准差R_q、极差R_z、驼峰度R_ku和偏斜度R_sk去预测路面抗滑性能指标BPN，具有可行性；

3) 通过对基本TLBO算法中的教阶段和学习阶段进行改进，进一步提高了TLBO算法的局部搜索能力. 利用改进的TLBO算法优化ELM预测模型的相关参数，固定具体参数后的ELM在路面抗滑性能预测方面性能出色. 该模型对沥青路面抗滑性能的评价具有一定的指导意义.