-
目前先进的遥感应用都需要高空间分辨率的光谱图像,这使得高空间分辨率光谱图像变得越来越重要[1-2].由于卫星传感器设计的物理和技术限制,使得需要花费更高成本才能获得具有高空间分辨率的多光谱图像[3].为了补偿光谱图像的低空间分辨率,遥感卫星通常提供互补的高空间分辨率全色(HRP)图像[4].遥感图像Pan-Sharpening融合是一个很有前景的领域,其目标是利用HRP图像的空间信息来增强光谱带的空间分辨率[5-6].
关于Pan-Sharpening的研究大体可分为4大类,包括:基于组分替换的方法[7]、基于多分辨率分析(MRA)的方法[8]、基于模型的方法和基于超分辨率的方法[9].文献[10]提出了基于组件替换的多光谱和全色图像融合的优化模型来获得自适应权重.
通过最大化目标函数来计算自适应权重,该目标函数测量低分辨率图像和Pan图像之间的辐射度相似性.文献[11]提出了一种基于正则化模型的Pan-Sharpening优化框架,创新处为:引入了新的正则化项和高通滤波器,与用于低分辨率光谱观察的低通滤波器互补,引入了对应于全色观察模型的残余误差.
目前,超分辨率融合方法正成为提高多光谱图像空间分辨率的有效方法[12].在Pan-Sharpening中,传统的基于超分辨率的方法是基于重建和压缩感知方法[13].基于重建的方法基于实施重建约束并对高分辨率(HR)数据施加后验知识;基于压缩感知的超分辨率方法是Pan-Sharpening的一个热门研究方向.由于压缩传感理论具有从压缩的HR图像中恢复未知HR图像的强大功能,基于该理论已经有大量的泛锐化研究.文献[14]提出了一种HRP和LRM图像融合的稀疏表示方法,首先通过加性小波融合方法获得(high-resolution multi-spectral,HRM)图像,然后设计线性约束K-SVD方法来训练字典以提高其表示能力.文献[15]将Pan-Sharpening模型化为图像恢复问题,使用稀疏性和局部自回归模型正则化,使用K-SVD算法构造两个字典,最后重建HRM图像.基于重建和压缩感知的方法虽然具有良好的性能,但是高度依赖于先验,并且当上采样因子很大时,性能被降低.
为了解决上述问题,本文引入了基于学习的方法,其目的是恢复LR输入图像中不存在的细节.该方法的基本假设是可以从一些LR-HR补丁对中学习缺失的细节.为了实现基于学习的算法,学习可用数据的HR-LR图像块之间的映射,然后将该映射应用于LR图像以获得其HR图像.目前的方法仅使用LR输入图像及其底层图像来恢复HR图像[16],导致在构建HRM图像时性能受到影响.
针对以上问题,本文提出了一种基于多尺度金字塔的多光谱图像Pan-Sharpening方法,该方法利用HRP图像中的冗余补丁作为重建HRM图像的内部源样本.首先,从低分辨RP图像创建金字塔;然后,通过利用该金字塔作为指导并考虑同一级别以及较低级别中每个补丁之间的关系,重构上采样的LRM频带;最后,从上采样的多光谱带估计高分辨率强度分量.本文的方法能有效地保留源图像的光谱和空间信息.
全文HTML
-
对于更符合人类视觉的IHS空间域(代表强度、色调和饱和度的空间域),高分辨率Pan图像代替IHS空间域中的强度分量I,即为I′,最后逆变换得到RGB空间的融合图像,这个过程为Pan-Sharpening,数学描述过程为
其中I表示IHS空间域中的强度分量,d1和d2表示两个过渡分量,则有
Pan图像代替强度分量I,表示为
其中,
$\mathrm{M=}\left( \begin{matrix} 1 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ 1 & \sqrt{2} & 0 \\ \end{matrix} \right)$ ,$\left( \begin{matrix} {{R}'} \\ {{G}'} \\ {{B}'} \\ \end{matrix} \right)$ 表示融合后图像的RGB波段矩阵. (3)式说明原始RGB图像可以通过加法运算得到融合图像.全景锐化任务的主要目的是保持融合图像的统一空间光谱保真度.对于具有S个光谱带的低分辨率图像,将全色锐化结果表示为FMS,这是对地面实际情况fMS的估计.多光谱(multi-spectral,MS)图像全色锐化的约束函数表示为
其中,P(·)表示Pan-Sharpening过程,gMS表示低分辨率MS图像的降级观测图像,gPan表示Pan图像.融合过程在线性框架下模拟为
其中,D是空间域中的下采样矩阵;R是传感器的Pan信道的频谱响应矩阵,其沿着频谱对潜在地面实例进行下采样;H是模糊矩阵;NMS和NPan是加性噪声,假设是高斯分布的.对于Pan-Sharpening重构强度分量通过下一节中多尺度金字塔方法得到.
-
输入图像具有足够的自相似信息,可以从大尺度图像中获得小尺度图像的高频信息,可以使用多帧输入图像来精确重建图像.因此,当外部图像不能被访问时,提出了一种多尺度金字塔方法.该方法通过逐步构造大尺度图像来加入训练集,可以从不同比例的图像中充分了解所有冗余信息.首先给出多波段和全色图像融合框架HIS和类HIS框架
其中FH和BL,up分别表示融合LRM图像和上采样LRM图像,L是光谱频带的总数,PH是高分辨率全色数据,IH是高分辨率强度分量.目的是有效地估计LRM和HRP图像的高分辨率强度分量IH.
为了以HRP数据的空间结构为指导获得上采样的多谱带,提出一个多尺度金字塔方法.首先通过多尺度方案对LRM波段进行上采样,然后通过估计的上采样LRM和HRP图像得到高分辨率强度分量.IH的质量取决于从现有的LRM数据和HRP数据中准确提取的LRM样本.
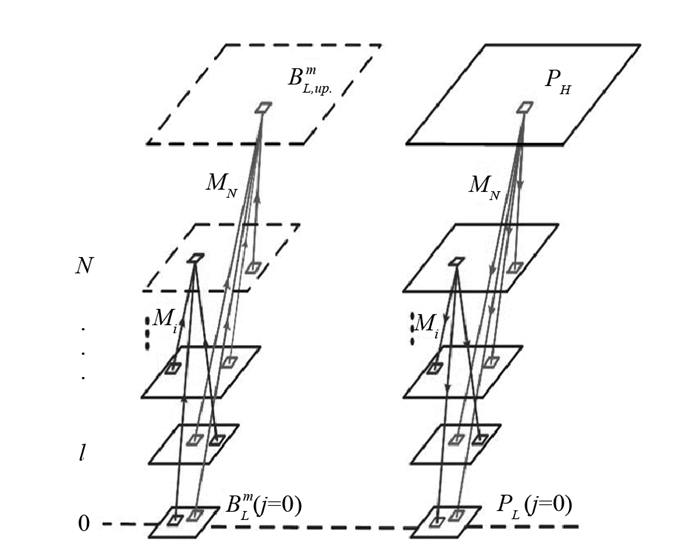
从BL中重建BL,up,其解决方案是模仿高分辨率和低分辨率的全色数据之间的结构关系,即HRP数据可以从较低分辨率的图像中得到较强的恢复,而将提取的关系扩展到较低尺度的LRM波段,可以准确地得到所需的上采样多光谱波段BL,up. 图 1展示了多尺度金字塔方法,可以得到从现有的LRM和HRP图像上采样的多光谱波段的重建强度分量.
如图 1所示,首先尝试通过低分辨率图像重建可用的HRP图像(低分辨率全色数据记为PL).为此,LRP和HRP图像之间的隐藏层被分解为N级.利用抽取算子得到低分辨率RP图像,抽取过程由模糊和降采样组成.步长为(Lx,Ly)的下缩放取决于层数(N),可以写成
其中,(dx,dy)是HRP图像的尺寸,ρ是HRP和LRM数据之间的空间比率.
HRP金字塔的第j层划分为n×n补丁并且被安排在一个矩阵Djp=(xP,j1,…,xP,jK)中,其中K是总数的补丁级别.基于学习的方法是从第j层(j∈{1,…,N})的低尺度重构每个补丁,可表示为DjP= D0P∪…∪ Dj-1P,其中,P表示HRP数据.
基于欧几里德距离,在DPj中找到xP,ji并排列在SPj中.同样,从DPj中选取的补丁是从DBj中提取出来的,用SBj表示(DBj是一个矩阵,包含LRM金字塔第j层图像中的所有n×n补丁).利用{1,…,j}层上采样全色图像和{1,…,j-1}层上采样多光谱图像来构造第j层多光谱图像.
由于HRP图像的强大的空间细节,这个过程被认为是作为重建未知HR强度分量的指导.因为多光谱带与全色图像之间的结构相似性,可以找到一个HRP金字塔补丁xP,ji和LRM图像补丁xB,ji之间的关系来预测高分辨率,并使用这些关系到其它波段.映射函数为
SPj中含有相似的补丁xP,ji,同样SBj中含有相应的选定补丁SPj.为减小奇异性,将Tiknonov正则化为
其中λ是一个正值,被称为正则化参数. (9)式的解可以由(10)式给出:
第j层上采样多光谱带通过拼接补丁来构建,使用分段过程对LRM图像进行采样.然而,分段分析可能不能满足全局重构,即在重建下一个金字塔级别之前,应该使用一个全局项来保证每个步骤结束时重建的上采样多光谱带与其LR图像的一致性:
其中,t表示迭代索引,τ表示步长.可以通过(13)式生成IH为
其中,W表示权重向量.
1.1. 基于IHS的Pan-Sharpening线性模型
1.2. 多尺度金字塔方法
-
本文的实验对象是GeoEye-1和DEIMOS-2收集的两个数据集.数据集中包括不同结构的图像,如建筑物、植被、土壤和道路等,且两个数据集的分辨率ρ均为4.为了验证本文方法的有效性,将本文方法与其它方法进行性能比较,其它方法包括:主成分分析法(Principal Component Analysis,PCA)、GS法(Gram-Schmidt)、修正的亮度色度饱和度方法(modified intensity-hue-saturation,MIHS)和两步稀疏编码方法(Two-step sparse coding,TSSC)[9].
本文实验性能指标有:相关系数(correlation coefficient,CC)、光谱角(spectral angle mapper,SAM)、相对多维尺度误差(Relative Global Dimensional Synthesis Error,ERDAS)和通用图像质量指数(universal image quality index,UIQI).采用不需要参考图像的质量度量(QNR)对融合图像进行质量评价,得到由Ds表示的空间失真和由Dλ表示的光谱失真指数.在本文的方法和TSSC方法中,以7×7的大小提取补丁,重叠区域大小为4,还有金字塔层数N设置为3,数量类似的补丁设置为10,源图像是256*256*4的MS图像,迭代次数t设置为50,迭代步长设置为1.
5种不同的Pan-Sharpening方法与GEOYEY-1数据集的融合结果如图 2所示.
从图 2中可以看出:图 2(d)和图 2(e)中PCA和GS方法在保持源图像的空间信息的同时,严重地扭曲了光谱信息,箭头表示的建筑物是低光谱保存的例子;图 2(f)中MIHS方法比PCA和GS方法保存了更多的空间信息和光谱信息;虽然图 2(g)中TSSC方法保持了较好的光谱信息,但它引入了几个模糊边缘,在TSSC方法的结果中,由矩形限制的边缘区域中的频谱失真较为严重;与其它方法相比,图 2(h)中本文方法保留了更多的空间和光谱信息,特别是在边缘区域,表现出了更优越的性能.
本文所用的第二个数据集是由DEIMOS-2采集的数据集,包括建筑物、道路和植被区域. DEIMOS-2数据集的融合结果如图 3所示.
可以看出:将图 3(d)和图 3(e)中PCA和GS方法融合的结果与图 3(c)中参考图像进行比较,很明显其颜色失真了;其它方法都很好地保存源多光谱数据的光谱信息;然而,图 3(f)中MIHS方法的空间信息略优于图 3(g)中TSSC方法,图 3(g)中矩形的区域说明TSSC方法保留了较少的空间信息;图 3(h)中本文方法保留了更多的空间和光谱信息,特别是在边缘区域,其性能优于其它方法.
对GEOEye-1数据集和DEIMOS-2数据集中图像进行实验,得出不同方法下融合图像的平均性能. 表 1是不同方法下GEOEye-1数据集的对比结果,表 2是不同方法下DEIMOS-2数据集的对比结果. Full Scale指标包括QNR,Ds和Dλ,低分辨率指标包括CC,SAM,ERDAS和UIQI.
从表 1、表 2中数据可以看出,定量评估结果与Full Scale和Degraded Scale的视觉比较是一致的.本文方法在ERGAS,CC,UIQI,SAM这些Degraded Scale性能以及QNR,Ds和Dλ这些Full Scale指标方面都优于其它几种方法,说明本文方法的有效性.
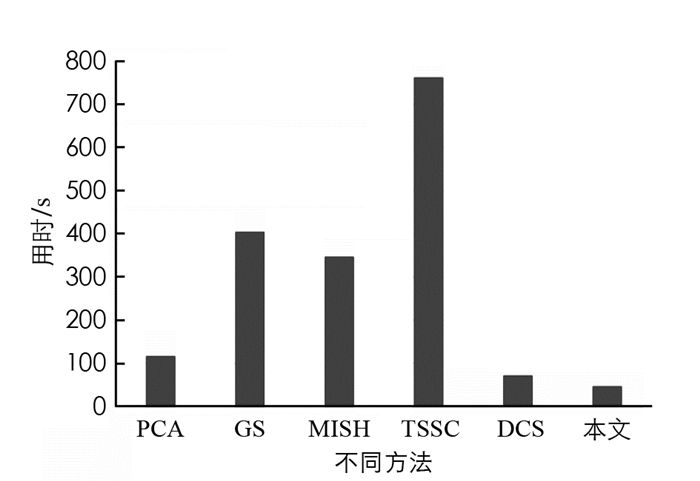
图 4给出了不同方法的时间性能比较,对比方法除了上文的4种方法,再加上文献[17]中分布式压缩感知(Distributed compressed sensing,DCS)方法,图像使用DEIMOS-2数据集中100幅图像,实验结果是100幅图像实验用时的平均.
可以看出:TSSC方法用时最多,这是因为用到两步稀疏编码,导致时间复杂度增加;本文方法用时最少,这是因为本文方法中使用了图像的自相似性,大大减少了时间复杂度.说明本文方法在时间复杂度上的优越性.
-
本文提出了一种多尺度金字塔多光谱Pan-Sharpening方法,用于从可用的LRM和HRP数据中估计强度分量.在强度分量的重建中使用HRP及其低分辨率RP图像减小HRP和强度分量之间的不相似性,减少了传统方法中发生的频谱失真和空间失真.实验结果从视觉和性能上对本文方法进行了验证,本文方法能够减少Pan-Sharpening的光谱和空间失真,性能优于现有其它方法,说明了本文方法的有效性.



 下载:
下载: