本文考虑的捕食者-食饵系统具有两个特征：功能反应函数为比率依赖型；捕食者具有可替换的食物源.此系统的时间连续模型表达式如下^[7]：

其中：u(t)和v(t)分别表示食饵和捕食者在时间t的密度； $\alpha = \frac{{puv}}{{mu + nv}}$ 表示具有比率依赖型的功能反应函数； $bv\left( {1 - \frac{v}{{{k_2}}}} \right)$ 表示捕食者具有可替换的食物源；a和k₁表示食饵内禀增长率和环境容纳量；b和k₂表示在食饵u不存在时捕食者的内禀增长率和环境容纳量；p和e表示捕食率和转化系数；m和n表示半饱和常数；d表示捕食者的死亡率；a，k₁，b，k₂，p，e，m，n，d都是正常数.

令

则系统(1) 可简化为如下无量纲形式：

对系统(2) 应用Euler公式，则可以得到如下时间离散捕食者-食饵系统的映射表达式：

其中τ＞0是时间步长.利用映射不动点的定义^[8]，可求得时间离散捕食者-食饵系统的4个非负不动点如下：

其中u^*是以下二次方程的正实根

且

可以确定映射(3) 的正不动点(u₃＞0，v₃＞0) 存在的充分条件.若映射(3) 中的参数满足如下不等式

则此映射有一个正的实不动点(u₃，v₃).

定理1  1) 不动点(u₀，v₀)在任意参数条件下都不稳定；

2) 当β+α-δ＜0且0＜τ＜min $\left( {2,{\rm{ }} - \frac{2}{{\beta + \gamma - \delta }}} \right)$ 时，不动点(u₁，v₁)稳定；

3) 当α-ε＜0，δ-β＜0且0＜τ＜min $\left( { - \frac{{2\alpha }}{{\alpha - \varepsilon }}, - \frac{2}{{\delta - \beta }}} \right)$ 时，不动点(u₂，v₂)稳定；

4) 当q＜1且-(1+q)＜p＜1+q时，不动点(u₃，v₃)稳定，其中

证 不动点的稳定性可以采用判断差分系统稳定性的Jury判据来分析.映射(3) 在任一点(u，v)的雅克比矩阵表达式为

矩阵(9) 在(u₀，v₀)处的特征方程为λ²-(2-τ(1+β-δ))+|J_(u0，v0)|=0，特征值为λ₁=1+τ，λ₂=1+(β-δ)τ，其中λ₁＞1，故可知不动点(u₀，v₀)不稳定，此结果对任意参数条件都成立.

对于不动点(u₁，v₁)，雅克比矩阵为

其两个特征值为λ₁=1-τ，λ₂=1+τ(β+α-δ)，当β+α-δ＜0，0＜τ＜min $\left( {2,{\rm{ }} - \frac{2}{{\beta + \gamma - \delta }}} \right)$ 时，|λ₁|＜1，|λ₂|＜1，不动点(u₁，v₁)稳定.不动点(u₂，v₂)对应的雅克比矩阵为

其两个特征值为 ${\lambda _1} = 1 + \tau - \frac{{\tau \varepsilon }}{\alpha }$ ，λ₂=1+τ(δ-β)，当α-ε＜0，δ-β＜0，0＜τ＜min $\left( { - \frac{{2\alpha }}{{\alpha - \varepsilon }}, - \frac{2}{{\delta - \beta }}} \right)$ 时，|λ₁|＜1，|λ₂|＜1，不动点(u₂，v₂)是稳定的.

同理，不动点(u₃，v₃)对应的雅克比矩阵的两个特征值为

其中p和q的表达式见公式(7)，(8).当q＜1，-1+q＜p＜1+q时，|λ₁＜|1，|λ₂|＜1，不动点(u₃，v₃)是稳定的.

时空离散捕食系统的Neimark-Sacker分岔及其产生条件可以通过Neimark-Sacker分岔理论^[9]来分析.离散系统在(u₃，v₃)处产生Neimark-Sacker分岔的第一个条件要求公式(12) 中λ₁和λ₂是一对模为1的共轭复数.复数特征值要求p²-4q＜0，即

另外，当q=1满足时，也就是

其中

两个复数特征值满足|λ₁|=|λ₂|=1.

通过下式将(u₃，v₃)平移至原点

则映射(3) 可转化为

式中O((|x|+|y|)⁴)表示以(x，y)为变量且阶数至少为4的多项式函数；映射中的系数表达式如下：

在满足条件(13) 和(14) 的前提下，映射(16) 的不动点(0，0) 对应雅克比行列式的特征值也是模为1的共轭复数.将两个特征值写成

式中 ${\rm{i = }}\sqrt { - 1} $ 并且

Neimark-Sacker分岔的第二个条件要求满足

以及

公式(21) 等价于p(τ₀)≠-2，0，1，2.应该注意到在公式(17) 中p²(τ₀)≠4.因此，p(τ₀)≠-2，2，于是公式(21) 变成p(τ₀)≠0，1，即

接下来研究映射(16) 的规范型，应用变换如下：

那么映射(16) 变成

式中

为使映射(24) 在不动点(0，0) 附近产生Neimark-Sacker分岔，下面的a必须不为零^[10]：

其中

并且 $F\left( {\tilde x,\tilde y} \right)$ 和 $G\left( {\tilde x,\tilde y} \right)$ 在(0，0) 处的二阶和三阶偏导数为

经计算得

其中：

定理2 当条件(13)，(14)，(20)，(22) 和(28) 成立时，时空离散捕食者-食饵系统在(u₃，v₃)附近发生Neimark-Sacker分岔.如果a＜0以及d＞0，则Neimark-Sacker分岔是超临界的，(u₃，v₃)失去其稳定性并在离散系统中产生吸引不变环.

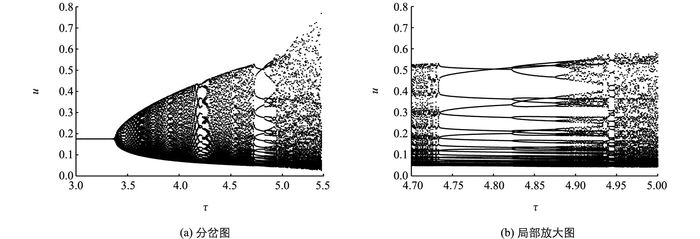
根据以上理论结果，本节通过数值模拟展现参数变化时离散捕食系统的Neimark-Sacker分岔以及由分岔所引起的复杂动力学行为.根据文献[7]，在数值模拟中α=0.91，β=0.03，γ=0.15，δ=0.05，ε=1.0为固定参数，τ为变化参数. 图 1(a)展示了映射(3) 随着参数τ变化的分岔图，分岔图模拟的初始值为(1.01u^*，1.01v^*).在给定参数条件下，可以确定Neimark-Sacker分岔的临界τ值为τ=3.374 4. 图 1(b)是对图 1(a)的局部放大，展示了离散系统趋于混沌过程中产生的倍周期分岔过程.

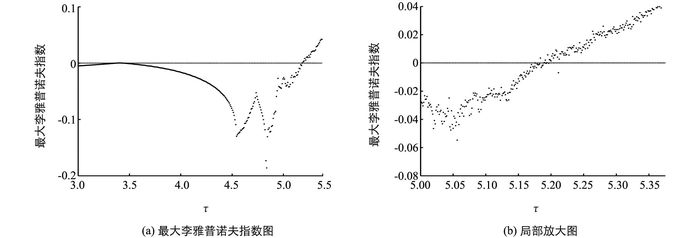
图 2(a)展示了对应于图 1(a)的最大李雅普诺夫指数图.从图 2(a)可以看出，随着参数τ的增大，映射(3) 最终会展现出混沌行为. 图 2(b)为图 2(a)的局部放大图，展示了最大李雅普诺夫指数大于0的点.从图 2(b)可以看出，离散捕食者-食饵系统的混沌行为大约起始于τ=5.19附近.

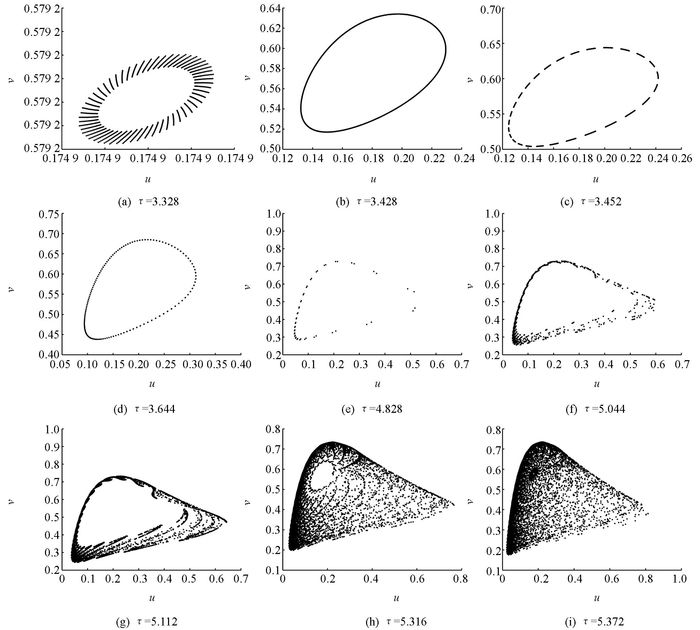
图 1和图 2揭示了Neimark-Sacker分岔开启了一条通往混沌的路径.在此混沌路径上，离散系统的吸引子随着参数而发生改变.映射(3) 展示了随着τ值的增加，系统的吸引子从不动点(图 3(a))到混沌(图 3(b))的转变过程，中间经历了不变环(图 3(b)-(d)，(f)-(g))，以及在不变环区的周期窗口(图 3(e)).

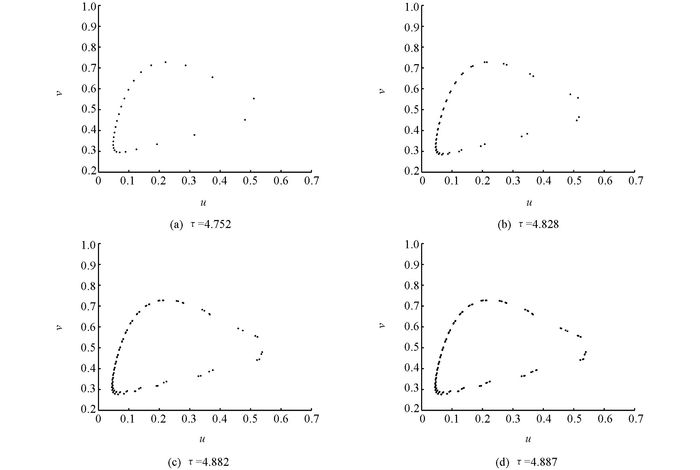
由Neimark-Sacker分岔所引起的混沌路径上也会产生倍周期分岔. 图 4揭示了离散捕食者-食饵系统的一个倍周期分岔过程.如图 4所示，系统从周期-34轨道(图 4(a))出发，经历倍周期分岔转变为周期-68轨道(图 4(b))，再到周期-128轨道和周期-256轨道(图 4(c)和图 4(d)).在经历此倍周期过程之后，系统行为重新进入不变环区.