-
数字图像具有丰富的用户信息与直观的表达能力,是多媒体技术中常用的介质,给用户的生活带来了极大的方便[1-2].但是,图像信息主要是借助开放的网络来传输,在传输过程中易遭遇攻击,导致信息泄露、篡改,给用户带来极大的安全隐患,因此如何避免图像受到网络攻击,使其安全传输至接收端,已经是当前各国学者研究的热点[3-4].较为主流的加密技术是采用置乱-扩散的加密结构,如Liu等人[5]提出了一种基于超混沌系统与动态S盒的图像加密技术,其加密密文能够有效抵御统计攻击. Ye等人[6]提出了一种基于波线置换和块扩散的混沌图像加密算法,实验数据验证了其算法的合理性与优异性.李凯佳等人[7]提出了一种基于DNA-记忆元胞自动机与Hash函数的图像加密算法,实验结果验证了其算法的实用性.但是,此类加密技术主要是在一个方向上对像素进行扩散,且在每一轮加密期间,都是利用相同的扩散函数来改变像素值,使其密文存在周期性,导致算法的安全性不够高.
为了在消除周期性的同时提高算法的安全性与抗攻击能力,本文提出了一种基于8方向折叠机制与像素自更新置乱技术的图像加密算法.首先,基于像素自更新置乱技术来高度置乱图像像素位置,兼顾其置乱度与抗明文攻击能力;然后,借助明文尺寸来生成Logistic映射的初始条件,通过迭代该映射的输出序列来设计8方向折叠机制,从8个方向对置乱图像进行加密,并利用不同的扩散函数来改变其像素值,充分消除密文的周期性;最后,测试所提加密算法的安全性与用户响应值.
全文HTML
-
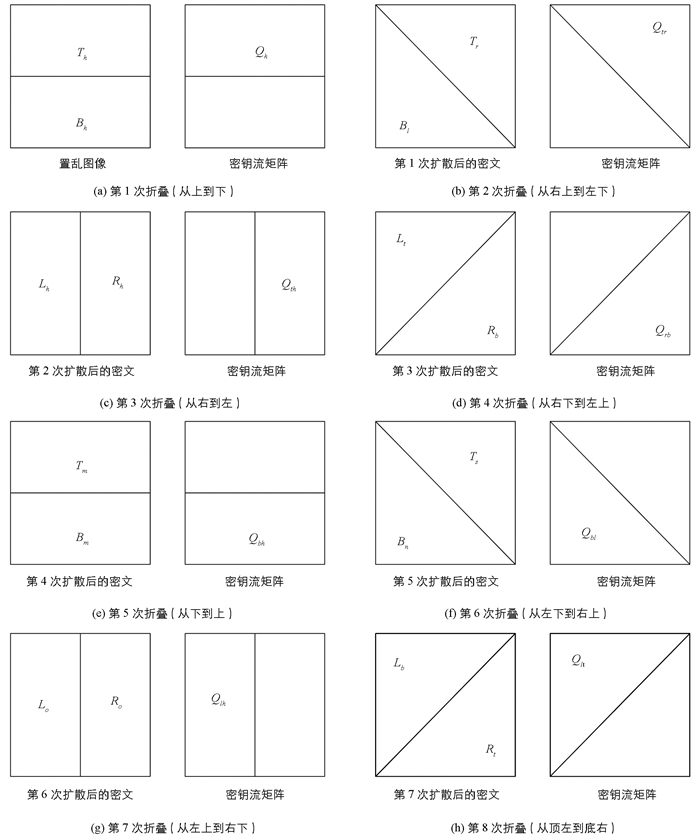
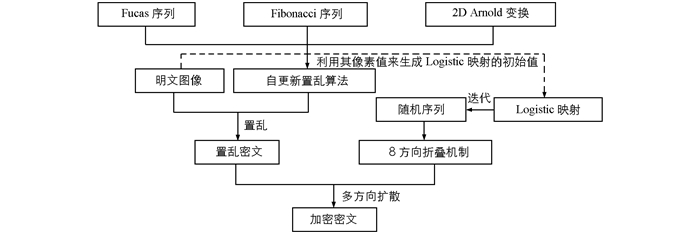
基于8方向折叠机制与像素自更新置乱技术的图像加密算法过程见图 1,它是利用不同的扩散函数从不同的方向对明文进行像素加密,避免了周期性,提高了混沌序列的随机性与密文的安全性.其主要有2个步骤:①基于像素自更新置乱技术的明文混淆;②基于8方向折叠机制的像素加密.
-
当前的图像加密思路是先变换像素位置,再改变像素值,从而实现明文的双重加密.但是,当前的加密技术所采用的像素置乱方法为周期性置乱,在多轮置乱过程中,始终使用同一个置乱操作来混淆,使其密文存在显著的周期性,降低了密文的安全性[8].对此,本文利用Fibonacci序列[9]与Lucas序列[10],构建一种自更新置乱算法,完成像素的动态混淆,充分提高明文的置乱度.标准的Fibonacci序列的初始种子仅有[(0,1),(1,1)].它是通过选择合适的种子[(0,1),(1,1)],根据循环次数的变化来实时更新其输出的整数序列,其函数分别为[9]
综合式(1)、(2)可知,在确定好种子后,随着n的变化,其对应的Fn值是截然不同的.
标准的Lucas序列和Fibonacci序列具有同样的性质,其初始种子为(2,1),相应的函数为[10]
随着n的变化,其对应的Ln值也相应地变化.
依据Fibonacci、Lucas序列的动态特性,使其满足加密技术的动态性与随机性[11].本文充分结合Fibonacci,Lucas序列,利用2D Arnold变换[12],设计了像素自更新置乱算法:
其中,(x,y)为初始明文的像素位置;(x′,y′)是处理后的像素坐标;Fn,Ln分别代表Fibonacci,Lucas序列值;N为图像宽度.
通过对比式(2)、式(3),可以发现Lucas序列与种子(1,1)的Fibonacci序列之间有如下关系:
根据标准的Lucas序列与Fibonacci序列的性质,为了满足式(5),提高所提算法的随机性与安全性,本文取Fibonacci序列的种子为(1,1),Lucas序列的种子为(2,1).
因此,式(4)可变换为
由式(6)可知,在对明文进行多轮混淆时,随着混淆次数n的增加,使得Fn,Fn+1,Fn-1,Fn+2的值出现巨大差异,导致变换核
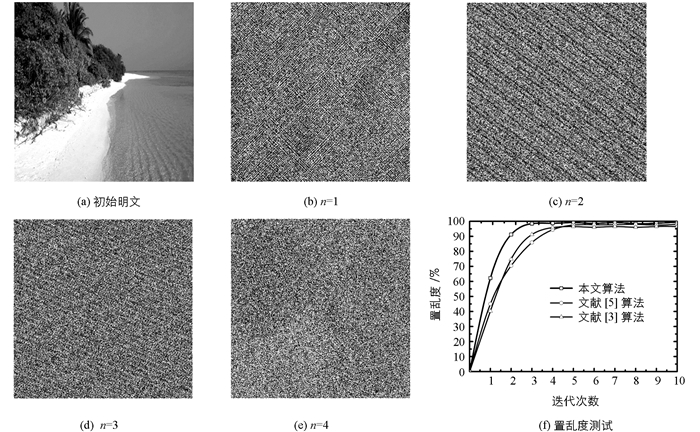
$\left[\begin{align} &{{F}_{n}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{F}_{n+1}} \\ &{{F}_{n}}+{{F}_{n-2}}~\ \ \ \ \ \ {{F}_{n+1}}+{{F}_{n-1}} \\ \end{align} \right]~$ 随着n的不同而变化.也就是在对明文进行多轮置乱时,本文像素自更新置乱算法是利用不同的混淆函数来实现像素置乱,显著改善了置乱度.为了测试所提的像素自更新置乱算法的优异性,本文以图 2(a)为样本,利用式(6)对其进行4次混淆,所获取的置乱密文见图 2(b)~2(e).根据输出的结果可知,每一轮置乱所获取的密文是不同的,也就是相邻两次混淆之间的相关性较低,避免了周期性,明文的像素被充分置乱.
为了量化其置乱度,选择文献[3]、文献[5]作为对照组,利用这3种算法的置乱技术对图 2(a)完成混淆,并基于文献[13]的方法来计算像素置乱度,
其中,R′为置乱图像;R为明文;M×N为明文尺寸.
3种技术对图 2(a)的置乱度见图 2(f).由测试结果可知,本文像素自更新置乱算法的置乱度最高,经过3轮混淆后,其置乱度达到稳定值,为99.37%,这表明明文像素被高度置乱,而文献[3]、文献[5]算法的置乱度都要小于本文所提算法,分别为95.19%、98.26%.原因是本文像素自更新置乱算法充分结合了Fibonacci序列、Lucas序列的动态特点,对于不同的迭代次数,其置乱核是不同的,有效地削弱了置乱周期性,继而改善了像素置乱度,而文献[3]、文献[5]算法是采用相同的置乱方法来进行每一轮像素混淆,使得相邻2次置乱密文之间存在一定的联系,周期性明显,降低了像素的置乱度.
-
明文经过像素置乱后,虽然其信息得到了隐藏,但是像素值并未变化,导致其安全性较低[2].为此,本文设计了一种基于8方向折叠机制的像素扩散算法,从不同的方向、利用不同的扩散函数来实现加密.首先,引入Logistic映射来获取随机序列,其模型为[14]
其中,λ∈[0, 4]是混沌性能的控制参数;xi是系统变量.
为了增强加密算法与明文之间的联系,提高其抗明文攻击能力,本文利用明文像素与外部密钥来设置式(8)的初始值x0.先将128位外部密钥K分割为8位子密钥ki,则
依据式(9)与明文像素,则初始值x0为
其中,σ为明文像素均值;t为用户设置的常量;
再选择λ,结合x0,对式(8)进行M×N次迭代,输出混沌序列x={x1,x2,…,xM×N}.利用{xi}来建立量化机制,获取密钥流{ki},则
随后,根据密钥流{ki},设计基于8方向折叠机制的扩散算法,具体步骤如下所示:
① 将尺寸为M×N的置乱密文I′的像素用矩阵R表示;同时,把密钥流{ki}用矩阵Q表示.对于第1个方向的像素扩散,其过程见图 3(a),扩散函数为
其中,Th(i,j)、Bh(N-i+1,j)分别是矩阵R上半部分中(i,j)、下半部分中(N-i+1,j)对应的像素值;Qh(i,j)是矩阵Q上半部分中(i,j)对应的密钥流;T′h(i,j)、B′h(N-i+1,j)分别是Th(i,j)、Bh(N-i+1,j)扩散后的像素值.
② 经过步骤①的扩散后,输出第一个密文I1′;再根据密文I1′,进行第2个方向的像素加密,其过程见图 3(b),扩散函数为
其中,Tr(i,j)是密文I1′右上半部分中(i,j)对应的像素值;Bl(j,i)是密文I′左下部分与(i,j)关于对角线对称位置的像素值;Qtr(i,j)是矩阵Q右上部分中(i,j)对应的密钥流;T′r(i,j)、B′l(j,i)分别是Th(i,j)、Bh(j,i)扩散后的像素值.
③ 经过步骤②的扩散后,输出第2个密文I2′;再根据密文I2′,进行第3个方向的像素加密,其过程见图 3(c),扩散函数为
其中,Rh(i,N-j+1)、Lh(i,j)分别是密文I2′右半部分中(i,N-j+1)、左半部分中(i,j)对应的像素值;Qtr(i,j)是矩阵Q右半部分中(i,j)对应的密钥流;R′h(i,N-j+1)、L′h(i,j)分别是Rh(i,N-j+1)、Lh(i,j)扩散后的像素值.
④ 经过步骤③的扩散后,输出第3个密文I3′;再根据密文I3′,进行第4个方向的像素加密,其过程见图 3(d),扩散函数为
其中,Rb(i,j)是密文I3′右下部分中(i,j)对应的像素值;Lt(i-1,j-1)是密文I′3左上部分中(i-1,j-1)对应的像素值;Qrb(i,j)是矩阵Q右下半部分中(i,j)对应的密钥流;R′b(i,j)、L′t(i-1,j-1)分别是Rb(i,j)、Lt(i-1,j-1)扩散后的像素值.
⑤ 经过步骤④的扩散后,输出第4个密文I4′;再根据密文I4′,进行第5个方向的像素加密,其过程见图 3(e),扩散函数为
其中,Bm(i,j)是密文I4′下半部分中(i,j)对应的像素值;Tm(N-i+1,j)是密文I′4上半部分中(N-i+1,j)对应的像素值;Qbh(i,j)是矩阵Q下半部分中(i,j)对应的密钥流;B′m(i,j)、T′m(N-i+1,j)分别是Bm(i,j)、Tm(N-i+1,j)扩散后的像素值.
⑥ 经过步骤⑤的扩散后,输出第5个密文I5′;再根据密文I5′,进行第6个方向的像素加密,其过程见图 3(f),扩散函数为
其中,Bn(i,j)是密文I5′左下部分中(i,j)对应的像素值;Ts(j,i)是密文I′5右上部分与(i,j)关于对角线对称位置的像素值;Qbl(i,j)是矩阵Q左下部分中(i,j)对应的密钥流;B′n(i,j)、T′s(j,i)分别是Bn(i,j)、Ts(j,i)扩散后的像素值.
⑦ 经过步骤⑥的扩散后,输出第6个密文I6′;再根据密文I6′,进行第7个方向的像素加密,其过程见图 3(g),扩散函数为
其中,Lo(i,j)是密文I6′左半部分中(i,j)对应的像素值;Ro(i,N-j+1)是密文I′6右半部分中(i,N-j+1)对应的像素值;Qlh(i,j)是矩阵Q左半部分中(i,j)对应的密钥流;L′o(i,j)、R′o(i,N-j+1)分别是Lo(i,j)、Ro(i,N-j+1)扩散后的像素值.
⑧ 经过步骤⑦的扩散后,输出第7个密文I7′;再根据密文I7′,进行第8个方向的像素加密,其过程见图 3(h),扩散函数为
其中,Lb(i,j)是密文I7′左上部分中(i,j)对应的像素值;Rt(i+1,j+1)是密文I′7右下部分中(i+1,j+1)对应的像素值;Qlt(i,j)是矩阵Q左上部分中(i,j)对应的密钥流;L′b(i,j)、R′t(i+1,j+1)分别是Lb(i,j)、Rt(i+1,j+1)扩散后的像素值.
经过第8个方向的扩散处理后,输出最终的密文I8′.以图 2(d)为目标,利用本文设计的8方向折叠机制对其进行扩散加密,输出的密文见图 4.依图可知,经过8个方向的像素扩散后,每个方向的输出密文均与置乱图像是截然不同的,图像信息的隐密度进一步提高,抗攻击能力更强.
本文引入信息熵值[7]来量化每个方向输出密文的安全性能,它是衡量图像信息不确定性的理想指标.因图像数据量大,且其像素间的相关性较高,因此,未经加密的图像其熵值较小,而经过加密后的图像其熵值很大.当值越靠近8时,显示其不确定性越高,密文安全性也就越高[15].信息熵值计算函数为[15]
其中,xi是图像中第i个像素的灰度值;L∈[0, 256]为图像灰度等级;P(xi)为第i个像素的灰度值在整个图像中所占的比例,且
依据式(20),利用文献[15]的计算过程,得到图 8(a)~8(b)的熵值见表 1,由表可知,随着方向个数的增加,其扩散效果越来越好.经过第8次扩散后,其密文熵值约为7.997 6,与理论值8非常接近.这表明对明文进行多个方向扩散,能够显著提高密文的安全性.为此,本文将方向数量设置为8进行加密实验.
1.1. 基于像素自更新置乱算法的明文混淆
1.2. 基于8方向折叠机制的像素扩散
-
为了验证所提加密算法的安全性与抗攻击能力,本文在Matlab平台上进行测试,另外,将当前安全度较高的加密技术作为对照组:文献[18]、文献[5]、文献[7].其中,文献[18]为光学加密技术,通过利用不同的混沌映射来生成所需要的随机模板来实现图像加密.而文献[5]、文献[7]则是采用了置乱-扩散的混沌加密结构.算法关键参数为:初始种子为(1,1),λ=3.35,外部密钥K=10yhg65ewmaz91bx,t=2.
-
把图 5(a)作为加密实验的样本,4种加密算法结果分别见图 5(b)~5(e).由测试结果可知,本文算法与文献[18]、文献[5]、文献[7]算法的加密效果都较为理想,初始图像的信息均被充分隐藏,明文内容被高度混淆,没有视觉信息泄露.为了区分4种加密算法的安全性,本文再次利用信息熵值[7]来量化,得到的熵值见表 2.由表 2可知,本文算法的密文熵值最大,达到了7.998 4,与理论值8的偏差非常小,这显示其安全性最高,而文献[5]、文献[7]、文献[18]算法的密文熵值均要低于所提算法,分别为7.992 6,7.989 5,7.981 4,这表明三者的安全性不佳.尤其是文献[18],虽然该算法能够充分隐藏明文信息,但是存在一定的轮廓效应,见图 5(e).原因是本文加密机制充分结合了Lucas、Fibonacci序列的动态性,采用了像素自更新技术,在每一轮像素置乱过程中,利用不同的置乱核来混淆像素位置,有效降低了置乱周期性,同时,利用明文像素与外部密钥来生成密钥流,采用了8方向折叠机制,从8个方向利用8个不同的扩散函数来改变像素值,避免了像素扩散的周期性,显著提高了密文的安全性与抗攻击能力;而文献[5]虽然采用了高维混沌系统,通过牺牲算法的效率来提高密文安全性,而且通过设计动态S盒来充分改变像素值,提高了算法的动态性与随机性,但是该算法在置乱与扩散过程中,都是采用相同的加密操作来获取密文,导致其密文存在显著的周期性特点,继而削弱了算法的安全性,且整个加密机制忽略了明文自身特性,使其抗明文攻击能力较弱;文献[7]通过将时间延迟思想引入低维混沌映射中,降低序列的自相关性,而且利用记忆元胞自动机来实现像素扩散,但是此算法是从一个方向来实现像素扩散,且在每一轮加密过程中,都是采用相同的置乱与扩散机制来改变像素位置与像素值,使得明文内容的混淆程度不佳,从而导致密文的安全性较弱.文献[18]虽然结合了混沌理论与光学技术来快速加密图像,其实质为光学干涉加密,明文通过光学加密装置后,将明文的所有信息集中在一个纯相位掩码中,使其存在轮廓显现问题,导致密文安全性不理想.
-
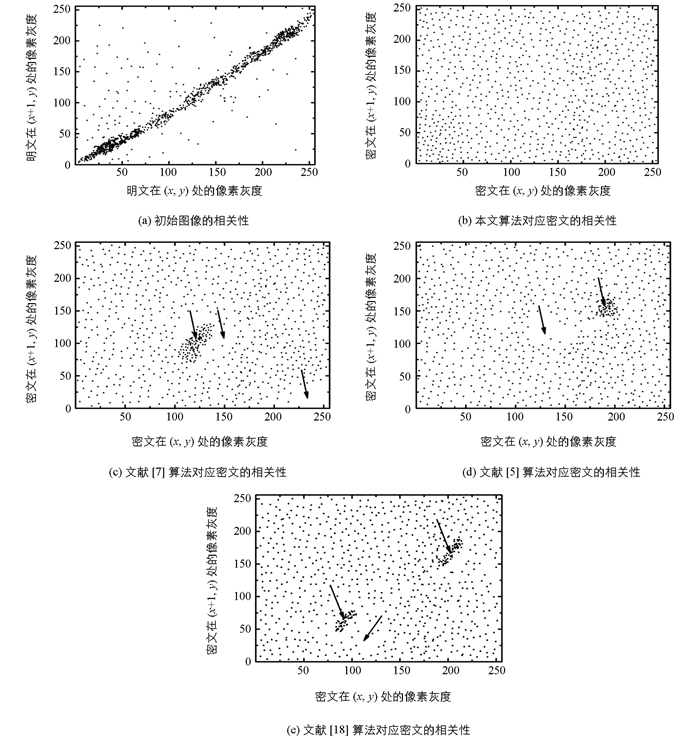
图像相邻两像素之间的相关性对密文安全性有较大威胁,攻击者通常利用像素间的相关性破译密文,故数字图像加密技术应该要最大程度地降低这种相关性[3].为了测试输出密文的相关性,本文从图 5(b)~5(e) 4幅密文中选择2 500对相邻像素点来验证其相关性,相关性用相关系数Cxy来表示,Cxy值越大相关性越大,其模型为[7]
各算法的密文在X方向上的相关性测试结果见图 6.由图 6(a)可知,初始图像的像素相关系数很高,像素分布极为不均,其Cxy值约为0.961 8;然而,初始明文被4种算法加密后,明文的相关性被显著降低,输出密文的像素分布变得均匀,其Cxy值分别为0.003 1,0.006 8,0.004 9,0.007 5.本文所提算法输出密文的像素分布均匀性最好,没有堆积现象,其分布均匀性要优于其他3种算法,见图 6(b)~6(e).
各密文在另外2个方向上的Cxy计算数据如表 3所示.由表 3可知,初始图像的Cxy值是最大的,表明其相关性最大.但是,明文经过4种加密算法处理后,图像的Cxy值被显著降低,且本文所提算法的Cxy值是最小的,要远低于其他3种加密算法.
-
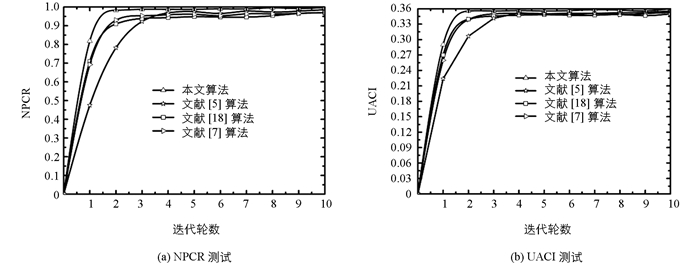
在国内外研究中,NPCR与UACI曲线是衡量加密算法抗明文攻击能力的有效指标[15].故本文基于文献[16]的方法,验证4种算法的NPCR与UACI曲线,结果见图 7.在这4种加密方案中,本文所提加密算法具有更高的NPCR与UACI均值,分别为99.79%,34.52%,而文献[5]、文献[7]、文献[18]的NPCR与UACI均值都要略小于本文算法,尤其是文献[18],其NPCR与UACI均值最小.这表明本文加密算法的抗明文攻击能力最好,原因是所提加密机制利用明文像素来生成一组密钥流,并以此设计了8方向折叠机制来改变像素值,使得在8个不同方向的像素扩散中,均考虑了明文像素,从而增强了抗明文攻击的能力.文献[5]利用高维混沌系统来加密明文,在一定程度上提高了密文的安全性,但是其置乱与扩散过程均与明文无关,导致其抗明文攻击能力要低于本文所提算法;文献[7]与本文算法一样,借助低维混沌映射来置乱与扩散,虽然利用了DNA编码技术,但DNA编码技术也是脱离了明文,从而导致其抗明文攻击能力较弱.文献[18]虽然采用了光学装置来实现加密,但是它将明文的所有信息集中在一个纯相位掩码中,存在轮廓显现问题,且其加密过程忽视了明文特性,从而使其安全性最低,导致其抗明文攻击能力不理想.
-
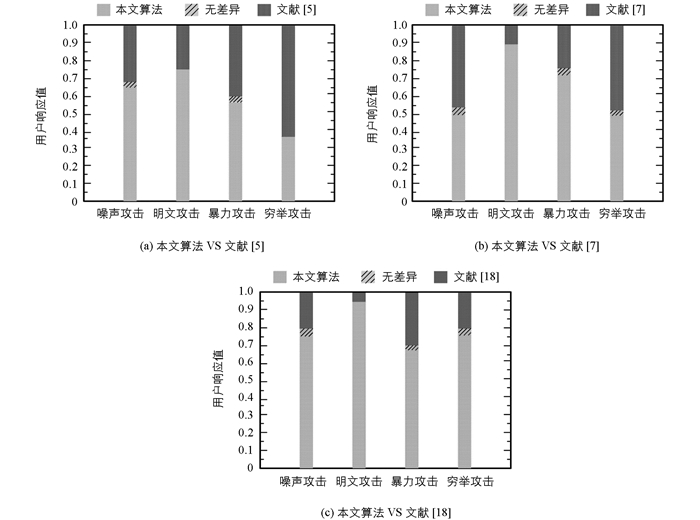
用户响应是评估加密算法在市场上受欢迎程度的重要参考指标,故本文利用Amazon Mechanical Turk[17]来验证这4种算法的用户响应值.根据图像在网络中常遇到的攻击类型,将噪声、明文、暴力与穷举攻击[7]作为本次实验的对象,不同攻击类型下各算法的响应值见图 8.
根据响应结果可知,面对噪声、暴力以及明文攻击时,所提算法的用户响应程度更高,但是,在面对穷举攻击时,文献[5]的算法使用了高维混沌系统与动态S盒来实现加密,显著增大了算法的密钥空间,使其响应度最高.
2.1. 加密质量对比分析
2.2. 密文相邻像素间的相关性测试
2.3. 抗明文攻击能力对比测试
2.4. 用户响应对比测试
-
为了从多个方向对明文进行扩散,且能有效消除周期性,本文提出了一种基于8方向折叠机制与自更新置乱的图像加密算法.利用Lucas、Fibonacci序列设计了一种像素自更新置乱算法,有效地降低了混淆周期性,进一步提高了明文像素的置乱度;利用明文与外部密钥来生成Logistic映射初值,利用量化机制来获取密钥流,从而设计了8方向折叠机制,从8个方向对置乱图像进行高度加密.实验结果验证了所提算法的安全性与抗攻击能力.



 下载:
下载: